Trapecio (Geometría)

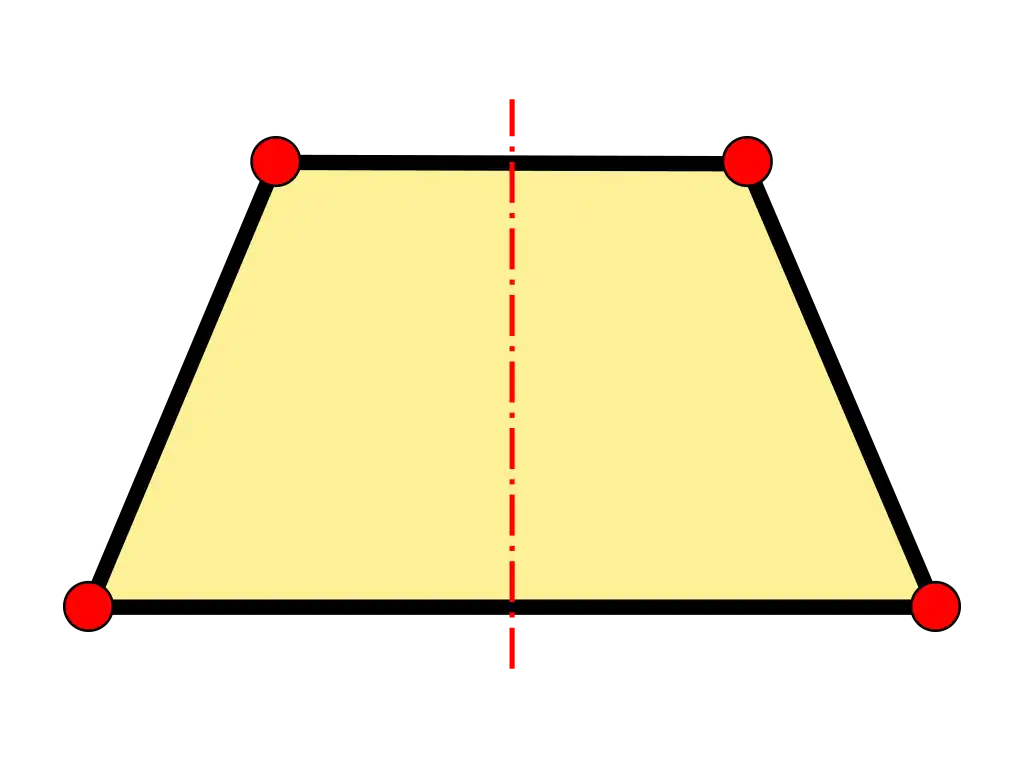
format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En geometría se denomina Trapecio a un cuadrilátero que tiene solo un par de lados paralelos.

Los trapecios tienen cuatro lados, dos paralelos y dos no paralelos. Los lados paralelos se denominan bases, y los no paralelos se denominan laterales o catetos.

Por tener cuatro lados los tapecios son cuadriláteros convexos, y sus ángulos internos deben sumar siempre 360°. No debe confundirse el trapecio con el trapezoide, que no tiene ninguno de sus lados paralelos entre sí, ni tampoco debe confundirse con los paralelogramos (rombos y romboides) que tienen todos su lados paralelos entre sí.

A diferencia del resto de cuadriláteras, el trapecio se distingue precisamente por mantener esta estructura de dos lados paralelos y dos no paralelos, independientemente de la longitud de sus lados o de la amplitud de sus ángulos. La presencia de solo un par de lados paralelos le otorga al trapecio una amplia diversidad de formas, que se clasifican según la longitud y orientación de sus lados.

Existen tres categorías principales de trapecios, cada una con características distintivas:

Trapecio Escaleno: ninguno de sus lados es igual a otro, presentando una asimetría total en sus dimensiones.
Trapecio Isósceles: los lados no paralelos o laterales son de igual longitud, aunque se extienden en direcciones opuestas, otorgándole una simetría particular.
Trapecio Rectángulo: uno de sus lados no paralelos es perpendicular a las bases, formando un ángulo recto.

En resumen, el trapecio es una figura geométrica de cuatro lados, que se define por su configuración de lados paralelos y no paralelos. Esta definición le confiere gran variedad de formas y propiedades, permitiendo su clasificación en diferentes tipos según las dimensiones y orientación de sus lados.

Clasificación de los trapecios

Trapecios según sus ángulos — 1. rectángulo
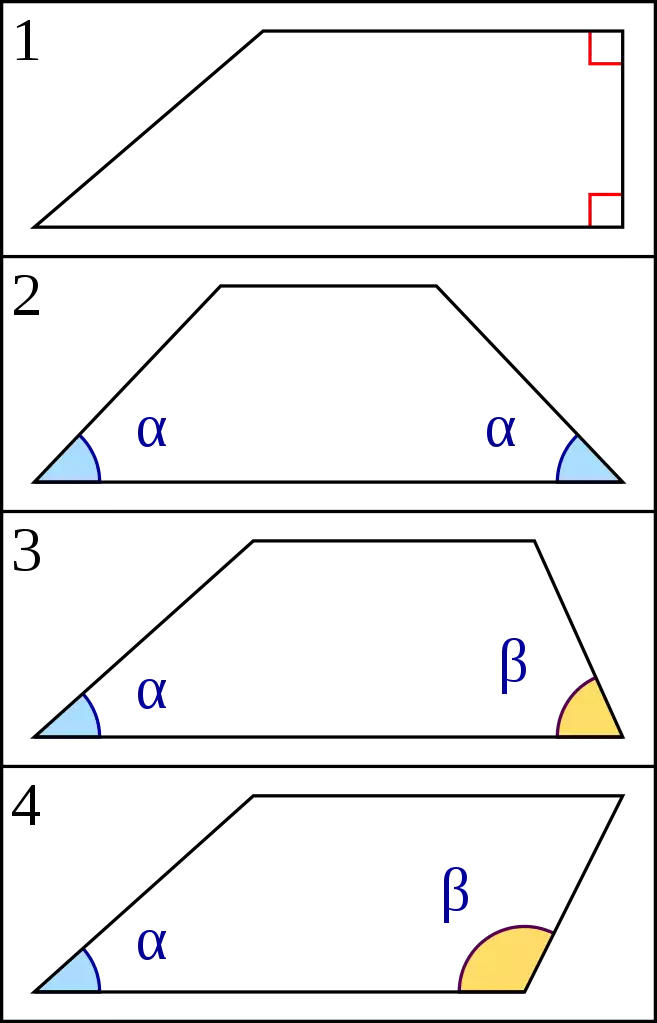
2. isósceles
3. escaleno agudo
4. escaleno obtuso

Los trapecios se pueden clasificar de diversas maneras, aunque suele hacerse según la clasificación más básica propuesta por Euclides, quien los dividió en tres tipos según la apertura de sus ángulos:

Rectángulos
Isósceles
Escalenos

Trapecios Rectángulos: Un trapecio rectángulo tiene dos ángulos rectos adyacentes, lo que significa que uno de sus lados es perpendicular a ambas bases. Estos trapecios son esenciales en la regla trapezoidal para estimar áreas bajo una curva.

Trapecio Isósceles: Estos trapecios tienen ángulos de igual medida en cada base. Como resultado, ambos lados también son de igual longitud y son simétricos entre sí. Si la longitud de una de las bases es igual a la de los lados, se le denomina trapecio trisolátero.

Trapecio Escalenos: Estos trapecios tienen lados que no son iguales entre sí y no poseen ángulos rectos. Aunque Euclides no los clasificó, pueden encontrarse de dos tipos según la apertura del segundo ángulo de una de sus bases:

Trapecio escaleno agudos: los ángulos de una base son todos agudos.
Trapecio escaleno obtusos: tienen un ángulo agudo y otro obtuso en cada base.

Esta clasificación de Euclides sirve como referencia básica para comprender y diferenciar las diferencias formas que puede tomar un trapecio, y para poder trabajar más eficientemente con ellas en el espacio geométrico, debido a sus características particulares.

Historia de los trapecios

El matemático griego Euclides clasificó cinco cuadriláteros, cuatro de los cuales tenían dos pares de lados paralelos: cuadrado, rectángulo, rombo y romboide, mientras el último, denominado trapecio (τραπέζια) solo tenía un par de lados paralelos. Su nombre proviene del griego τετράς (tetrás), que significa "cuatro", y πέζα (péza), que se traduce como "pie" o "borde".

Proclo (412 a 485 d. C.) en su comentario sobre los Elementos de Euclides, diferenció dos tipos de trapecio:

Con un par de lados paralelos, subdividido en trapecios isósceles (patas iguales) y escalenos (desiguales).
Sin lados paralelos, denominado trapezoide (τραπεζοειδή, trapezoeidé), que significa "similar a un trapecio".

La mayoría de los idiomas europeos adoptaron la estructura de Proclo. Sin embargo, un diccionario matemático de Charles Hutton en 1795 cambió la terminología en inglés. Aunque este error se corrigió en el inglés británico hacia 1875, persiste en el inglés americano.

Un paralelogramo es un cuadrilátero similar al trapecio, pero con dos pares de lados paralelos y tiene simetría rotacional central de 2 pliegues. Esta simetría también es posible en trapecios obtusos o trapezoides rectos (rectángulos).

Un trapezoide tangencial es aquel que tiene una circunferencia inscrita. En geometría hiperbólica, un cuadrilátero de Saccheri se asemeja a un trapezoide con dos ángulos rectos adyacentes, mientras que en geometría euclidiana es un rectángulo. Un cuadrilátero de Lambert en geometría hiperbólica tiene tres ángulos rectos.

Este artículo utiliza el término trapezoide propia del mundo hispano, aunque en Estados Unidos y Canadá a menudo se refieren al trapezoide como cuadrilátero irregular.

Diferencia entre trapecio y trapezoide

En español, los términos trapecio y trapezoide se usan para dos figuras geométricas diferentes, aunque por influencia del inglés estadounidense, en los últimos años ha ganado popularidad el uso indistinto de ambos términos.

Trapecio: cuadrilátero con al menos un par de lados paralelos.
Trapezoide: cuadrilátero sin lados paralelos.

El término "trapecio" (trapezium) se usa para referirse a un cuadrilátero con solo un par de lados paralelos, mientras que el término "trapezoide" (trapezoid) se usa para referirse a un cuadrilátero sin ningún lado paralelos.

HSD

Definición inclusiva vs exclusiva

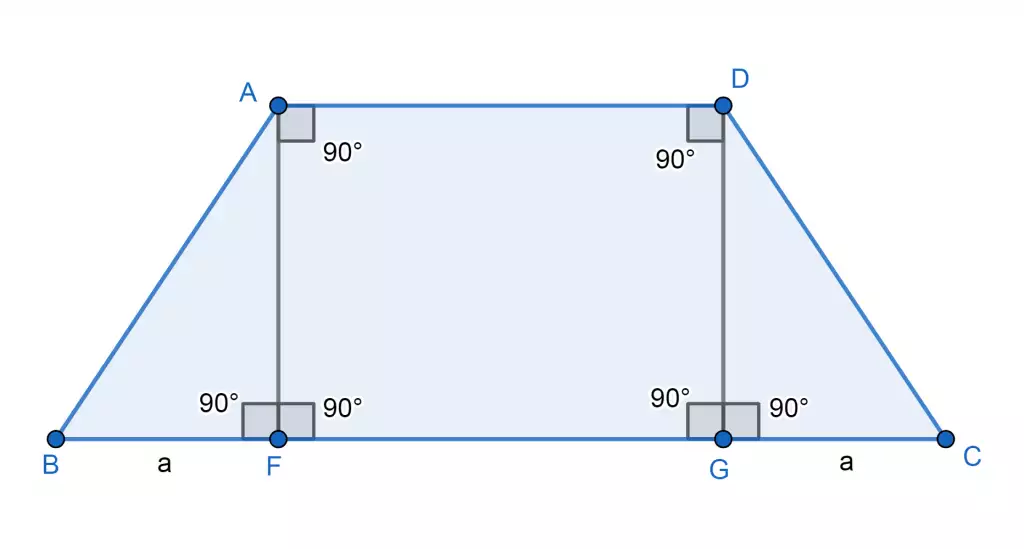
Comparación entre trapecio y cuadrado — Formación de un trapecio a partir de un cuadrado

Existe cierto desacuerdo sobre si los paralelogramos, que tienen dos pares de lados paralelos, deben considerarse trapezoides. Algunos definen un trapezoide como un cuadrilátero que tiene solo un par de lados paralelos (la definición exclusiva), excluyendo así los paralelogramos. Otros definen un trapezoide como un cuadrilátero con al menos un par de lados paralelos (la definición inclusiva ), lo que hace que el paralelogramo sea un tipo especial de trapezoide. La última definición es consistente con sus usos en matemáticas superiores como el cálculo. Este artículo usa la definición inclusiva y considera los paralelogramos como casos especiales de un trapezoide. Esto también se recomienda en la taxonomía de los cuadriláteros.

Según la definición inclusiva, todos los paralelogramos (incluidos los rombos, los rectángulos y los cuadrados) son trapezoides. Los rectángulos tienen simetría de espejo en los bordes medios; los rombos tienen simetría especular en los vértices, mientras que los cuadrados tienen simetría especular tanto en los bordes medios como en los vértices.

Características del trapecio

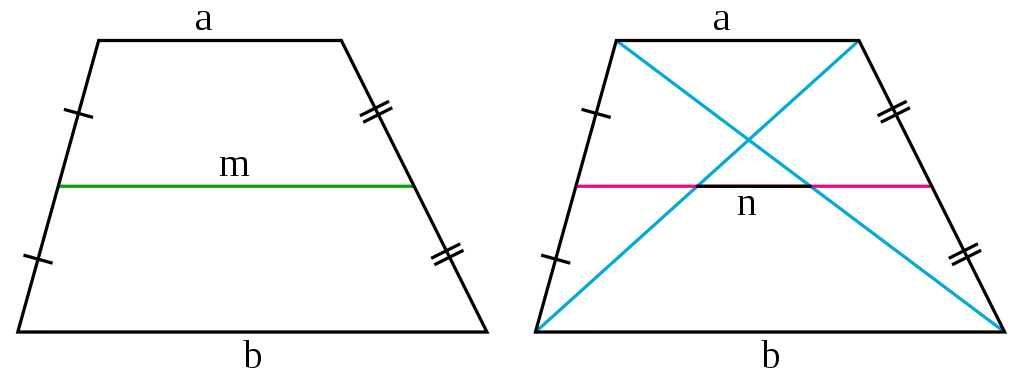
Dado un cuadrilátero convexo, las siguientes propiedades son equivalentes y cada una implica que el cuadrilátero es un trapezoide:

Tiene dos ángulos adyacentes que son suplementarios, es decir, suman 180 grados.
El ángulo entre un lado y una diagonal es igual al ángulo entre el lado opuesto y la misma diagonal.
Las diagonales se cortan mutuamente en la misma proporción (esta proporción es la misma que entre las longitudes de los lados paralelos).
Las diagonales cortan el cuadrilátero en cuatro triángulos de los cuales un par opuesto tiene áreas iguales.
El producto de las áreas de los dos triángulos formados por una diagonal es igual al producto de las áreas de los dos triángulos formados por la otra diagonal.
Las áreas S y T de unos dos triángulos opuestos de los cuatro triángulos formados por las diagonales satisfacen la ecuación

$\sqrt{K}=\sqrt{S}+\sqrt{T},$ donde K es el área del cuadrilátero.

Los puntos medios de dos lados opuestos y la intersección de las diagonales son colineales.
Los ángulos en el cuadrilátero ABCD satisfacen
$\sen A\sen C=\sen B\sen D.$
Los cosenos de dos ángulos adyacentes suman 0, al igual que los cosenos de los otros dos ángulos.
Las cotangentes de dos ángulos adyacentes suman 0, al igual que las cotangentes de los otros dos ángulos adyacentes.
Una bimediana divide el cuadrilátero en dos cuadriláteros de áreas iguales.
El doble de la longitud de la bimediana que une los puntos medios de dos lados opuestos es igual a la suma de las longitudes de los otros lados.

Además, las siguientes propiedades son equivalentes y cada una implica que los lados opuestos a y b son paralelos:

Los lados consecutivos a, c, b, d y las diagonales p, q satisfacen la ecuación

$p^2+q^2=c^2+d^2+2ab.$

La distancia v entre los puntos medios de las diagonales satisface la ecuación

$v=\frac{|ab|}{2}.$

Propiedades del trapecio

Condiciones de existencia

Cuatro longitudes a, c, b, d pueden constituir los lados consecutivos de un trapezoide sin paralelogramo con a y b paralelos solo cuando

El cuadrilátero es un paralelogramo cuando ${\ estilo de visualización dc = ba = 0}$ , pero es un cuadrilátero ex-tangencial (que no es un trapezoide) cuando $|dc|=|ba|\neq 0$ .

Segmento medio y altura

El segmento medio (también llamado mediana o línea media) de un trapezoide es el segmento que une los puntos medios de los catetos. Es paralelo a las bases. Su longitud m es igual a la media de las longitudes de las bases a y b del trapezoide, $m = \frac{a + b}{2}.$

El segmento medio de un trapezoide es una de las dos bimedianas (la otra bimediana divide el trapezoide en áreas iguales).

La altura (o altitud) es la distancia perpendicular entre las bases. En el caso de que las dos bases tengan longitudes diferentes ( a ≠ b ), la altura de un trapezoide h se puede determinar por la longitud de sus cuatro lados usando la fórmula

$h= \frac{\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+cd)(ab-c+d)}}{2|ba|}$

donde c y d son las longitudes de los catetos.

Área del trapecio

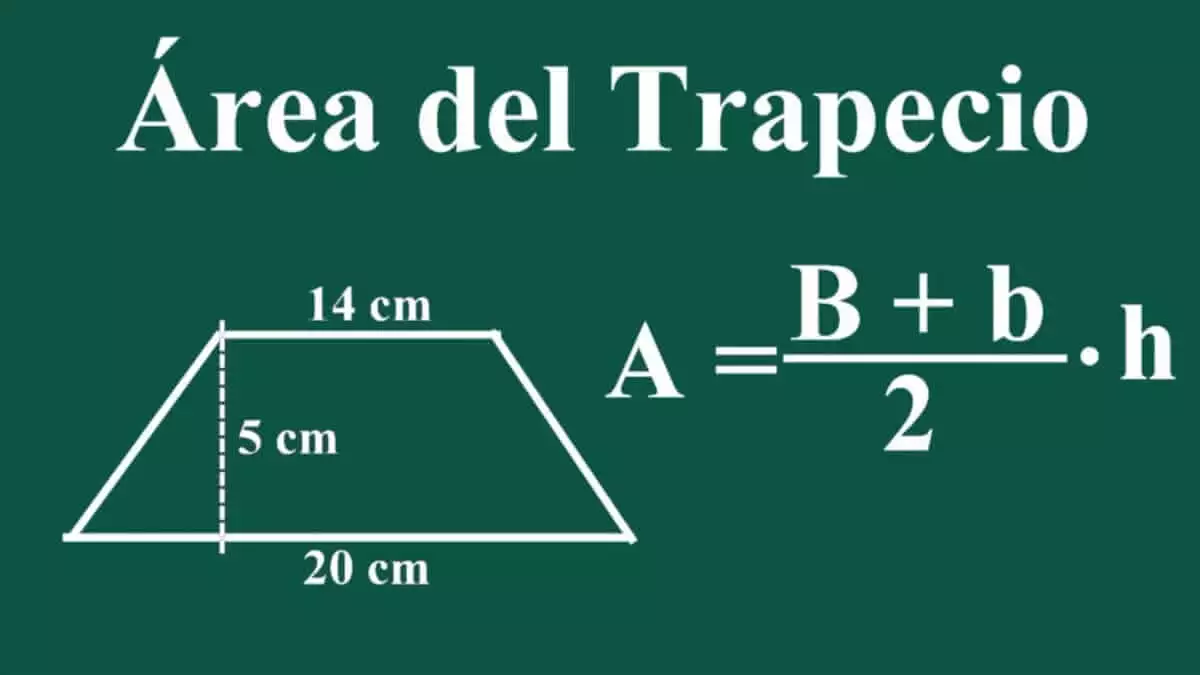
El área K de un trapezoide está dada por

$K = \frac{a + b}{2} \cdot h = mh$

donde a y b son las longitudes de los lados paralelos, h es la altura (la distancia perpendicular entre estos lados) y m es la media aritmética de las longitudes de los dos lados paralelos. En el año 499 d. C., Aryabhata, un gran matemático y astrónomo de la época clásica de las matemáticas y la astronomía indias, utilizó este método en el Aryabhatiya (sección 2.8). Esto produce como caso especial la conocida fórmula para el área de un triángulo, al considerar un triángulo como un trapezoide degenerado en el que uno de los lados paralelos se ha reducido a un punto.

El matemático indio del siglo VII Bhāskara I derivó la siguiente fórmula para el área de un trapezoide con lados consecutivos a, c, b, d :

$K={\frac {1}{2}}(a+b){\sqrt {c^{2}-{\frac {1}{4}}\left((ba)+{\frac {c^{2}-d^{2}}{ba}}\right)^{2}}}$

donde a y b son paralelos y b > a. Esta fórmula se puede factorizar en una versión más simétrica

$K = \frac{a+b}{4|ba|}\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+cd)(ab-c+d )}.$

Cuando uno de los lados paralelos se ha reducido a un punto (digamos a = 0), esta fórmula se reduce a la fórmula de Heron para el área de un triángulo.

Otra fórmula equivalente para el área, que se asemeja más a la fórmula de Heron, es

$K = \frac{a+b}{|ba|}\sqrt{(sb)(sa)(sbc)(sbd)},$

donde (a+b+c+d)} $s = \tfrac{1}{2}(a + b + c + d)$ es el semiperímetro del trapezoide. (Esta fórmula es similar a la fórmula de Brahmagupta, pero se diferencia de ella en que un trapezoide podría no ser cíclico (inscrito en un círculo). La fórmula también es un caso especial de la fórmula de Bretschneider para un cuadrilátero general).

De la fórmula de Bretschneider se sigue que

$K= \sqrt{\frac{(ab^2-a^2 b-ad^2+bc^2)(ab^2-a^2 b-ac^2+bd^2)}{(2(ba ))^2} - \left(\frac{b^2+d^2-a^2-c^2}{4}\right)^2}.$

La línea que une los puntos medios de los lados paralelos, biseca el área.

Diagonales

Las longitudes de las diagonales son

$p= \sqrt{\frac{ab^2-a^2b-ac^2+bd^2}{ba}},$

$q= \sqrt{\frac{ab^2-a^2b-ad^2+bc^2}{ba}}$

donde a es la base corta, b es la base larga y c y d son los catetos trapezoidales.

Si el trapecio se divide en cuatro triángulos por sus diagonales AC y BD (como se muestra a la derecha), que se cortan en O, entonces el área de $\triángulo$ AOD es igual a la de $\triángulo$ BOC, y el producto de las áreas de $\triángulo$ AOD y $\triángulo$ BOC es igual al de $\triángulo$ AOB y $\triángulo$ DQO _ La razón de las áreas de cada par de triángulos adyacentes es la misma que entre las longitudes de los lados paralelos.

Sea el trapezoide con vértices A, B, C y D en secuencia y con lados paralelos AB y DC. Sea E la intersección de las diagonales, y sea F del lado DA y G del lado BC tal que FEG es paralela a AB y CD. Entonces FG es la media armónica de AB y DC :

$\frac{1}{FG}=\frac{1}{2} \left( \frac{1}{AB}+ \frac{1}{DC} \right).$

La línea que pasa por el punto de intersección de los lados no paralelos extendidos y el punto de intersección de las diagonales, biseca cada base.

Otras propiedades

El centro de área (centro de masa para una lámina uniforme) se encuentra a lo largo del segmento de línea que une los puntos medios de los lados paralelos, a una distancia perpendicular x del lado más largo b dada por $x = \frac{h}{3} \left( \frac{2a+b}{a+b}\right).$

El centro del área divide este segmento en la proporción (cuando se toma del lado corto al lado largo) ${\frac{a+2b}{2a+b}}.$

Si las bisectrices de los ángulos A y B se intersecan en P, y las bisectrices de los ángulos C y D se intersecan en Q, entonces $PQ=\frac{|AD+BC-AB-CD|}{2}.$

Aplicaciones

Arquitectura

En arquitectura, la palabra se usa para referirse a puertas, ventanas y edificios simétricos construidos más anchos en la base, estrechándose hacia la parte superior, en estilo egipcio. Si estos tienen lados rectos y esquinas angulares afiladas, sus formas suelen ser trapezoides isósceles. Este era el estilo estándar para las puertas y ventanas de los Incas.

Geometría

El problema de las escaleras cruzadas es el problema de encontrar la distancia entre los lados paralelos de un trapecio recto, dadas las longitudes de las diagonales y la distancia desde el cateto perpendicular hasta la intersección de la diagonal.

Biología

En morfología, taxonomía y otras disciplinas descriptivas en las que es necesario un término para tales formas, términos como trapezoidal o trapeziforme suelen ser útiles en las descripciones de órganos o formas particulares.

Ingeniería Informática

En ingeniería informática, específicamente en lógica digital y arquitectura informática, los trapecios se utilizan normalmente para simbolizar multiplexores. Los multiplexores son elementos lógicos que seleccionan entre múltiples elementos y producen una única salida basada en una señal de selección. Los diseños típicos emplearán trapezoides sin indicar específicamente que son multiplexores, ya que son universalmente equivalentes.

Contenido relacionado

Más resultados...