Espacio euclidiano

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Imágen de un espacio euclidiano — Un punto en el espacio euclidiano tridimensional ubicado mediante tres coordenadas

El espacio euclidiano es la representación geométrica del espacio físico, sobre el cual se posicionan las figuras geométricas. Este espacio constituye el plano fundamental de la geometría y está construído como un espacio vectorial real, de dimensiones finitas, dotado de un producto escalar. O en otras palabras, como un conjunto de vectores en coordenadas predecibles.

Se denomina euclidiano por haber sido planteado por la geometría de Euclides y para diferenciarlo de otros tipos de espacios que se han explorado en la física y matemáticas contemporáneas, como los espacios curvos o el espacio de la teoría de la relatividad de Einstein. Por su origen, el espacio euclidiano satisface los axiomas de Euclides.

En sus orígenes, como se describe en los Elementos de Euclides, era el espacio tridimensional de la geometría euclidiana. Sin embargo, en la matemática moderna, el concepto se ha expandido para incluir espacios euclidianos de cualquier dimensión entera positiva. Esto abarca tanto el espacio tridimensional como el plano euclidiano (de dos dimensiones).

Los antiguos matemáticos griegos fueron pioneros en usar el espacio euclidiano para transformar el espacio físico, gracias a obras como "Elementos". Euclides presentó una gran innovación: demostrar todas las propiedades del espacio como teoremas, partiendo de un conjunto limitado de postulados fundamentales. El espacio abstracto resultante es el espacio euclidiano.

Con la aparición de las geometrías no euclidianas a finales del siglo XIX, se reformularon los postulados antiguos para definir el espacio euclidiano en función de la teoría axiomática. Aunque también puede definirse en función de espacios vectoriales y álgebra lineal. Esta última es la que predomina en las matemáticas modernas. En todas sus definiciones, los espacios euclidianos se componen de puntos que se definen solo por las propiedades que deben tener para formar un espacio euclidiano.

§ Por lo tanto, en muchos casos es posible trabajar con un espacio euclidiano específico, que es generalmente el verdadero n-espacio ${displaystyle mathbb {R} ^{n},}$ equipado con el producto de punto. Un isomorfismo de un espacio euclidiano a $mathbb {R} ^{n}$ asocia con cada punto un n-tuple de números reales que ubican ese punto en el espacio Euclideano y se llaman el Coordenadas cartesianas de ese punto.

Esencialmente, existe un único espacio euclidiano por cada dimensión; es decir, todos los espacios euclidianos para una dimensión específica son isomorfos entre sí. Por lo tanto es posible trabajar con un espacio euclidiano específico, denotado como Eⁿ, que puede representarse utilizando coordenadas cartesianas como el espacio real n-dimensional ℝⁿ de producto escalar.

HSD

Definición

Historia de la definición

El espacio euclidiano fue introducido por los antiguos griegos como una abstracción de nuestro espacio físico. Su gran innovación, que apareció en los Elementos de Euclides, fue construir y probar toda la geometría a partir de unas pocas propiedades muy básicas, que se abstraen del mundo físico y no pueden probarse matemáticamente debido a la falta de herramientas más básicas. Estas propiedades se denominan postulados o axiomas en lenguaje moderno. Esta forma de definir el espacio euclidiano todavía se usa bajo el nombre de geometría sintética.

En 1637, René Descartes introdujo las coordenadas cartesianas y demostró que esto permite reducir los problemas geométricos a cálculos algebraicos con números. Esta reducción de la geometría al álgebra supuso un gran cambio de punto de vista, ya que hasta entonces los números reales se definían en términos de longitudes y distancias.

La geometría euclidiana no se aplicó en espacios de más de tres dimensiones hasta el siglo XIX. Ludwig Schläfli generalizó la geometría euclidiana a espacios de dimensión $n$ , utilizando métodos sintéticos y algebraicos, y descubrió todos los politopos regulares (superiores -análogos dimensionales de los sólidos platónicos) que existen en espacios euclidianos de cualquier dimensión.

A pesar del amplio uso de Descartes' enfoque, que se denominó geometría analítica, la definición del espacio euclidiano se mantuvo sin cambios hasta finales del siglo XIX. La introducción de espacios vectoriales abstractos permitió su uso en la definición de espacios euclidianos con una definición puramente algebraica. Se ha demostrado que esta nueva definición es equivalente a la definición clásica en términos de axiomas geométricos. Es esta definición algebraica la que ahora se usa más a menudo para introducir espacios euclidianos.

Motivación de la definición moderna

Una forma de pensar en el plano euclidiano es como un conjunto de puntos que satisfacen ciertas relaciones, expresables en términos de distancia y ángulos. Por ejemplo, hay dos operaciones fundamentales (referidas como movimientos) en el plano. Una es la traslación, que significa un desplazamiento del plano de modo que cada punto se desplaza en la misma dirección y la misma distancia. El otro es la rotación alrededor de un punto fijo en el plano, en el que todos los puntos en el plano giran alrededor de ese punto fijo en el mismo ángulo. Uno de los principios básicos de la geometría euclidiana es que dos figuras (generalmente consideradas como subconjuntos) del plano deben considerarse equivalentes (congruentes) si una puede transformarse en la otra mediante alguna secuencia de traslaciones, rotaciones y reflexiones (ver más abajo).

Para que todo esto sea matemáticamente preciso, la teoría debe definir claramente qué es un espacio euclidiano y las nociones relacionadas de distancia, ángulo, traslación y rotación. Incluso cuando se usa en teorías físicas, el espacio euclidiano es una abstracción separada de ubicaciones físicas reales, marcos de referencia específicos, instrumentos de medición, etc. Una definición puramente matemática del espacio euclidiano también ignora cuestiones de unidades de longitud y otras dimensiones físicas: la distancia en un espacio "matemático" el espacio es un número, no algo expresado en pulgadas o metros.

La forma estándar de definir matemáticamente un espacio euclidiano, como se lleva a cabo en el resto de este artículo, es como un conjunto de puntos sobre los que actúa un espacio vectorial real, el espacio de traslaciones que es equipado con un producto interior. La acción de las traslaciones hace del espacio un espacio afín, y esto permite definir líneas, planos, subespacios, dimensión y paralelismo. El producto interior permite definir distancias y ángulos.

El set $mathbb {R} ^{n}$ de $n$ -tuples de números reales equipados con el producto de punto es un espacio euclidiano de dimensión $n$ . Por el contrario, la elección de un punto llamado el origen y una base ortonormal del espacio de las traducciones es equivalente a definir un isomorfismo entre un espacio euclidiano de dimensión $n$ y $mathbb {R} ^{n}$ visto como un espacio euclidiano.

Sigue que todo lo que se puede decir sobre un espacio euclidiano también se puede decir sobre $mathbb{R} ^{n}.$ Por lo tanto, muchos autores, especialmente a nivel elemental, llaman $mathbb {R} ^{n}$ el espacio estándar Euclidean de la dimensión $n$ , o simplemente el Espacio euclidiano de dimensión $n$ .

Una razón para introducir una definición tan abstracta de los espacios euclidianos, y para trabajar con ella en lugar de $mathbb {R} ^{n}$ es que a menudo es preferible trabajar en un libres de coordenadas y sin origen (es decir, sin elegir una base preferida y un origen preferido). Otra razón es que no hay origen ni ninguna base en el mundo físico.

Definición técnica

A Espacio vectorial euclidiano es un espacio de producto interno de dimensión finita sobre los números reales.

Un espacio euclidiano es un espacio afín sobre los reales tal que el espacio vectorial asociado es un espacio vectorial euclidiano. Los espacios euclidianos a veces se denominan espacios afines euclidianos para distinguirlos de los espacios vectoriales euclidianos.

Si $E$ es un espacio euclidiano, su espacio vectorial asociado (espacio vectorial euclidiano) es a menudo denotado ${displaystyle {overrightarrow {E}}.}$ El dimensión de un espacio euclidiano es la dimensión de su espacio vectorial asociado.

Los elementos de $E$ se llaman puntos y son comúnmente denotados por letras mayúsculas. Los elementos de ${displaystyle {overrightarrow {E}}}$ se llaman vectores euroclidianos o vectores libres. También se llaman traducciones, aunque, correctamente hablando, una traducción es la transformación geométrica resultante de la acción de un vector Euclideano en el espacio Euclideano.

La acción de una traslación $v$ sobre un punto $P$ proporciona un punto que se denota $P + v$ . Esta acción satisface

{displaystyle P+(v+w)=(P+v)+w.}

Nota: El segundo $+$ en el lado izquierdo es una suma vectorial; todos los demás $+$ denotan una acción de un vector en un punto. Esta notación no es ambigua, ya que, para distinguir entre los dos significados de $+$ , basta mirar la naturaleza de su argumento izquierdo.

El hecho de que la acción sea libre y transitiva significa que por cada par de puntos $() P, Q)$ hay exactamente un vector de desplazamiento $v$ tales que $P + v = Q$ . Este vector $v$ es denotado $Q - P$ o ${displaystyle {overrightarrow {PQ}}.}$

Como se explicó anteriormente, algunas de las propiedades básicas de los espacios euclidianos resultan de la estructura del espacio afín. Se describen en § Estructura afín y sus subsecciones. Las propiedades resultantes del producto interior se explican en el § Estructura métrica y sus subapartados.

Ejemplos prototípicos

Para cualquier espacio vectorial, la suma actúa libre y transitivamente sobre el propio espacio vectorial. Por lo tanto, un espacio vectorial euclidiano puede verse como un espacio euclidiano que se tiene a sí mismo como espacio vectorial asociado.

Un caso típico del espacio vectorial Euclidean es $mathbb {R} ^{n}$ visto como un espacio vectorial equipado con el producto del punto como un producto interior. La importancia de este ejemplo particular del espacio euclidiano radica en el hecho de que cada espacio euclidiano es isomorfo para él. Más precisamente, dado un espacio euclidiano $E$ de la dimensión $n$ , la elección de un punto, llamado origen y una base ortonormal de ${displaystyle {overrightarrow {E}}}$ define un isomorfismo de los espacios euclidianos desde $E$ a $mathbb{R} ^{n}.$

Como cada espacio euclidiano de dimensión $n$ es isomorfo para él, el espacio euclidiano $mathbb {R} ^{n}$ a veces se llama espacio estándar Euclidean de la dimensión $n$ .

Estructura de espacio afín

Algunas propiedades básicas de los espacios euclidianos dependen únicamente del hecho de que un espacio euclidiano es un espacio afín. Se denominan propiedades afines e incluyen los conceptos de líneas, subespacios y paralelismo, que se detallan en las siguientes subsecciones.

Subespacios

Vamos $E$ ser un espacio euclidiano y ${displaystyle {overrightarrow {E}}}$ su espacio vectorial asociado.

Un plano, subespacio euclidiano o subespacio afín de $E$ es un subconjunto $F$ de $E$ tal que

{displaystyle {overrightarrow {F}}=left{{overrightarrow {PQ}}mid Pin F,Qin Fright}}

como el espacio vectorial asociado $F$ es un subespacial lineal (subespacial del vencedor) ${displaystyle {overrightarrow {E}}.}$ A Euclidean subspace $F$ es un espacio euclidiano con $overrightarrow F$ como el espacio vectorial asociado. Este subespacio lineal $overrightarrow F$ también se llama dirección de $F$ .

Si $P$ es un punto de $F$ entonces

{displaystyle F=left{P+vmid vin {overrightarrow {F}}right}.}

Por el contrario, si $P$ es un punto $E$ y ${displaystyle {overrightarrow {V}}}$ es un subespacio lineal ${displaystyle {overrightarrow {E}},}$ entonces

{displaystyle P+V=left{P+vmid vin Vright}}

es un subespacio Euclideano de dirección ${displaystyle {overrightarrow {V}}}$ . (El espacio vectorial asociado de este subespacio es ${displaystyle {overrightarrow {V}}}$ .)

Un espacio vectorial de Euclidean ${displaystyle {overrightarrow {E}}}$ (es decir, un espacio euclidiano que es igual a ${displaystyle {overrightarrow {E}}}$ ) tiene dos tipos de subespacios: sus subespacios euclidianos y sus subespacios lineales. Los subespacios lineales son subespaciales euclidianos y un subespacial euclidiano es un subespacial lineal si y sólo si contiene el vector cero.

Líneas y segmentos

En un espacio euclidiano, una línea es un subespacio euclidiano de dimensión uno. Dado que un espacio vectorial de dimensión uno es generado por cualquier vector distinto de cero, una línea es un conjunto de la forma

{displaystyle left{P+lambda {overrightarrow {PQ}}mid lambda in mathbb {R} right},}

donde $P$ y $Q$ son dos puntos distintos del espacio euclidiano como parte de la línea.

Se deduce que hay exactamente una recta que pasa por (contiene) dos puntos distintos. Esto implica que dos rectas distintas se cruzan como máximo en un punto.

Una representación más simétrica de la línea que pasa por $P$ y $Q$ es

{displaystyle left{O+(1-lambda){overrightarrow {OP}}+lambda {overrightarrow {OQ}}mid lambda in mathbb {R} right},}

donde $O$ es un punto arbitrario (no es necesario en la línea).

En un espacio vectorial euclidiano, el vector cero generalmente se elige para $O$ ; esto permite simplificar la fórmula anterior en

{displaystyle left{(1-lambda)P+lambda Qmid lambda in mathbb {R} right}.}

Una convención estándar permite usar esta fórmula en cada espacio euclidiano, consulte Espacio afín § Combinaciones afines y baricentro.

El segmento de línea, o simplemente segmento, que une los puntos $P$ y $Q$ es el subconjunto de puntos tales que $0 \leq 𝜆 \leq 1$ en las fórmulas anteriores. Se denota $PQ$ o $QP; es decir$

{displaystyle PQ=QP=left{P+lambda {overrightarrow {PQ}}mid 0leq lambda leq 1right}.}

Paralelismo

Dos subespacios $S$ y $T$ de la misma dimensión en un espacio euclidiano son paralelos si tienen la misma dirección (es decir, el mismo espacio vectorial asociado). De manera equivalente, son paralelos, si hay un vector de traducción $v$ que asigna uno al otro:

{displaystyle T=S+v.}

Dado un punto $P$ y un subespacio $S$ , existe exactamente un subespacio que contiene $P$ y es paralelo a $S$ , que es ${displaystyle P+{overrightarrow {S}}.}$ En el caso en que $S$ es una línea (subespacial de la dimensión uno), esta propiedad es el axioma de Playfair.

Se sigue que en un plano euclidiano, dos líneas se encuentran en un punto o son paralelas.

El concepto de subespacios paralelos se ha extendido a subespacios de diferentes dimensiones: dos subespacios son paralelos si la dirección de uno de ellos está contenida en la dirección del otro.

Estructura de espacio métrico

El espacio vectorial ${displaystyle {overrightarrow {E}}}$ asociado a un espacio euclidiano $E$ es un espacio interior de producto. Esto implica una forma bilineal simétrica

{displaystyle {begin{aligned}{overrightarrow {E}}times {overrightarrow {E}}&to mathbb {R} \(x,y)&mapsto langle x,yrangle end{aligned}}}

que es positivo definido (eso es $langle x,xrangle$ es siempre positivo $x ل 0$ ).

El producto interior de un espacio euclidiano se llama a menudo producto y denotado $x \cdot Sí.$ . Esto es especialmente el caso cuando se ha elegido un sistema de coordenadas cartesianas, ya que, en este caso, el producto interior de dos vectores es el producto de puntos de sus vectores de coordenadas. Por esta razón, y por razones históricas, la notación de puntos es más comúnmente utilizada que la notación de soporte para el producto interno de los espacios euclidianos. Este artículo seguirá este uso; es decir $langle x,yrangle$ será denotado $x \cdot Sí.$ en el resto de este artículo.

La norma euclidiana de un vector $x$ es

{displaystyle |x|={sqrt {xcdot x}}.}

El producto interno y la norma permiten expresar y probar propiedades métricas y topológicas de la geometría euclidiana. La siguiente subsección describe los más fundamentales. En estas subsecciones, $E$ denota un espacio euclidiano arbitrario, y ${displaystyle {overrightarrow {E}}}$ denota su espacio vectorial de traducciones.

Distancia y longitud

La distancia (más precisamente, la distancia euclidiana) entre dos puntos de un espacio euclidiano es la norma del vector de traslación que relaciona un punto con el otro; es decir

{displaystyle d(P,Q)={Bigl |}{overrightarrow {PQ}}{vphantom {frac {|}{}}}{Bigr |}.}

El longitud de un segmento $PQ$ es la distancia $d () P, Q)$ entre sus puntos finales P y Q. A menudo se denota ${displaystyle |PQ|}$ .

La distancia es una métrica, ya que es definida positiva, simétrica y satisface la desigualdad del triángulo

{displaystyle d(P,Q)leq d(P,R)+d(R,Q).}

Además, la igualdad es verdadera si y solo si un punto $R$ pertenece al segmento <span class="texhtml" PQ. Esta desigualdad significa que la longitud de cualquier arista de un triángulo es menor que la suma de las longitudes de las otras aristas. Este es el origen del término desigualdad triangular.

Con la distancia euclidiana, todo espacio euclidiano es un espacio métrico completo.

Ortogonalidad

Dos vectores no cero $u$ y $v$ de ${displaystyle {overrightarrow {E}}}$ (el espacio vectorial asociado de un espacio euclidiano $E$ ) perpendicular o ortogonal si su producto interno es cero:

{displaystyle ucdot v=0}

Dos subespacios lineales de ${displaystyle {overrightarrow {E}}}$ son ortogonales si cada vector no cero del primero es perpendicular a cada vector no cero del segundo. Esto implica que la intersección de los subespacios lineales se reduce al vector cero.

Dos líneas y, más generalmente, dos subespacios euclidianos (una línea puede considerarse como un subespacio euclidiano) son ortogonales si sus direcciones (los espacios vectoriales asociados de los subespacios euclidianos) son ortogonales. Dos rectas ortogonales que se cortan se dicen perpendiculares.

Dos segmentos $AB$ y $AC$ que comparten un punto final común $A$ son perpendicular o forma un ángulo recto si los vectores ${displaystyle {overrightarrow {AB}}}$ y ${displaystyle {overrightarrow {AC}}}$ son ortogonales.

Si $AB$ y $AC$ forman un ángulo recto, uno tiene

{displaystyle |BC|^{2}=|AB|^{2}+|AC|^{2}.}

Este es el teorema de Pitágoras. Su demostración es fácil en este contexto, ya que, expresándolo en términos del producto interno, se tiene, usando la bilinealidad y la simetría del producto interno:

{displaystyle {begin{aligned}|BC|^{2}&={overrightarrow {BC}}cdot {overrightarrow {BC}}\&=left({overrightarrow {BA}}+{overrightarrow {AC}}right)cdot left({overrightarrow {BA}}+{overrightarrow {AC}}right)\&={overrightarrow {BA}}cdot {overrightarrow {BA}}+{overrightarrow {AC}}cdot {overrightarrow {AC}}-2{overrightarrow {AB}}cdot {overrightarrow {AC}}\&={overrightarrow {AB}}cdot {overrightarrow {AB}}+{overrightarrow {AC}}cdot {overrightarrow {AC}}\&=|AB|^{2}+|AC|^{2}.end{aligned}}}

Aquí, ${displaystyle {overrightarrow {AB}}cdot {overrightarrow {AC}}=0}$ se utiliza ya que estos dos vectores son ortogonales.

Ángulo

Ángulos positivos y negativos en el plano orientado

El (no orientado) ángulo $Silencio$ entre dos vectores no cero $x$ y $Sí.$ dentro ${displaystyle {overrightarrow {E}}}$ es

{displaystyle theta =arccos left({frac {xcdot y}{left|xright|left|yright|}}right)}

donde $arccos$ es el valor principal de la función arcocoseno. Por la desigualdad de Cauchy-Schwarz, el argumento del arcocoseno está en el intervalo $[-1, 1]$ . Por lo tanto $θ$ es real, y $0 \leq θ \leq π$ (o $0 \leq θ \leq 180$ si los ángulos se miden en grados).

Los ángulos no son útiles en una línea euclidiana, ya que solo pueden ser 0 o $π$ .

En un plano euclidiano orientado, se puede definir el ángulo orientado de dos vectores. El ángulo orientado de dos vectores $x$ y $y$ es entonces el opuesto del ángulo orientado de $y$ y $x$ . En este caso, el ángulo de dos vectores puede tener cualquier valor módulo un múltiplo entero de $2 π$ . En particular, un ángulo reflejo $π < θ < 2 π$ es igual al ángulo negativo $- π < θ - 2 π < 0$ .

El ángulo de dos vectores no cambia si se multiplican por números positivos. Más precisamente, si $x$ y $y$ son dos vectores, y $λ$ y $μ$ son números reales, entonces

{displaystyle operatorname {angle} (lambda x,mu y)={begin{cases}operatorname {angle} (x,y)qquad qquad {text{if }}lambda {text{ and }}mu {text{ have the same sign}}\pi -operatorname {angle} (x,y)qquad {text{otherwise}}.end{cases}}}

Si $A$ , $B$ , y $C$ son tres puntos en un espacio euclidiano, el ángulo de los segmentos $AB$ y $AC$ es el ángulo de los vectores ${displaystyle {overrightarrow {AB}}}$ y ${displaystyle {overrightarrow {AC}}.}$ Como la multiplicación de vectores por números positivos no cambia el ángulo, el ángulo de dos líneas medias con punto inicial $A$ se puede definir: es el ángulo de los segmentos $AB$ y $AC$ , donde $B$ y $C$ son puntos arbitrarios, uno en cada línea media. Aunque esto es menos utilizado, se puede definir de forma similar el ángulo de segmentos o líneas medias que no comparten un punto inicial.

El ángulo de dos líneas se define de la siguiente manera. Si $θ$ es el ángulo de dos segmentos, uno en cada línea, el ángulo de otros dos segmentos cualesquiera, uno en cada línea, es $θ$ o $π - θ$ . Uno de estos ángulos está en el intervalo $[0, π /2]$ , y el otro está en $[π /2, π]$ . El ángulo no orientado de las dos líneas es el del intervalo $[0, π /2]$ . En un plano euclidiano orientado, el ángulo orientado de dos rectas pertenece al intervalo $[- π /2, π /2]$ .

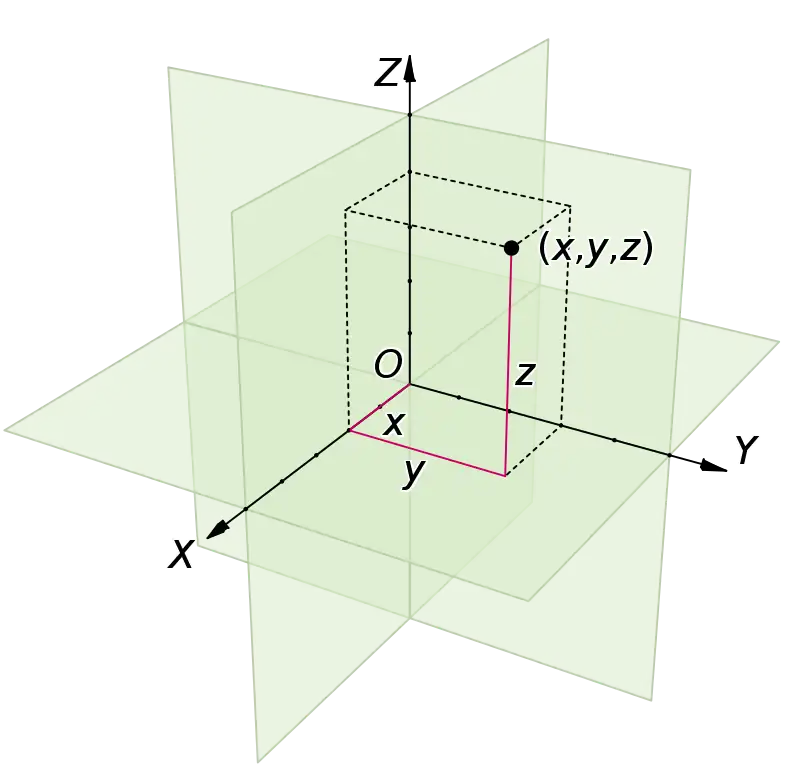
Coordenadas cartesianas

Cada espacio vectorial Euclideano tiene una base ortonormal (de hecho, infinitamente muchos en dimensión superior a uno, y dos en dimensión uno), esa es una base ${displaystyle (e_{1},dotse_{n})}$ de vectores de unidad ( ${displaystyle |e_{i}|=1}$ ) que son dos veces ortogonal ( ${displaystyle e_{i}cdot e_{j}=0}$ para $i ل j$ ). Más precisamente, dada cualquier base ${displaystyle (b_{1},dotsb_{n}),}$ el proceso Gram-Schmidt calcula una base ortonormal tal que, por cada $i$ , los lados lineales de ${displaystyle (e_{1},dotse_{i})}$ y ${displaystyle (b_{1},dotsb_{i})}$ son iguales.

Dado un espacio euclidiano $E$ , a Marco cartesiano es un conjunto de datos consistentes en una base ortonormal de ${displaystyle {overrightarrow {E}},}$ y un punto $E$ , llamado el origen y a menudo denotado $O$ . Un marco cartesiano ${displaystyle (O,e_{1},dotse_{n})}$ permite definir coordenadas cartesianas para ambos $E$ y ${displaystyle {overrightarrow {E}}}$ de la siguiente manera.

Las coordenadas cartesianas de un vector $v$ de ${displaystyle {overrightarrow {E}}}$ son los coeficientes de $v$ sobre la base ortonormal ${displaystyle e_{1},dotse_{n}.}$ Por ejemplo, las coordenadas cartesianas de un vector $v$ sobre una base ortonormal ${displaystyle (e_{1},e_{2},e_{3})}$ (que puede ser nombrado como $(x,y,z)$ como convención) en un espacio Euclideano tridimensional es ${displaystyle (alpha _{1},alpha _{2},alpha _{3})}$ si ${displaystyle v=alpha _{1}e_{1}+alpha _{2}e_{2}+alpha _{3}e_{3}}$ . Como la base es ortonormal, la $i$ - Coeficiente $alpha _{i}$ es igual al producto de puntos ${displaystyle vcdot e_{i}.}$

Las coordenadas cartesianas de un punto $P$ de $E$ son las coordenadas cartesianas del vector ${displaystyle {overrightarrow {OP}}.}$

Otras coordenadas

Coordenadas tridimensionales

Como un espacio euclidiano es un espacio afín, se puede considerar un marco afín en él, que es lo mismo que un marco euclidiano, excepto que no se requiere que la base sea ortonormal. Esto define coordenadas afines, a veces llamadas coordenadas sesgadas para enfatizar que los vectores base no son ortogonales por pares.

Una base afín de un espacio euclidiano de dimensión $n$ es un conjunto de $n + 1$ puntos que no están contenidos en un hiperplano. Una base afín define coordenadas baricéntricas para cada punto.

Muchos otros sistemas de coordenadas se pueden definir en un espacio euclidiano $E$ de la dimensión $n$ , de la siguiente manera. Vamos $f$ ser un homeomorfismo (o, más a menudo, un diffeomorfismo) de un subconjunto abierto denso $E$ a un subconjunto abierto $mathbb{R} ^{n}.$ El coordenadas de un punto $x$ de $E$ son los componentes $f () x)$ . El sistema de coordenadas polares (dimensión 2) y los sistemas de coordinación esférica y cilíndrica (dimensión 3) se definen de esta manera.

Para los puntos que están fuera del dominio de $f$ , las coordenadas a veces se pueden definir como el límite de las coordenadas de los puntos vecinos, pero estas coordenadas pueden no estar definidas unívocamente y pueden no ser continuas en la vecindad del punto. Por ejemplo, para el sistema de coordenadas esféricas, la longitud no está definida en el polo, y en el antimeridiano, la longitud pasa discontinuamente de –180° a +180°.

Esta forma de definir coordenadas se extiende fácilmente a otras estructuras matemáticas y, en particular, a las variedades.

Isometrías

Una isometría entre dos espacios métricos es una biyección que conserva la distancia, es decir

{displaystyle d(f(x),f(y))=d(x,y).}

En el caso de un espacio vectorial euclidiano, una isometría que asigna el origen al origen conserva la norma

{displaystyle |f(x)|=|x|,}

ya que la norma de un vector es su distancia desde el vector cero. Conserva también el producto interior.

{displaystyle f(x)cdot f(y)=xcdot y,}

desde

{displaystyle xcdot y={frac {1}{2}}left(|x+y|^{2}-|x|^{2}-|y|^{2}right).}

Una isometría de espacios vectoriales euclidianos es un isomorfismo lineal.

Una isometría ${displaystyle fcolon Eto F}$ de los espacios euclidianos define una isometría ${displaystyle {overrightarrow {f}}colon {overrightarrow {E}}to {overrightarrow {F}}}$ de los espacios vectoriales Euclidesanos asociados. Esto implica que dos espacios euroclidianos isométricos tienen la misma dimensión. Por el contrario, si $E$ y $F$ son espacios euclidianos, $O ▪ E$ , $O . ▪ F$ , y ${displaystyle {overrightarrow {f}}colon {overrightarrow {E}}to {overrightarrow {F}}}$ es una isometría, luego el mapa ${displaystyle fcolon Eto F}$ definidas por

{displaystyle f(P)=O'+{overrightarrow {f}}left({overrightarrow {OP}}right)}

es una isometría de espacios euclidianos.

De los resultados anteriores se deduce que una isometría de espacios euclidianos asigna líneas a líneas y, más generalmente, subespacios euclidianos a subespacios euclidianos de la misma dimensión, y que la restricción de la isometría en estos subespacios son isometrías de estos subespacios.

Isometría con ejemplos prototípicos

Si $E$ es un espacio euclidiano, su espacio vectorial asociado ${displaystyle {overrightarrow {E}}}$ puede considerarse como un espacio euclidiano. Cada punto $O ▪ E$ define una isometría de espacios euclidianos

{displaystyle Pmapsto {overrightarrow {OP}},}

que asigna $O$ al vector cero y tiene la identidad como mapa lineal asociado. La isometría inversa es el mapa.

{displaystyle vmapsto O+v.}

Un marco euclidiano ${displaystyle (O,e_{1},dotse_{n})}$ permite definir el mapa

{displaystyle {begin{aligned}E&to mathbb {R} ^{n}\P&mapsto left(e_{1}cdot {overrightarrow {OP}},dotse_{n}cdot {overrightarrow {OP}}right),end{aligned}}}

que es una isometría de espacios euclidianos. La isometría inversa es

{displaystyle {begin{aligned}mathbb {R} ^{n}&to E\(x_{1}dotsx_{n})&mapsto left(O+x_{1}e_{1}+dots +x_{n}e_{n}right).end{aligned}}}

Esto significa que, salvo un isomorfismo, existe exactamente un espacio euclidiano de una dimensión dada.

Esto justifica que muchos autores hablen de $mathbb {R} ^{n}$ como el Espacio euclidiano de dimensión $n$ .

Grupo euclidiano

Una isometría de un espacio euclidiano sobre sí mismo se denomina isometría euclidiana, transformación euclidiana o transformación rígida. Las transformaciones rígidas de un espacio euclidiano forman un grupo (bajo composición), llamado grupo euclidiano y a menudo denotado $E(n)$ de $ISO(n)$ .

Las transformaciones euclidianas más simples son las traslaciones

{displaystyle Pto P+v.}

Están en correspondencia biyectiva con vectores. Esta es una razón para llamar espacio de traslaciones al espacio vectorial asociado a un espacio euclidiano. Las traslaciones forman un subgrupo normal del grupo euclidiano.

Una isometría euclidiana $f$ de un espacio euclidiano $E$ define una isometría lineal ${displaystyle {overrightarrow {f}}}$ del espacio vectorial asociado (por isometría lineal, se refiere a una isometría que también es un mapa lineal) de la siguiente manera: $Q - P$ el vector ${displaystyle {overrightarrow {PQ}}}$ , si $O$ es un punto arbitrario $E$ , uno tiene

{displaystyle {overrightarrow {f}}({overrightarrow {OP}})=f(P)-f(O).}

Es sencillo probar que este es un mapa lineal que no depende de la elección de $O.$

El mapa ${displaystyle fto {overrightarrow {f}}}$ es un grupo homomorfismo del grupo Euclideano sobre el grupo de isometrías lineales, llamado grupo ortogonal. El núcleo de este homomorfismo es el grupo de traducción, mostrando que es un subgrupo normal del grupo Euclideano.

Las isometrías que fijan un punto dado $P$ forman el subgrupo estabilizador del grupo euclidiano con respecto a $P$ . La restricción a este estabilizador del homomorfismo del grupo anterior es un isomorfismo. Entonces las isometrías que fijan un punto dado forman un grupo isomorfo al grupo ortogonal.

Vamos $P$ ser un punto, $f$ una isometría, y $t$ la traducción que mapas $P$ a $f () P)$ . La isometría ${displaystyle g=t^{-1}circ f}$ soluciones $P$ . Así que... ${displaystyle f=tcirc g,}$ y el grupo Euclidean es el producto semidirecto del grupo de traducción y el grupo ortogonal.

El grupo ortogonal especial es el subgrupo normal del grupo ortogonal que conserva la entrega. Es un subgrupo del índice dos del grupo ortogonal. Su imagen inversa por el homomorfismo grupo ${displaystyle fto {overrightarrow {f}}}$ es un subgrupo normal del índice dos del grupo Euclideano, que se llama el grupo especial Euclidean o el grupo de desplazamiento. Sus elementos se llaman movimientos rígidos o desplazamientos.

Los movimientos rígidos incluyen la identidad, las traslaciones, las rotaciones (los movimientos rígidos que fijan al menos un punto) y también los movimientos de tornillo.

Los ejemplos típicos de transformaciones rígidas que no son movimientos rígidos son los reflejos, que son transformaciones rígidas que fijan un hiperplano y no son la identidad. Son también las transformaciones consistentes en cambiar el signo de una coordenada sobre algún marco euclidiano.

Como el grupo euclidiano especial es un subgrupo del índice dos del grupo euclidiano, dada una reflexión $r$ , toda transformación rígida que no es un movimiento rígido es el producto de $r$ y un movimiento rígido. Un reflejo de deslizamiento es un ejemplo de una transformación rígida que no es un movimiento rígido ni un reflejo.

Todos los grupos que se han considerado en esta sección son grupos de Lie y grupos algebraicos.

Topología

La distancia euclidiana hace que un espacio euclidiano sea un espacio métrico, y por lo tanto un espacio topológico. Esta topología se llama la topología Euclideana. En el caso de $mathbb {R} ^{n},$ esta topología es también la topología del producto.

Los conjuntos abiertos son los subconjuntos que contienen una bola abierta alrededor de cada uno de sus puntos. En otras palabras, las bolas abiertas forman la base de la topología.

La dimensión topológica de un espacio euclidiano es igual a su dimensión. Esto implica que los espacios euclidianos de diferentes dimensiones no son homeomorfos. Además, el teorema de invariancia del dominio afirma que un subconjunto de un espacio euclidiano es abierto (para la topología del subespacio) si y solo si es homeomorfo a un subconjunto abierto de un espacio euclidiano de la misma dimensión.

Los espacios euclidianos son completos y localmente compactos. Es decir, un subconjunto cerrado de un espacio euclidiano es compacto si está acotado (es decir, contenido en una bola). En particular, las bolas cerradas son compactas.

Definiciones axiomáticas

La definición de espacios euclidianos que se ha descrito en este artículo difiere fundamentalmente de la de Euclides. En realidad, Euclides no definió formalmente el espacio, pues se pensó como una descripción del mundo físico que existe independientemente de la mente humana. La necesidad de una definición formal apareció solo a fines del siglo XIX, con la introducción de geometrías no euclidianas.

Se han utilizado dos enfoques diferentes. Felix Klein sugirió definir geometrías a través de sus simetrías. La presentación de los espacios euclidianos que se da en este artículo proviene esencialmente de su programa de Erlangen, con énfasis en los grupos de traslaciones e isometrías.

Por otro lado, David Hilbert propuso un conjunto de axiomas, inspirado en los postulados de Euclides. Pertenecen a la geometría sintética, ya que no implican ninguna definición de números reales. Más tarde, G. D. Birkhoff y Alfred Tarski propusieron conjuntos de axiomas más simples, que utilizan números reales (véanse los axiomas de Birkhoff y los axiomas de Tarski).

En Álgebra geométrica, Emil Artin ha demostrado que todas estas definiciones de un espacio euclidiano son equivalentes. Es bastante fácil demostrar que todas las definiciones de los espacios euclidianos satisfacen los axiomas de Hilbert y que las que involucran números reales (incluida la definición anterior) son equivalentes. La parte difícil de la demostración de Artin es la siguiente. En los axiomas de Hilbert, la congruencia es una relación de equivalencia sobre segmentos. Uno puede así definir la longitud de un segmento como su clase de equivalencia. Por lo tanto, se debe probar que esta longitud satisface las propiedades que caracterizan a los números reales no negativos. Artin demostró esto con axiomas equivalentes a los de Hilbert.

Uso

Desde los antiguos griegos, el espacio euclidiano se usa para modelar formas en el mundo físico. Por lo tanto, se utiliza en muchas ciencias, como la física, la mecánica y la astronomía. También es muy utilizado en todas las áreas técnicas que se ocupan de las formas, la figura, la ubicación y la posición, como la arquitectura, la geodesia, la topografía, la navegación, el diseño industrial o el dibujo técnico.

El espacio de dimensiones superiores a tres aparece en varias teorías modernas de la física; ver Dimensión superior. Ocurren también en espacios de configuración de sistemas físicos.

Además de la geometría euclidiana, los espacios euclidianos también se utilizan ampliamente en otras áreas de las matemáticas. Los espacios tangentes de variedades diferenciables son espacios vectoriales euclidianos. De manera más general, una variedad es un espacio que se aproxima localmente mediante espacios euclidianos. La mayoría de las geometrías no euclidianas pueden modelarse mediante una variedad e incrustarse en un espacio euclidiano de mayor dimensión. Por ejemplo, un espacio elíptico puede ser modelado por un elipsoide. Es común representar en un espacio euclidiano objetos matemáticos que a priori no son de naturaleza geométrica. Un ejemplo entre muchos es la representación habitual de grafos.

Otros espacios geométricos

Desde la introducción, a fines del siglo XIX, de las geometrías no euclidianas, se han considerado muchos tipos de espacios, sobre los cuales se puede hacer un razonamiento geométrico de la misma manera que con los espacios euclidianos. En general, comparten algunas propiedades con los espacios euclidianos, pero también pueden tener propiedades que pueden parecer bastante extrañas. Algunos de estos espacios utilizan geometría euclidiana para su definición, o pueden modelarse como subespacios de un espacio euclidiano de mayor dimensión. Cuando dicho espacio está definido por axiomas geométricos, incrustar el espacio en un espacio euclidiano es una forma estándar de probar la consistencia de su definición o, más precisamente, de probar que su teoría es consistente, si la geometría euclidiana es consistente (lo que no puede probarse).).

Espacio afín

Un espacio euclidiano es un espacio afín equipado con una métrica. Los espacios afines tienen muchos otros usos en matemáticas. En particular, al estar definidos sobre cualquier campo, permiten hacer geometría en otros contextos.

Tan pronto como se consideran preguntas no lineales, generalmente es útil considerar espacios afines sobre los números complejos como una extensión de los espacios euclidianos. Por ejemplo, un círculo y una línea siempre tienen dos puntos de intersección (posiblemente no distintos) en el espacio afín complejo. Por lo tanto, la mayor parte de la geometría algebraica se construye en espacios afines complejos y espacios afines sobre campos algebraicamente cerrados. Las formas que se estudian en geometría algebraica en estos espacios afines se denominan variedades algebraicas afines.

Los espacios afines sobre los números racionales y, de manera más general, sobre los campos numéricos algebraicos proporcionan un vínculo entre la geometría (algebraica) y la teoría de números. Por ejemplo, el último teorema de Fermat puede afirmarse: 'una curva de Fermat de grado superior a dos no tiene punto en el plano afín sobre los racionales'.

La geometría en espacios afines sobre campos finitos también ha sido ampliamente estudiada. Por ejemplo, las curvas elípticas sobre campos finitos se utilizan ampliamente en criptografía.

Espacio proyectivo

Originalmente, los espacios proyectivos se introdujeron agregando "puntos en el infinito" a espacios euclidianos y, más generalmente, a espacios afines, para hacer verdadera la afirmación "dos líneas coplanares se encuentran exactamente en un punto". Los espacios proyectivos comparten con los espacios euclidianos y afines la propiedad de ser isótropos, es decir, no existe una propiedad del espacio que permita distinguir entre dos puntos o dos líneas. Por tanto, se suele utilizar una definición más isotrópica, que consiste en definir un espacio proyectivo como el conjunto de las líneas vectoriales en un espacio vectorial de dimensión uno más.

En cuanto a los espacios afines, los espacios proyectivos se definen sobre cualquier campo, y son espacios fundamentales de la geometría algebraica.

Geometrías no euclidianas

La geometría no euclidiana se refiere generalmente a espacios geométricos donde el postulado de las paralelas es falso. Incluyen la geometría elíptica, donde la suma de los ángulos de un triángulo es mayor a 180°, y la geometría hiperbólica, donde esta suma es menor a 180°. Su introducción en la segunda mitad del siglo XIX, y la prueba de que su teoría es consistente (si la geometría euclidiana no es contradictoria) es una de las paradojas que están en el origen de la crisis fundacional de las matemáticas de principios del siglo XX, y motivó la sistematización de teorías axiomáticas en matemáticas.

Espacios curvos

Una variedad es un espacio que en la vecindad de cada punto se parece a un espacio euclidiano. En términos técnicos, una variedad es un espacio topológico, tal que cada punto tiene una vecindad que es homeomorfa a un subconjunto abierto de un espacio euclidiano. Las variedades se pueden clasificar según el grado creciente de esta "semejanza" en variedades topológicas, variedades diferenciables, variedades suaves y variedades analíticas. Sin embargo, ninguno de estos tipos de "parecidos" respetar distancias y ángulos, incluso aproximadamente.

Las distancias y los ángulos se pueden definir en una variedad suave al proporcionar una métrica euclidiana que varía suavemente en los espacios tangentes en los puntos de la variedad (estos espacios tangentes son, por lo tanto, espacios vectoriales euclidianos). Esto da como resultado una variedad de Riemann. En general, las líneas rectas no existen en una variedad de Riemann, pero su papel lo desempeñan las geodésicas, que son los "caminos más cortos" entre dos puntos. Esto permite definir distancias, que se miden a lo largo de geodésicas, y ángulos entre geodésicas, que son el ángulo de sus tangentes en el espacio tangente en su intersección. Entonces, las variedades de Riemann se comportan localmente como un espacio euclidiano que ha sido doblado.

Los espacios euclidianos son variedades trivialmente riemannianas. Un ejemplo que ilustra este pozo es la superficie de una esfera. En este caso, las geodésicas son arcos de círculo máximo, que se denominan ortodrómicas en el contexto de la navegación. De manera más general, los espacios de geometrías no euclidianas se pueden realizar como variedades de Riemann.

Espacio pseudo-euclidiano

Un producto interno de un espacio vectorial real es una forma bilineal definida positiva y, por lo tanto, caracterizada por una forma cuadrática definida positiva. Un espacio pseudo-euclidiano es un espacio afín con un espacio vectorial real asociado equipado con una forma cuadrática no degenerada (que puede ser indefinida).

Un ejemplo fundamental de dicho espacio es el espacio de Minkowski, que es el espacio-tiempo de la relatividad especial de Einstein. Es un espacio de cuatro dimensiones, donde la métrica está definida por la forma cuadrática

{displaystyle x^{2}+y^{2}+z^{2}-t^{2},}

donde la última coordenada (t) es temporal, y las otras tres (x, y, z) son espaciales.

Para tener en cuenta la gravedad, la relatividad general utiliza una variedad pseudo-riemanniana que tiene espacios de Minkowski como espacios tangentes. La curvatura de esta variedad en un punto es función del valor del campo gravitatorio en ese punto.

Contenido relacionado

Más resultados...