Tendencia central (estadística)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En estadística, una tendencia central (o medida de tendencia central ) es un valor central o típico para una distribución de probabilidad. También puede denominarse centro o ubicación de la distribución. Coloquialmente, las medidas de tendencia central a menudo se denominan promedios. El término tendencia central data de finales de la década de 1920.

Las medidas de tendencia central más comunes son la media aritmética, la mediana y la moda. Se puede calcular una tendencia media para un conjunto finito de valores o para una distribución teórica, como la distribución normal. Ocasionalmente, los autores usan la tendencia central para denotar "la tendencia de los datos cuantitativos a agruparse en torno a algún valor central".

La tendencia central de una distribución se suele contrastar con su dispersión o variabilidad ; la dispersión y la tendencia central son las propiedades a menudo caracterizadas de las distribuciones. El análisis puede juzgar si los datos tienen una tendencia central fuerte o débil en función de su dispersión.

Medidas

Determinación de las tendencias centrales de una población estadística

Lo siguiente puede aplicarse a datos unidimensionales. Dependiendo de las circunstancias, puede ser apropiado transformar los datos antes de calcular una tendencia central. Los ejemplos son elevar al cuadrado los valores o tomar logaritmos. Si una transformación es apropiada y lo que debería ser, depende en gran medida de los datos que se analizan.Media aritmética o simplemente mediala suma de todas las mediciones dividida por el número de observaciones en el conjunto de datos.Medianael valor medio que separa la mitad superior de la mitad inferior del conjunto de datos. La mediana y la moda son las únicas medidas de tendencia central que se pueden usar para datos ordinales, en los que los valores se clasifican entre sí pero no se miden de forma absoluta.Modoel valor más frecuente en el conjunto de datos. Esta es la única medida de tendencia central que se puede utilizar con datos nominales, que tienen asignaciones de categorías puramente cualitativas.Significado geometricola raíz enésima del producto de los valores de los datos, donde hay n de estos. Esta medida es válida solo para datos que se miden absolutamente en una escala estrictamente positiva.Significado armonicoel recíproco de la media aritmética de los recíprocos de los valores de los datos. Esta medida también es válida solo para datos que se miden absolutamente en una escala estrictamente positiva.media aritmética ponderadauna media aritmética que incorpora ponderación a ciertos elementos de datos.Media truncada o media recortadala media aritmética de los valores de datos después de descartar un cierto número o proporción de los valores de datos más altos y más bajos.Media intercuartiluna media truncada basada en datos dentro del rango intercuartílico.Rango mediola media aritmética de los valores máximo y mínimo de un conjunto de datos.Bisagra mediala media aritmética del primer y tercer cuartil.Trimeanla media aritmética ponderada de la mediana y dos cuartiles.Media Winsorizadauna media aritmética en la que los valores extremos se reemplazan por valores más cercanos a la mediana.

Cualquiera de los anteriores puede aplicarse a cada dimensión de datos multidimensionales, pero los resultados pueden no ser invariantes a las rotaciones del espacio multidimensional. Además, están losmediana geométricaque minimiza la suma de las distancias a los puntos de datos. Esto es lo mismo que la mediana cuando se aplica a datos unidimensionales, pero no es lo mismo que tomar la mediana de cada dimensión de forma independiente. No es invariante a diferentes reescalados de las diferentes dimensiones.Media cuadrática (a menudo conocida como la raíz cuadrada media)útil en ingeniería, pero no se usa a menudo en estadística. Esto se debe a que no es un buen indicador del centro de la distribución cuando la distribución incluye valores negativos.Profundidad simplela probabilidad de que un símplex elegido al azar con vértices de la distribución dada contenga el centro dadoMediana de Tukeyun punto con la propiedad de que cada semiespacio que lo contiene también contiene muchos puntos muestrales

Soluciones a problemas variacionales

Varias medidas de tendencia central se pueden caracterizar por resolver un problema variacional, en el sentido del cálculo de variaciones, es decir, minimizar la variación desde el centro. Es decir, dada una medida de dispersión estadística, se pide una medida de tendencia central que minimice la variación: tal que la variación desde el centro sea mínima entre todas las opciones de centro. En broma, "la dispersión precede a la ubicación". Estas medidas se definen inicialmente en una dimensión, pero se pueden generalizar a múltiples dimensiones. Este centro puede o no ser único. En el sentido de L espacios, la correspondencia es:

L	dispersión	tendencia central
`L`	relación de variación	modo
`L`	desviación absoluta media	mediana (mediana geométrica)
`L`	Desviación Estándar	media (centroide)
`L`	desviación máxima	rango medio

Las funciones asociadas se denominan p -normas: respectivamente 0-"norma", 1-norma, 2-norma y ∞-norma. La función correspondiente al espacio L no es una norma y, por lo tanto, a menudo se la menciona entre comillas: 0-"norma".

En ecuaciones, para un conjunto de datos dado (finito) X , considerado como un vector x = ( x ₁ ,…, x _n ) , la dispersión alrededor de un punto c es la "distancia" desde x hasta el vector constante c = ( c ,…, c ) en la norma p (normalizada por el número de puntos n ): $f_{p}(c)=\left\|\mathbf {x} -\mathbf {c} \right\|_{p}:={\bigg (}{\frac {1}{n} }\sum _{i=1}^{n}\left|x_{i}-c\right|^{p}{\bigg)}^{1/p}$

Para p = 0 y p = ∞ estas funciones se definen tomando límites, respectivamente, como p → 0 y p → ∞ . Para p = 0 , los valores límite son 0 = 0 y a = 0 o a ≠ 0 , por lo que la diferencia se convierte simplemente en igualdad, por lo que la norma 0 cuenta el número de puntos desiguales . Para p = ∞ domina el número más grande y, por lo tanto, la norma ∞ es la diferencia máxima.

Unicidad

La media ( centro L ) y el rango medio ( centro L ) son únicos (cuando existen), mientras que la mediana ( centro L ) y la moda ( centro L ) no son en general únicas. Esto puede entenderse en términos de convexidad de las funciones asociadas (funciones coercitivas).

La norma 2 y la norma ∞ son estrictamente convexas y, por lo tanto (por optimización convexa), el minimizador es único (si existe) y existe para distribuciones acotadas. Por lo tanto, la desviación estándar sobre la media es menor que la desviación estándar sobre cualquier otro punto, y la desviación máxima sobre el rango medio es menor que la desviación máxima sobre cualquier otro punto.

La norma 1 no es estrictamente convexa, mientras que se necesita una convexidad estricta para garantizar la unicidad del minimizador. En consecuencia, la mediana (en este sentido de minimización) no es en general única y, de hecho, cualquier punto entre los dos puntos centrales de una distribución discreta minimiza la desviación absoluta promedio.

El 0-"norma" no es convexo (por lo tanto, no es una norma). En consecuencia, la moda no es única; por ejemplo, en una distribución uniforme, cualquier punto es la moda.

Agrupación

En lugar de un solo punto central, se pueden solicitar múltiples puntos de modo que se minimice la variación de estos puntos. Esto conduce al análisis de conglomerados, donde cada punto del conjunto de datos se agrupa con el "centro" más cercano. Más comúnmente, el uso de la norma 2 generaliza la agrupación de media a k medias, mientras que el uso de la norma 1 generaliza la agrupación (geométrica) de mediana a k medianas. El uso de la norma 0 simplemente generaliza la moda (valor más común) para usar los k valores más comunes como centros.

A diferencia de las estadísticas de un solo centro, esta agrupación multicéntrica en general no puede calcularse en una expresión de forma cerrada y, en cambio, debe calcularse o aproximarse mediante un método iterativo; un enfoque general son los algoritmos de maximización de expectativas.

geometría de la información

La noción de un "centro" que minimiza la variación puede generalizarse en la geometría de la información como una distribución que minimiza la divergencia (una distancia generalizada) de un conjunto de datos. El caso más común es la estimación de máxima verosimilitud, donde la estimación de máxima verosimilitud (MLE) maximiza la probabilidad (minimiza la sorpresa esperada), que se puede interpretar geométricamente utilizando la entropía para medir la variación: la MLE minimiza la entropía cruzada (equivalentemente, entropía relativa, Kullback– divergencia de Leibler).

Un ejemplo simple de esto es para el centro de datos nominales: en lugar de usar la moda (el único "centro" de un solo valor), a menudo se usa la medida empírica (la distribución de frecuencias dividida por el tamaño de la muestra) como un "centro". . Por ejemplo, dados datos binarios, digamos cara o cruz, si un conjunto de datos consta de 2 caras y 1 cruz, entonces la moda es "cara", pero la medida empírica es 2/3 caras, 1/3 cruces, lo que minimiza el entropía cruzada (sorpresa total) del conjunto de datos. Esta perspectiva también se usa en el análisis de regresión, donde los mínimos cuadrados encuentran la solución que minimiza las distancias desde ella, y análogamente en la regresión logística, una estimación de máxima verosimilitud minimiza la sorpresa (distancia de información).

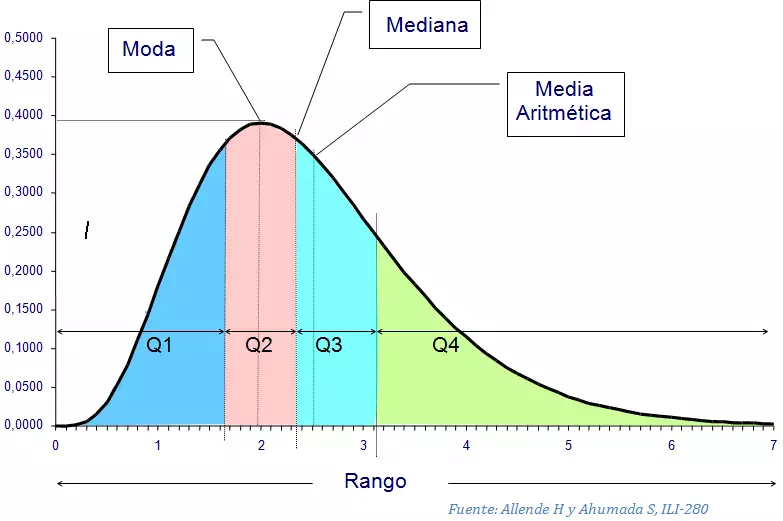
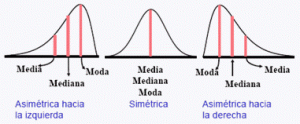
Relaciones entre la media, la mediana y la moda

Para distribuciones unimodales, los siguientes límites son conocidos y definidos: ${\frac {|\theta -\mu |}{\sigma}}\leq {\sqrt {3}},$ ${\frac {|\nu -\mu |}{\sigma}}\leq {\sqrt {0.6}},$ ${\frac {|\theta -\nu |}{\sigma}}\leq {\sqrt {3}},$

donde μ es la media, ν es la mediana, θ es la moda y σ es la desviación estándar.

Para cada distribución, ${\frac {|\nu -\mu |}{\sigma}}\leq 1.$

Contenido relacionado

Más resultados...