Tamaño del efecto

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Medida estadística de la magnitud de un fenómeno

En estadística, un tamaño del efecto es un valor que mide la fuerza de la relación entre dos variables en una población, o una estimación de esa cantidad basada en una muestra. Puede referirse al valor de una estadística calculada a partir de una muestra de datos, al valor de un parámetro para una población hipotética o a la ecuación que operacionaliza cómo las estadísticas o parámetros conducen al valor del tamaño del efecto. Ejemplos de tamaños del efecto incluyen la correlación entre dos variables, el coeficiente de regresión en una regresión, la diferencia de medias o el riesgo de que ocurra un evento particular (como un ataque cardíaco). Los tamaños del efecto complementan las pruebas de hipótesis estadísticas y desempeñan un papel importante en los análisis de poder, la planificación del tamaño de la muestra y los metanálisis. El conjunto de métodos de análisis de datos relativos a los tamaños del efecto se denomina estadística de estimación.

El tamaño del efecto es un componente esencial al evaluar la solidez de una afirmación estadística y es el primer elemento (magnitud) de los criterios MAGIC. La desviación estándar del tamaño del efecto es de importancia crítica, ya que indica cuánta incertidumbre se incluye en la medición. Una desviación estándar demasiado grande hará que la medición pierda casi sentido. En el metanálisis, donde el propósito es combinar múltiples tamaños del efecto, la incertidumbre en el tamaño del efecto se utiliza para sopesar los tamaños del efecto, de modo que los estudios grandes se consideran más importantes que los estudios pequeños. La incertidumbre en el tamaño del efecto se calcula de manera diferente para cada tipo de tamaño del efecto, pero generalmente solo requiere conocer el tamaño de la muestra del estudio (N), o el número de observaciones (n ) en cada grupo.

Informar los tamaños del efecto o sus estimaciones (estimación del efecto [EE], estimación del efecto) se considera una buena práctica al presentar los resultados de investigaciones empíricas en muchos campos. La presentación de informes sobre los tamaños del efecto facilita la interpretación de la importancia de un resultado de investigación, en contraste con su significación estadística. Los tamaños del efecto son particularmente prominentes en las ciencias sociales y en la investigación médica (donde el tamaño del efecto del tratamiento es importante).

Los tamaños del efecto pueden medirse en términos relativos o absolutos. En los tamaños relativos del efecto, dos grupos se comparan directamente entre sí, como en los odds ratios y los riesgos relativos. Para tamaños de efecto absolutos, un valor absoluto mayor siempre indica un efecto más fuerte. Muchos tipos de medidas se pueden expresar como absolutas o relativas, y se pueden utilizar juntas porque transmiten información diferente. Un destacado grupo de trabajo de la comunidad de investigación en psicología hizo la siguiente recomendación:

Siempre presentan tamaños de efecto para los resultados primarios... Si las unidades de medición son significativas en un nivel práctico (por ejemplo, el número de cigarrillos ahumados por día), entonces normalmente preferimos una medida no estandarizada (coeficiente de regresión o diferencia media) a una medida estandarizada (r o d).

Descripción general

Tamaños del efecto de población y muestra

Al igual que en la estimación estadística, el verdadero tamaño del efecto se distingue del tamaño del efecto observado, por ejemplo para medir el riesgo de enfermedad en una población (el tamaño del efecto de la población) se puede medir el riesgo dentro de una muestra de esa población (el tamaño del efecto muestral). Convenciones para describir los tamaños de los efectos verdaderos y observados siguen prácticas estadísticas estándar: un enfoque común es utilizar letras griegas como ρ [rho] para denotar parámetros de población y letras latinas como r para denotar la estadística correspondiente. Alternativamente, un "hat" se puede colocar sobre el parámetro de población para denotar la estadística, por ejemplo con ${hat {rho }}$ siendo la estimación del parámetro $rho$ .

Como en cualquier entorno estadístico, los tamaños del efecto se estiman con error de muestreo y pueden estar sesgados a menos que el estimador del tamaño del efecto que se utilice sea apropiado para la forma en que se muestrearon los datos y la forma en que se realizaron las mediciones. Un ejemplo de esto es el sesgo de publicación, que ocurre cuando los científicos informan resultados solo cuando los tamaños del efecto estimados son grandes o estadísticamente significativos. Como resultado, si muchos investigadores llevan a cabo estudios con bajo poder estadístico, los tamaños del efecto informados tenderán a ser mayores que los efectos reales (poblacionales), si los hay. Otro ejemplo en el que los tamaños del efecto pueden estar distorsionados es en un experimento de múltiples ensayos, donde el cálculo del tamaño del efecto se basa en la respuesta promediada o agregada entre los ensayos.

Los estudios más pequeños a veces muestran tamaños de efecto diferentes, a menudo más grandes, que los estudios más grandes. Este fenómeno se conoce como efecto de estudio pequeño, que puede indicar un sesgo de publicación.

Relación con las estadísticas de prueba

Los tamaños del efecto basados en muestras se distinguen de las estadísticas de prueba utilizadas en las pruebas de hipótesis, en que estiman la fuerza (magnitud) de, por ejemplo, una relación aparente, en lugar de asignar un nivel de significancia que refleje si la magnitud de la relación observada podría deberse al azar. El tamaño del efecto no determina directamente el nivel de significancia, ni viceversa. Dado un tamaño de muestra suficientemente grande, una comparación estadística no nula siempre mostrará un resultado estadísticamente significativo a menos que el tamaño del efecto poblacional sea exactamente cero (e incluso allí mostrará significancia estadística a la tasa del error Tipo I utilizado). Por ejemplo, un coeficiente de correlación de Pearson de muestra de 0,01 es estadísticamente significativo si el tamaño de la muestra es 1000. Informar sólo el valor p significativo de este análisis podría ser engañoso si una correlación de 0,01 es demasiado pequeña para ser de interés en una aplicación particular.

Tamaños de efecto estandarizados y no estandarizados

El término tamaño del efecto puede referirse a una medida estandarizada del efecto (como la r, la d de Cohen o el odds ratio) o a una medida no estandarizada. medida (por ejemplo, la diferencia entre las medias del grupo o los coeficientes de regresión no estandarizados). Las medidas estandarizadas del tamaño del efecto se suelen utilizar cuando:

las métricas de las variables estudiadas no tienen significado intrínseco (por ejemplo, una puntuación en una prueba de personalidad a escala arbitraria),
resultados de múltiples estudios se están combinando,
algunos o todos los estudios utilizan diferentes escalas, o
se desea transmitir el tamaño de un efecto relativo a la variabilidad de la población.

En los metanálisis, los tamaños del efecto estandarizados se utilizan como una medida común que se puede calcular para diferentes estudios y luego combinarse en un resumen general.

Interpretación

El hecho de que el tamaño de un efecto deba interpretarse como pequeño, mediano o grande depende de su contexto sustantivo y su definición operativa. Los criterios convencionales de Cohen pequeño, mediano o grande son casi omnipresentes en muchos campos, aunque Cohen advirtió:

"Los términos 'pequeño,' 'medio,' y 'grande' son relativos, no sólo entre sí, sino al área de la ciencia conductual o incluso más particularmente al contenido específico y método de investigación que se emplea en cualquier investigación dada.... Frente a esta relatividad, existe cierto riesgo inherente a ofrecer definiciones operacionales convencionales para estos términos para su uso en el análisis de poder en un campo tan diverso de investigación como la ciencia conductual. Sin embargo, este riesgo se acepta en la creencia de que hay que ganar más que perder proporcionando un marco convencional común de referencia que se recomienda utilizar sólo cuando no hay mejor base para estimar el índice ES disponible." (pág. 25)

En el diseño de dos muestras, Sawilowsky concluyó: "Con base en los hallazgos de las investigaciones actuales en la literatura aplicada, parece apropiado revisar las reglas generales para los tamaños del efecto", dijo. teniendo en cuenta las advertencias de Cohen y amplió las descripciones para incluir muy pequeño, muy grande y enorme. Se podrían desarrollar las mismas normas de facto para otros diseños.

Lenth destaca por un tamaño "medio" tamaño del efecto, "usted elegirá el mismo n independientemente de la precisión o confiabilidad de su instrumento, o de la estrechez o diversidad de sus sujetos. Es evidente que aquí se ignoran consideraciones importantes. Los investigadores deben interpretar la importancia sustancial de sus resultados basándose en un contexto significativo o cuantificando su contribución al conocimiento, y las descripciones del tamaño del efecto de Cohen pueden ser útiles como punto de partida. De manera similar, un informe patrocinado por el Departamento de Educación de EE. UU. decía: "El uso indiscriminado y generalizado de los valores genéricos de tamaño del efecto pequeño, mediano y grande de Cohen para caracterizar los tamaños del efecto en dominios a los que sus valores normativos no se aplican es igualmente inapropiado y engañoso".."

Sugirieron que "las normas apropiadas son aquellas basadas en distribuciones de tamaños de efectos para medidas de resultados comparables de intervenciones comparables dirigidas a muestras comparables". Por lo tanto, si un estudio en un campo donde la mayoría de las intervenciones son pequeñas arroja un efecto pequeño (según los criterios de Cohen), estos nuevos criterios lo llamarían "grande". En un punto relacionado, véase la paradoja de Abelson y la paradoja de Sawilowsky.

Tipos

Se conocen entre 50 y 100 medidas diferentes del tamaño del efecto. Muchos tamaños de efectos de diferentes tipos se pueden convertir a otros tipos, ya que muchos estiman la separación de dos distribuciones, por lo que están relacionados matemáticamente. Por ejemplo, un coeficiente de correlación se puede convertir a la d de Cohen y viceversa.

Did you mean:

Correlation family: Effect sizes based on "variance explained#34;

Did you mean:

These effect sizes estimate the amount of the variance within an experiment that is "explained or#34; or "accounted for" by the experiment 's model (Explained variation).

Pearson r o coeficiente de correlación

La correlación de Pearson, a menudo denominada r e introducida por Karl Pearson, se utiliza ampliamente como un tamaño del efecto cuando se dispone de datos cuantitativos pareados; por ejemplo, si estuviéramos estudiando la relación entre el peso al nacer y la longevidad. El coeficiente de correlación también se puede utilizar cuando los datos son binarios. La r de Pearson puede variar en magnitud de −1 a 1, donde −1 indica una relación lineal negativa perfecta, 1 indica una relación lineal positiva perfecta y 0 indica que no hay relación lineal entre dos variables.. Cohen da las siguientes pautas para las ciencias sociales:

Tamaño del efecto	r
Pequeña	0.10
Mediana	0.30
Grande	0,50

Coeficiente de determinación (r2 o R2)

Un tamaño del efecto relacionado es r², el coeficiente de determinación (también conocido como R² o "r-cuadrado"), calculado como el cuadrado de la correlación de Pearson r. En el caso de datos pareados, esta es una medida de la proporción de varianza compartida por las dos variables y varía de 0 a 1. Por ejemplo, con un r de 0,21 el coeficiente de determinación es 0,0441, lo que significa que el 4,4% de la varianza de cualquiera de las variables se comparte con la otra variable. El r² es siempre positivo, por lo que no transmite la dirección de la correlación entre las dos variables.

Eta-cuadrado (η2)

Eta-cuadrado describe la proporción de varianza explicada en la variable dependiente por un predictor mientras se controlan otros predictores, lo que lo hace análogo al r². Eta-cuadrado es un estimador sesgado de la varianza explicada por el modelo en la población (estima solo el tamaño del efecto en la muestra). Esta estimación comparte la debilidad con r² de que cada variable adicional aumentará automáticamente el valor de η². Además, mide la varianza explicada de la muestra, no de la población, lo que significa que siempre sobreestimará el tamaño del efecto, aunque el sesgo se reduce a medida que la muestra crece.

{displaystyle eta ^{2}={frac {SS_{text{Treatment}}}{SS_{text{Total}}}}.}

Omega cuadrado (ω2)

Un estimador menos sesgado de la varianza explicada en la población es ω²

{displaystyle omega ^{2}={frac {{text{SS}}_{text{treatment}}-df_{text{treatment}}cdot {text{MS}}_{text{error}}}{{text{SS}}_{text{total}}+{text{MS}}_{text{error}}}}.}

Esta forma de fórmula se limita al análisis entre sujetos con tamaños de muestra iguales en todas las celdas. Dado que es menos sesgado (aunque no unsesgado), ω² es preferible a η²; sin embargo, puede resultar más inconveniente calcularlo para análisis complejos. Se ha publicado una forma generalizada del estimador para experimentos de análisis entre sujetos y dentro de sujetos, medidas repetidas, diseño mixto y diseño de bloques aleatorios. Además, se han publicado métodos para calcular ω² parcial para factores individuales y factores combinados en diseños con hasta tres variables independientes.

Did you mean:

Cohen 's f2

La f² de Cohen es una de varias medidas del tamaño del efecto que se pueden utilizar en el contexto de una prueba F para ANOVA o regresión múltiple. Su cantidad de sesgo (sobreestimación del tamaño del efecto para el ANOVA) depende del sesgo de su medida subyacente de la varianza explicada (por ejemplo, R², η², ω²).

La medida del tamaño del efecto f² para la regresión múltiple se define como:

{displaystyle f^{2}={R^{2} over 1-R^{2}}}

R²

Asimismo, f² se puede definir como:

{displaystyle f^{2}={eta ^{2} over 1-eta ^{2}}}

{displaystyle f^{2}={omega ^{2} over 1-omega ^{2}}}

El $f^{2}$ medida de tamaño de efecto para la regresión múltiple secuencial y también común para el modelado PLS se define como:

{displaystyle f^{2}={R_{AB}^{2}-R_{A}^{2} over 1-R_{AB}^{2}}}

R²_AAR²_ABABf²

{displaystyle 0.1^{2}}

{displaystyle 0.25^{2}}

{displaystyle 0.4^{2}}

pequeñomedianogrande

Cohen's ${hat {f}}$ también se puede encontrar para el análisis factorial de la varianza (ANOVA) trabajando hacia atrás, utilizando:

{displaystyle {hat {f}}_{text{effect}}={sqrt {(F_{text{effect}}df_{text{effect}}/N)}}.}

En un diseño equilibrado (tamaños de muestra equivalentes en grupos) de ANOVA, el parámetro de población correspondiente $f^{2}$ es

{displaystyle {SS(mu _{1},mu _{2},dotsmu _{K})} over {Ktimes sigma ^{2}},}

μ_jj^TKσSS

Did you mean:

Cohen 's q

Did you mean:

Another measure that is used with correlation differences is Cohen 's q. This is the difference between two Fisher transformed Pearson regression coefficients. In symbols this is

{displaystyle q={frac {1}{2}}log {frac {1+r_{1}}{1-r_{1}}}-{frac {1}{2}}log {frac {1+r_{2}}{1-r_{2}}}}

donde r₁ y r₂ son las regresiones que se comparan. El valor esperado de q es cero y su varianza es

{displaystyle operatorname {var} (q)={frac {1}{N_{1}-3}}+{frac {1}{N_{2}-3}}}

N₁N₂

Familia de diferencias: tamaños del efecto basados en diferencias entre medias

El tamaño del efecto bruto correspondiente a una comparación de dos grupos se calcula inherentemente como las diferencias entre las dos medias. Sin embargo, para facilitar la interpretación es común estandarizar el tamaño del efecto; A continuación se presentan varias convenciones para la estandarización estadística.

Diferencia de medias estandarizada

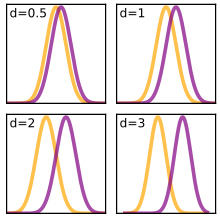
Un tamaño del efecto (poblacional) θ basado en medias generalmente considera la diferencia de medias estandarizada (DME) entre dos poblaciones.

{displaystyle theta ={frac {mu _{1}-mu _{2}}{sigma }},}

μ₁μ₂

En el entorno práctico, los valores de la población generalmente no se conocen y deben estimarse a partir de estadísticas de muestra. Las diversas versiones de tamaños del efecto basadas en medias difieren con respecto a las estadísticas que se utilizan.

Esta forma para el tamaño del efecto se asemeja a la computación para una estadística t-test, con la diferencia crítica que la t-La estadística más reciente incluye un factor ${sqrt {n}}$ . Esto significa que para un tamaño de efecto dado, el nivel de significación aumenta con el tamaño de la muestra. A diferencia de t-prueba estadística, el tamaño del efecto tiene como objetivo estimar un parámetro de población y no se ve afectado por el tamaño de la muestra.

Los valores de SMD de 0,2 a 0,5 se consideran pequeños, de 0,5 a 0,8 se consideran medios y mayores de 0,8 se consideran grandes.

Did you mean:

Cohen 's d

Did you mean:

Cohen 's d is defined as the difference between two means divided by a standard deviation for the data, i.e.

{displaystyle d={frac {{bar {x}}_{1}-{bar {x}}_{2}}{s}}.}

Jacob Cohen definió s, la desviación estándar agrupada, como (para dos muestras independientes):

{displaystyle s={sqrt {frac {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1}+n_{2}-2}}}}

{displaystyle s_{1}^{2}={frac {1}{n_{1}-1}}sum _{i=1}^{n_{1}}(x_{1,i}-{bar {x}}_{1})^{2},}

La siguiente tabla contiene descriptores para magnitudes de d = 0,01 a 2,0, como lo sugirió inicialmente Cohen y lo amplió Sawilowsky.

Tamaño del efecto	d	Referencia
Muy pequeño	0,01
Pequeña	0.20
Mediana	0,50
Grande	0.80
Muy grande	1.20
Huge	2.0

Did you mean:

Other authors choose a slightly different computation of the standard deviation when referring to "Cohen 's d" where the denominator is without "-2"

{displaystyle s={sqrt {frac {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1}+n_{2}}}}}

Con dos muestras pareadas, observamos la distribución de las puntuaciones de diferencia. En ese caso, s es la desviación estándar de esta distribución de puntuaciones de diferencia. Esto crea la siguiente relación entre el estadístico t para probar una diferencia en las medias de los dos grupos y el d de Cohen:

{displaystyle t={frac {{bar {X}}_{1}-{bar {X}}_{2}}{text{SE}}}={frac {{bar {X}}_{1}-{bar {X}}_{2}}{frac {text{SD}}{sqrt {N}}}}={frac {{sqrt {N}}({bar {X}}_{1}-{bar {X}}_{2})}{SD}}}

{displaystyle d={frac {{bar {X}}_{1}-{bar {X}}_{2}}{text{SD}}}={frac {t}{sqrt {N}}}}

La d de Cohen se utiliza con frecuencia para estimar tamaños de muestra para pruebas estadísticas. Un d de Cohen más bajo indica la necesidad de tamaños de muestra más grandes, y viceversa, como se puede determinar posteriormente junto con los parámetros adicionales del nivel de significancia deseado y el poder estadístico.

Para muestras pareadas, Cohen sugiere que la d calculada es en realidad una d', lo que no proporciona la respuesta correcta para obtener la potencia de la prueba, y que antes de buscar los valores en las tablas proporcionadas, debe corregirse para r como en la siguiente fórmula:

{displaystyle d={frac {d'}{sqrt {1-r}}}}

Did you mean:

Glass ' Δ

En 1976, Gene V. Glass propuso un estimador del tamaño del efecto que utiliza sólo la desviación estándar del segundo grupo.

{displaystyle Delta ={frac {{bar {x}}_{1}-{bar {x}}_{2}}{s_{2}}}}

El segundo grupo puede considerarse como un grupo de control, y Glass argumentó que si se compararan varios tratamientos con el grupo de control, sería mejor usar solo la desviación estándar calculada a partir del grupo de control, de modo que los tamaños del efecto no difieran. bajo iguales medias y diferentes varianzas.

Bajo un supuesto correcto de varianzas poblacionales iguales, una estimación agrupada para σ es más precisa.

Did you mean:

Hedges ' g

Did you mean:

Hedges ' g, suggested by Larry Hedges in 1981, is like the other measures based on a standardized difference

{displaystyle g={frac {{bar {x}}_{1}-{bar {x}}_{2}}{s^{*}}}}

s^{*}

{displaystyle s^{*}={sqrt {frac {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1}+n_{2}-2}}}.}

Sin embargo, como estimador del tamaño del efecto poblacional θ está sesgado. Sin embargo, este sesgo se puede corregir aproximadamente multiplicando por un factor

{displaystyle g^{*}=J(n_{1}+n_{2}-2),,g,approx ,left(1-{frac {3}{4(n_{1}+n_{2})-9}}right),,g}

g^{*}

ddJ

{displaystyle J(a)={frac {Gamma (a/2)}{{sqrt {a/2,}},Gamma ((a-1)/2)}}.}

Ψ, efecto estandarizado de raíz cuadrática media

Did you mean:

A similar effect size estimator for multiple comparisons (i.n., ANOVA) is the Ψ root-mean-square standardized effect:

{displaystyle Psi ={sqrt {{frac {1}{k-1}}cdot sum _{j=1}^{k}left({frac {mu _{j}-mu }{sigma }}right)^{2}}}}

Esto esencialmente presenta la diferencia general de todo el modelo ajustada por la raíz cuadrática media, análoga a d o g.

Además, se ha proporcionado una generalización para diseños multifactoriales.

Distribución de los tamaños del efecto según las medias

Siempre que los datos sean Gaussian distribuidos un Hedges escalado ' g, ${textstyle {sqrt {n_{1}n_{2}/(n_{1}+n_{2})}},g}$ , sigue una distribución t no central con el parámetro no central ${textstyle {sqrt {n_{1}n_{2}/(n_{1}+n_{2})}}theta }$ y $() n 1 + n 2 - 2)$ grados de libertad. Del mismo modo, el vidrio escalado Δ se distribuye con $n 2 - 1$ grados de libertad.

A partir de la distribución es posible calcular la expectativa y la varianza de los tamaños del efecto.

Did you mean:

In some cases large sample approximations for the variance are used. One suggestion for the variance of Hedges ' unbiased estimator is

{displaystyle {hat {sigma }}^{2}(g^{*})={frac {n_{1}+n_{2}}{n_{1}n_{2}}}+{frac {(g^{*})^{2}}{2(n_{1}+n_{2})}}.}

Otras métricas

Did you mean:

Mahalanobis distance (D) is a multivariate generalization of Cohen 's d, which takes into account the relationships between the variables.

Familia categórica: tamaños del efecto para asociaciones entre variables categóricas

Phiφ)	Cramér V ()φ_c)
${displaystyle varphi ={sqrt {frac {chi ^{2}}{N}}}}$	${displaystyle varphi _{c}={sqrt {frac {chi ^{2}}{N(k-1)}}}}$

Las medidas de asociación comúnmente utilizadas para la prueba de chi-cuadrado son el coeficiente Phi y la V de Cramér (a veces denominada phi de Cramér y denotada como φ_c). Phi está relacionado con el coeficiente de correlación biserial puntual y el d de Cohen y estima el alcance de la relación entre dos variables (2 × 2). La V de Cramér se puede utilizar con variables que tengan más de dos niveles.

Phi se puede calcular encontrando la raíz cuadrada del estadístico chi-cuadrado dividida por el tamaño de la muestra.

De manera similar, la V de Cramér se calcula tomando la raíz cuadrada del estadístico chi-cuadrado dividida por el tamaño de la muestra y la longitud de la dimensión mínima (k es el menor de los número de filas r o columnas c).

φ_c es la intercorrelación de las dos variables discretas y puede calcularse para cualquier valor de r o c. Sin embargo, como los valores de chi-cuadrado tienden a aumentar con el número de celdas, cuanto mayor sea la diferencia entre r y c, es más probable que V tienda a 1 sin evidencia sólida. de una correlación significativa.

Did you mean:

Cohen 's omega (ω)

Otra medida del tamaño del efecto utilizado para las pruebas de la piel es la omega de Cohen ( $omega$ ). Esto se define como

{displaystyle omega ={sqrt {sum _{i=1}^{m}{frac {(p_{1i}-p_{0i})^{2}}{p_{0i}}}}}}

p_0ii^TH₀p_1ii^TH₁m

En Análisis de poder estadístico para las ciencias del comportamiento (1988, pp.224-225), Cohen da la siguiente pauta general para interpretar omega (ver tabla a continuación), pero advierte contra su "posible incapacidad en cualquier contexto sustantivo dado" y aconseja utilizar en su lugar un juicio relevante para el contexto.

Tamaño del efecto	$omega$
Pequeña	0.10
Mediana	0.30
Grande	0,50

Ratio de probabilidades

El odds ratio (OR) es otro tamaño del efecto útil. Es apropiado cuando la pregunta de investigación se centra en el grado de asociación entre dos variables binarias. Por ejemplo, considere un estudio sobre la capacidad de ortografía. En un grupo de control, dos estudiantes aprueban la clase por cada uno que reprueba, por lo que las probabilidades de aprobar son de dos a uno (o 2/1 = 2). En el grupo de tratamiento, seis estudiantes aprueban por cada uno que reprueba, por lo que las probabilidades de aprobar son de seis a uno (o 6/1 = 6). El tamaño del efecto se puede calcular observando que las probabilidades de aprobar en el grupo de tratamiento son tres veces mayores que en el grupo de control (porque 6 dividido por 2 es 3). Por lo tanto, el odds ratio es 3. Las estadísticas del odds ratio están en una escala diferente a la d de Cohen, por lo que este '3' no es comparable a una d de Cohen de 3.

Riesgo relativo

El riesgo relativo (RR), también llamado razón de riesgo, es simplemente el riesgo (probabilidad) de un evento en relación con alguna variable independiente. Esta medida del tamaño del efecto difiere del odds ratio en que compara probabilidades en lugar de odds, pero se aproxima asintóticamente a esta última para probabilidades pequeñas. Usando el ejemplo anterior, las probabilidades de que pasen los del grupo de control y del grupo de tratamiento son 2/3 (o 0,67) y 6/7 (o 0,86), respectivamente. El tamaño del efecto se puede calcular igual que antes, pero utilizando las probabilidades. Por tanto, el riesgo relativo es 1,28. Dado que se utilizaron probabilidades de aprobación bastante grandes, existe una gran diferencia entre el riesgo relativo y el odds ratio. Si se hubiera utilizado fracaso (una probabilidad menor) como evento (en lugar de aprobar), la diferencia entre las dos medidas del tamaño del efecto no sería tan grande.

Si bien ambas medidas son útiles, tienen diferentes usos estadísticos. En la investigación médica, el odds ratio se utiliza comúnmente para estudios de casos y controles, ya que generalmente se estiman los odds, pero no las probabilidades. El riesgo relativo se utiliza comúnmente en ensayos controlados aleatorios y estudios de cohortes, pero el riesgo relativo contribuye a sobreestimaciones de la efectividad de las intervenciones.

Diferencia de riesgo

La diferencia de riesgo (DR), a veces llamada reducción absoluta del riesgo, es simplemente la diferencia en el riesgo (probabilidad) de un evento entre dos grupos. Es una medida útil en la investigación experimental, ya que la RD indica en qué medida una intervención experimental cambia la probabilidad de un evento o resultado. Usando el ejemplo anterior, las probabilidades de que aquellos en el grupo de control y en el grupo de tratamiento aprueben son 2/3 (o 0,67) y 6/7 (o 0,86), respectivamente, por lo que el tamaño del efecto RD es 0,86 − 0,67 = 0,19 (o 19%). RD es la medida superior para evaluar la efectividad de las intervenciones.

Did you mean:

Cohen 's h

Did you mean:

One measure used in power analysis when comparing two independent proportions is Cohen 's h. This is defined as follows

{displaystyle h=2(arcsin {sqrt {p_{1}}}-arcsin {sqrt {p_{2}}})}

p₁p₂

Tamaño del efecto del lenguaje común

Para describir más fácilmente el significado de un tamaño del efecto a personas ajenas a la estadística, el tamaño del efecto en lenguaje común, como su nombre lo indica, fue diseñado para comunicarlo en un inglés sencillo. Se utiliza para describir una diferencia entre dos grupos y fue propuesto, además de nombrado, por Kenneth McGraw y S. P. Wong en 1992. Utilizaron el siguiente ejemplo (sobre las alturas de hombres y mujeres): "en cualquier emparejamiento aleatorio de hombres y mujeres adultos jóvenes, la probabilidad de que el hombre sea más alto que la mujer es 92, o en términos más simples aún, en 92 de cada 100 citas a ciegas entre adultos jóvenes, el hombre será más alto que la mujer", al describir el valor poblacional del tamaño del efecto del lenguaje común.

El valor poblacional, para el tamaño del efecto del lenguaje común, a menudo se informa así, en términos de pares elegidos aleatoriamente de la población. Kerby (2014) señala que un par, definido como una puntuación en un grupo emparejada con una puntuación en otro grupo, es un concepto central del tamaño del efecto del lenguaje común.

Como otro ejemplo, considere un estudio científico (tal vez de un tratamiento para alguna enfermedad crónica, como la artritis) con diez personas en el grupo de tratamiento y diez personas en un grupo de control. Si se compara a todos los miembros del grupo de tratamiento con todos los del grupo de control, entonces hay (10×10=) 100 pares. Al final del estudio, el resultado se clasifica en una puntuación para cada individuo (por ejemplo, en una escala de movilidad y dolor, en el caso de un estudio de artritis) y luego se comparan todas las puntuaciones entre los pares. El resultado, como porcentaje de pares que apoyan la hipótesis, es el tamaño del efecto del lenguaje común. En el estudio de ejemplo podría ser (digamos) 80, si 80 de los 100 pares de comparación muestran un mejor resultado para el grupo de tratamiento que para el grupo de control, y el informe podría decir lo siguiente: "Cuando se comparó a un paciente del grupo de tratamiento con un paciente del grupo de control, en 80 de 100 pares el paciente tratado mostró un mejor resultado del tratamiento". El valor de la muestra, por ejemplo en un estudio como este, es un estimador insesgado del valor de la población.

Vargha y Delaney generalizaron el tamaño del efecto del lenguaje común (Vargha-Delaney A), para cubrir datos de nivel ordinal.

Correlación rango-biserial

Un tamaño del efecto relacionado con el tamaño del efecto del lenguaje común es la correlación de rango biserial. Esta medida fue introducida por Cureton como tamaño del efecto para la prueba U de Mann-Whitney. Es decir, hay dos grupos y las puntuaciones de los grupos se han convertido en rangos. La fórmula de diferencia simple de Kerby calcula la correlación biserial de rango a partir del tamaño del efecto del lenguaje común. Sea f la proporción de pares favorables a la hipótesis (el tamaño del efecto del lenguaje común), y sea u la proporción de pares no favorables, el rango biserial r es la diferencia simple entre las dos proporciones: r = f − u. En otras palabras, la correlación es la diferencia entre el tamaño del efecto del lenguaje común y su complemento. Por ejemplo, si el tamaño del efecto del lenguaje común es 60 %, entonces el rango biserial r es igual a 60 % menos 40 %, o r = 0,20. La fórmula de Kerby es direccional y los valores positivos indican que los resultados respaldan la hipótesis.

Wendt proporcionó una fórmula no direccional para la correlación biserial de rango, de modo que la correlación siempre es positiva. La ventaja de la fórmula de Wendt es que se puede calcular con información que está fácilmente disponible en artículos publicados. La fórmula utiliza solo el valor de prueba de U de la prueba U de Mann-Whitney y los tamaños de muestra de los dos grupos: r = 1 – (2U)/(n₁ n₂). Tenga en cuenta que U se define aquí según la definición clásica como el menor de los dos valores U que se pueden calcular a partir de los datos. Esto garantiza que 2U < n₁n₂, como n₁ n₂ es el valor máximo de las estadísticas U.

Un ejemplo puede ilustrar el uso de las dos fórmulas. Consideremos un estudio de salud de veinte adultos mayores, diez en el grupo de tratamiento y diez en el grupo de control; por tanto, hay diez veces diez o 100 pares. El programa de salud utiliza dieta, ejercicio y suplementos para mejorar la memoria, y la memoria se mide mediante una prueba estandarizada. Una prueba U de Mann-Whitney muestra que el adulto del grupo de tratamiento tenía mejor memoria en 70 de los 100 pares y peor memoria en 30 pares. La U de Mann-Whitney es la menor entre 70 y 30, por lo que U = 30. La correlación entre la memoria y el rendimiento del tratamiento según la fórmula de diferencia simple de Kerby es r = (70/100) − (30/100) = 0,40. La correlación según la fórmula de Wendt es r = 1 − (2·30)/(10·10) = 0,40.

Tamaño del efecto para datos ordinales

Cliff's delta o $d$ , desarrollado originalmente por Norman Cliff para su uso con datos ordinal, es una medida de cuán a menudo los valores en una distribución son mayores que los valores en una segunda distribución. Curiosamente, no requiere ninguna suposición sobre la forma o difusión de las dos distribuciones.

Estimación de la muestra $d$ es dado por:

x_{j}]-[x_{i}d=.. i,j[xi■xj]− − [xi.xj]mn{displaystyle d={frac {sum _{i,0} [x_{i} {mn}}x_{j}]-[x_{i}

n

m

x_{i}

x_{j}

{displaystyle [cdot ]}

$d$ se relaciona linealmente con la estadística Mann-Whitney U; sin embargo, capta la dirección de la diferencia en su signo. Dada la Mann-Whitney $U$ , $d$ es:

{displaystyle d={frac {2U}{mn}}-1}

Intervalos de confianza mediante parámetros de no centralidad

Intervalos de confianza de tamaños de efecto estandarizados, especialmente Cohen ${d}$ y $f^{2}$ , confíe en el cálculo de intervalos de confianza de parámetros no centrales (Ncp). Un enfoque común para construir el intervalo de confianza Ncp es encontrar el crítico Ncp valores para adaptarse a la estadística observada a quantiles de cola α/2 y (1 −α/2). El MBESS SAS y R-package ofrece funciones para encontrar valores críticos Ncp.

Prueba T para la diferencia de medias de un solo grupo o dos grupos relacionados

Para un solo grupo, M denota la media de la muestra, μ la media de la población, SD la desviación estándar de la muestra, σ es la desviación estándar de la población y n es el tamaño de la muestra del grupo. El valor t se utiliza para probar la hipótesis sobre la diferencia entre la media y una línea base μ_{línea base}. Por lo general, μ_{línea de base} es cero. En el caso de dos grupos relacionados, el grupo único se construye mediante las diferencias en pares de muestras, mientras que SD y σ denotan la muestra y la población.;s desviaciones estándar de las diferencias en lugar de dentro de los dos grupos originales.

{displaystyle t:={frac {M-mu _{text{baseline}}}{text{SE}}}={frac {M-mu _{text{baseline}}}{{text{SD}}/{sqrt {n}}}}={frac {{sqrt {n}}left({frac {M-mu }{sigma }}right)+{sqrt {n}}left({frac {mu -mu _{text{baseline}}}{sigma }}right)}{frac {text{SD}}{sigma }}}}

{displaystyle ncp={sqrt {n}}left({frac {mu -mu _{text{baseline}}}{sigma }}right)}

{displaystyle d:={frac {M-mu _{text{baseline}}}{text{SD}}}}

es la estimación puntual de

{displaystyle {frac {mu -mu _{text{baseline}}}{sigma }}.}

Entonces,

{displaystyle {tilde {d}}={frac {ncp}{sqrt {n}}}.}

Prueba T para la diferencia de medias entre dos grupos independientes

n₁ o n₂ son los tamaños de muestra respectivos.

{displaystyle t:={frac {M_{1}-M_{2}}{{text{SD}}_{text{within}}/{sqrt {frac {2*n_{1}n_{2}}{n_{1}+n_{2}}}}}},}

Did you mean:

where

{displaystyle {text{SD}}_{text{within}}:={sqrt {frac {{text{SS}}_{text{within}}}{{text{df}}_{text{within}}}}}={sqrt {frac {(n_{1}-1){text{SD}}_{1}^{2}+(n_{2}-1){text{SD}}_{2}^{2}}{n_{1}+n_{2}-2}}}.}

{displaystyle ncp={sqrt {frac {n_{1}n_{2}}{n_{1}+n_{2}}}}{frac {mu _{1}-mu _{2}}{sigma }}}

Did you mean:

and Cohen 's

{displaystyle d:={frac {M_{1}-M_{2}}{SD_{text{within}}}}}

{displaystyle {frac {mu _{1}-mu _{2}}{sigma }}.}

Entonces,

{displaystyle {tilde {d}}={frac {ncp}{sqrt {frac {n_{1}n_{2}}{n_{1}+n_{2}}}}}.}

Prueba ANOVA unidireccional para la diferencia de medias entre múltiples grupos independientes

La prueba ANOVA de un solo sentido se aplica a la distribución F no central. Mientras que con una determinada desviación estándar de la población $sigma$ , la misma pregunta de prueba aplica la distribución no central de chi-squared.

{displaystyle F:={frac {{frac {{text{SS}}_{text{between}}}{sigma ^{2}}}/{text{df}}_{text{between}}}{{frac {{text{SS}}_{text{within}}}{sigma ^{2}}}/{text{df}}_{text{within}}}}}

Para cada j-ésima muestra dentro del i-ésimo grupo X_i,j, denota

{displaystyle M_{i}(X_{i,j}):={frac {sum _{w=1}^{n_{i}}X_{i,w}}{n_{i}}};;mu _{i}(X_{i,j}):=mu _{i}.}

Mientras,

{displaystyle {begin{aligned}{text{SS}}_{text{between}}/sigma ^{2}&={frac {{text{SS}}left(M_{i}(X_{i,j});i=1,2,dotsK,;j=1,2,dotsn_{i}right)}{sigma ^{2}}}\&={text{SS}}left({frac {M_{i}(X_{i,j}-mu _{i})}{sigma }}+{frac {mu _{i}}{sigma }};i=1,2,dotsK,;j=1,2,dotsn_{i}right)\&sim chi ^{2}left({text{df}}=K-1,;ncp=SSleft({frac {mu _{i}(X_{i,j})}{sigma }};i=1,2,dotsK,;j=1,2,dotsn_{i}right)right)end{aligned}}}

Así que, ambos. Ncp()s) de F y $chi ^{2}$ equate

{displaystyle {text{SS}}left(mu _{i}(X_{i,j})/sigma;i=1,2,dotsK,;j=1,2,dotsn_{i}right).}

En caso de $n:=n_{1}=n_{2}=cdots =n_{K}$ para K grupos independientes del mismo tamaño, el tamaño total de la muestra es N:=n·K.

{displaystyle {text{Cohens }}{tilde {f}}^{2}:={frac {{text{SS}}(mu _{1},mu _{2},dotsmu _{K})}{Kcdot sigma ^{2}}}={frac {{text{SS}}left(mu _{i}(X_{i,j})/sigma;i=1,2,dotsK,;j=1,2,dotsn_{i}right)}{ncdot K}}={frac {ncp}{ncdot K}}={frac {ncp}{N}}.}

El t-La prueba para un par de grupos independientes es un caso especial de ANOVA. Tenga en cuenta que el parámetro no central $ncp_{F}$ de F no es comparable al parámetro no central $ncp_{t}$ del correspondiente t. En realidad, ${displaystyle ncp_{F}=ncp_{t}^{2}}$ , y ${displaystyle {tilde {f}}=left|{frac {tilde {d}}{2}}right|}$ .

Contenido relacionado

Más resultados...