Tales de Mileto

Tales de Mileto (griego: Θαλῆς (ὁ Μιλήσιος), Thalēs; c. 624/623 - c. 548/545 a. C.) fue un matemático, astrónomo y filósofo presocrático griego de Mileto en Jonia, Asia Menor. Fue uno de los Siete Sabios de Grecia. Muchos, sobre todo Aristóteles, lo consideraban el primer filósofo de la tradición griega y, por lo demás, se le reconoce históricamente como el primer individuo del que se sabe que entretuvo y se comprometió con la filosofía científica. A menudo se le conoce como el Padre de la Ciencia.
Tales es reconocido por romper con el uso de la mitología para explicar el mundo y el universo y, en cambio, explicar los objetos y fenómenos naturales mediante teorías e hipótesis naturalistas, en un precursor de la ciencia moderna. Casi todos los demás filósofos presocráticos lo siguieron al explicar la naturaleza como derivada de una unidad de todo basada en la existencia de una única sustancia última, en lugar de utilizar explicaciones mitológicas. Aristóteles lo consideró como el fundador de la Escuela Jónica e informó la hipótesis de Tales de que el principio originario de la naturaleza y la naturaleza de la materia era una sola sustancia material: el agua.
En matemáticas, Tales usó la geometría para calcular las alturas de las pirámides y la distancia de los barcos a la costa. Es el primer individuo conocido en utilizar el razonamiento deductivo aplicado a la geometría, al derivar cuatro corolarios del teorema de Tales. Es el primer individuo conocido a quien se le ha atribuido un descubrimiento matemático.
Vida
Las fechas de la vida de Tales no se conocen exactamente, pero se establecen aproximadamente por algunos eventos datables mencionados en las fuentes. Según Heródoto, Tales predijo el eclipse solar del 28 de mayo de 585 a. Diogenes Laërtius cita la crónica de Apolodoro de Atenas diciendo que Tales murió a la edad de 78 años durante la 58.ª Olimpiada (548-545 a. C.) y atribuye su muerte a un golpe de calor mientras veía los juegos.
Tales probablemente nació en la ciudad de Mileto a mediados del 620 a. El antiguo escritor Apolodoro de Atenas, que escribió durante el siglo II a. C., pensó que Tales nació alrededor del año 625 a. C. Heródoto, escribiendo en el siglo V a. C., describió a Thales como "un fenicio de ascendencia remota". Sin embargo, lo más probable es que fuera tan griego como la mayoría de los milesios, ya que sus antepasados eran cadmeos de Beocia y no semitas. Tim Whitmarsh escribió que Thales consideraba el agua como la materia prima, y debido a que thal es la palabra fenicia para humedad, su nombre puede haber derivado de esta circunstancia.Sin embargo, esta parece ser una opinión minoritaria, ya que la mayoría de los diccionarios afirman que su nombre proviene de la palabra griega “θᾰ́λλω” (thállō, “prosperar”) + -ης (-ēs), en cuyo caso significa “uno que prospera”..
Según el historiador posterior Diógenes Laërtius, en su Vida de los filósofos del siglo III d. C., hace referencia a Herodoto, Duris y Demócrito, quienes todos están de acuerdo en que "Tales era hijo de Examyas y Cleobulina, y pertenecía a los Thelidae, que son fenicios y entre ellos". los más nobles descendientes de Cadmus y Agenor". Sus nombres son cario y griego, respectivamente. Friedrich Nietzsche enfatiza el hecho de que sus antepasados fueron solo "fenicios" en el sentido de que podrían rastrear sus orígenes ficticios hasta el pueblo marinero del héroe mitológico Cadmo. Por lo tanto, su familia emigró de Tebas, en el centro de Grecia, a Jonia en Asia Menor.Diógenes luego afirma que "la mayoría de los escritores, sin embargo, lo representan como un nativo de Mileto y de una familia distinguida". Su supuesta madre, Cleobulina, también ha sido descrita como su compañera en lugar de su madre. Sin embargo, el consenso académico es que, aunque algunos autores antiguos dicen que era de origen fenicio, lo más probable es que fuera un milesio nativo de noble cuna y que ciertamente era griego. Diógenes continúa entregando informes más contradictorios: uno que Tales se casó y tuvo un hijo (Cybisthus o Cybisthon) o adoptó a su sobrino del mismo nombre; el segundo que nunca se casó, diciéndole a su madre cuando era joven que era demasiado pronto para casarse, y cuando era mayor que era demasiado tarde. Plutarco había contado anteriormente esta versión: Solon visitó a Thales y le preguntó por qué seguía soltero; Tales respondió que no le gustaba la idea de tener que preocuparse por los niños. Sin embargo, varios años después, ansioso por tener una familia, adoptó a su sobrino Cybisthon.
Se supone que Tales, en un momento de su vida, visitó Egipto, donde aprendió geometría. No es imposible que Tales visitara Egipto, ya que Mileto tenía una colonia permanente allí (a saber, Naucratis), sin embargo, las visitas a Egipto fueron una atribución común a varios filósofos por parte de escritores posteriores, especialmente cuando estos escritores intentaron explicar el conocimiento matemático. Tales pudo haber sabido sobre Egipto por relatos de otros, sin haberlo visitado realmente. Diogenes Laërtius escribió que Tales identifica a Mileto como colonia ateniense.
Tales (que murió unos 30 años antes de la época de Pitágoras y 300 años antes que Euclides, Eudoxo de Cnido y Eudemo de Rodas) es a menudo aclamado como "el primer matemático griego". Si bien algunos historiadores, como Colin R. Fletcher, señalan que podría haber habido un antecesor de Tales que habría sido nombrado en el libro perdido de Eudemo Historia de la geometría, se admite que sin la obra “la cuestión se convierte en mera especulación. " Fletcher sostiene que, dado que no existe un predecesor viable para el título de primer matemático griego, la única pregunta es si Thales califica como un practicante en ese campo; sostiene que "Thales tenía a su disposición las técnicas de observación, experimentación, superposición y deducción... ha demostrado ser matemático.
Aristóteles escribió en Metafísica: "Thales, el fundador de esta escuela de filosofía, dice que la entidad permanente es el agua (por eso también propuso que la tierra flota sobre el agua). Presumiblemente, derivó esta suposición al ver que el alimento de todo es húmedo, y que el calor mismo se genera a partir de la humedad y depende de ella para su existencia (y aquello de lo que se genera una cosa es siempre su primer principio). Derivó su suposición de esto, y también del hecho de que las semillas de todo tienen una naturaleza húmeda, mientras que el agua es el primer principio de la naturaleza de las cosas húmedas".
Ocupaciones
Tales se involucró en muchas actividades, incluida la ingeniería. Algunos dicen que no dejó escritos. Otros dicen que escribió Sobre el solsticio y Sobre el equinoccio. Se le ha atribuido la guía de la estrella náutica, pero esto fue discutido en la antigüedad. No se ha conservado ningún escrito atribuido a él. Diógenes Laërtius cita dos cartas de Tales: una a Ferecides de Siros, en la que se ofrece a revisar su libro sobre religión, y otra a Solón, en la que se ofrece a hacerle compañía en su estancia en Atenas.
La historia de Olive como ejemplo de comercio de tipo opción
Una historia, con diferentes versiones, cuenta cómo Tales logró riquezas de una cosecha de aceitunas por la predicción del tiempo. En una versión, compró todas las prensas de aceitunas en Mileto después de predecir el clima y una buena cosecha para un año en particular. En otra versión de la historia, Aristóteles explica que Tales había reservado prensas por adelantado, con descuento, y podía alquilarlas a un precio alto cuando la demanda alcanzaba su punto máximo, siguiendo su predicción de una cosecha particularmente buena. Esta primera versión de la historia constituiría la primera creación y uso de futuros históricamente conocida, mientras que la segunda versión sería la primera creación y uso de opciones históricamente conocida.
Aristóteles explica que el objetivo de Tales al hacer esto no era enriquecerse sino demostrar a sus compañeros milesios que la filosofía podía ser útil, al contrario de lo que pensaban, o bien, Tales había hecho su incursión en la empresa debido a un desafío personal que se le había planteado. por un individuo que había preguntado por qué, si Tales era un famoso filósofo inteligente, aún no había alcanzado la riqueza.
Rol de asesor
Diógenes Laërtius nos dice que Tales ganó fama como consejero cuando aconsejó a los milesios que no se involucraran en una sinmaquia, una "lucha conjunta", con los lidios. Esto a veces se ha interpretado como una alianza. Otra historia de Herodoto es que Creso envió su ejército al territorio persa. Fue detenido por el río Halys, luego sin puente. Thales luego hizo que el ejército cruzara el río cavando un desvío río arriba para reducir el flujo, haciendo posible cruzar el río. Si bien Heródoto informó que la mayoría de sus compatriotas griegos creen que Tales desvió el río Halys para ayudar en los esfuerzos militares del rey Creso, él mismo lo encuentra dudoso.
Creso fue derrotado ante la ciudad de Sardis por Ciro, quien posteriormente perdonó a Mileto porque no había tomado ninguna medida. Ciro quedó tan impresionado por la sabiduría de Creso y su conexión con los sabios que lo perdonó y siguió su consejo en varios asuntos. Las ciudades jónicas deberían ser demoi, o "distritos".
Les aconsejó que establecieran una sola sede de gobierno y señaló a Teos como el lugar más adecuado para ello; "porque eso", dijo, "era el centro de Jonia. Sus otras ciudades aún podrían continuar disfrutando de sus propias leyes, como si fueran estados independientes".
Mileto, sin embargo, recibió condiciones favorables de Ciro. Los demás permanecieron en una Liga Jónica de doce ciudades (excluyendo Mileto), y fueron subyugados por los persas.
Astronomía
Según Heródoto, Tales predijo el eclipse solar del 28 de mayo de 585 a. Tales también describió la posición de la Osa Menor y pensó que la constelación podría ser útil como guía para la navegación en el mar. Calculó la duración del año y los tiempos de los equinoccios y solsticios. También se le atribuye la primera observación de las Híades y el cálculo de la posición de las Pléyades. Plutarco indica que en su época (c. 100 dC) existía una obra, la Astronomía, compuesta en verso y atribuida a Tales.
Herodoto escribe que en el sexto año de la guerra, los lidios bajo el mando del rey Alyattes y los medos bajo el mando de Ciaxares se vieron envueltos en una batalla indecisa cuando de repente el día se convirtió en noche, lo que llevó a ambas partes a detener la lucha y negociar un acuerdo de paz. Heródoto también menciona que Tales había predicho la pérdida de la luz del día. Sin embargo, no menciona el lugar de la batalla.
Después, por la negativa de Alyattes a entregar a sus suplicantes cuando Cyaxares envió a reclamarlos, estalló la guerra entre los lidios y los medos, y continuó durante cinco años, con varios éxitos. En el transcurso de él, los medos obtuvieron muchas victorias sobre los lidios, y los lidios también obtuvieron muchas victorias sobre los medos. Entre sus otras batallas hubo un compromiso nocturno. Sin embargo, como la balanza no se había inclinado a favor de ninguna de las dos naciones, tuvo lugar otro combate en el sexto año, en el curso del cual, cuando la batalla se estaba calentando, el día se convirtió de repente en noche. Este acontecimiento había sido predicho por Tales, el milesio, quien lo advirtió a los jonios, fijándole el año mismo en que realmente tuvo lugar. Los medos y lidios, cuando notaron el cambio, cesaron de pelear,
Sin embargo, según la lista de reyes medos y la duración de su reinado informada en otra parte por Heródoto, Cyaxares murió 10 años antes del eclipse.
Sagacidad
Diógenes Laërtius nos dice que los Siete Sabios fueron creados en el arconte de Damasio en Atenas alrededor del 582 a. C. y que Tales fue el primer sabio. La misma historia, sin embargo, afirma que Tales emigró a Mileto. También hay un informe de que no se convirtió en un estudioso de la naturaleza hasta después de su carrera política. Por mucho que nos gustaría tener una fecha sobre los siete sabios, debemos rechazar estas historias y la tentadora fecha si queremos creer que Tales era un nativo de Mileto, predijo el eclipse y estuvo con Creso en la campaña contra Ciro.
Tales recibió instrucción de un sacerdote egipcio y se dice que tuvo estrechos contactos con los sacerdotes de Tebas y su geometría lineal.
Era bastante seguro que provenía de una familia acomodada y establecida, en una clase que habitualmente proporcionaba educación superior a sus hijos. Además, el ciudadano corriente, a menos que fuera un marinero o un comerciante, no podía permitirse el gran viaje por Egipto y no se juntaba con nobles legisladores como Solón.
En el capítulo 1.39 de Vidas de filósofos eminentes de Diogenes Laërtius, Laërtius relata varias historias de un objeto costoso que debe ir a los más sabios. En una versión (que Laërtius atribuye a Callimachus en sus Iambics ), Bathycles de Arcadia declara en su testamento que un cuenco caro "se le debe dar a quien haya hecho el mayor bien con su sabiduría". Así que se lo dio a Tales, pasó la ronda de todos los sabios, y volvió a Tales de nuevo. Y se lo envió a Apolo en Dídima, con esta dedicatoria... "Tales el Milesio, hijo de Examyas [dedica esto] a Delphinian Apollo después de ganar dos veces el premio de todos los griegos.'"
Teorías
Los primeros griegos, y otras civilizaciones antes que ellos, a menudo invocaban explicaciones idiosincrásicas de los fenómenos naturales con referencia a la voluntad de dioses y héroes antropomórficos. En cambio, Thales pretendía explicar los fenómenos naturales a través de hipótesis racionales que hacían referencia a los propios procesos naturales. Por ejemplo, en lugar de asumir que los terremotos eran el resultado de caprichos sobrenaturales, Tales los explicó con la hipótesis de que la Tierra flota sobre el agua y que los terremotos ocurren cuando las olas sacuden la Tierra.
Tales era un hilozoísta (uno que piensa que la materia está viva, es decir, que contiene alma(s). Aristóteles escribió ( De Anima 411 a7-8) de Tales:... Tales pensó que todas las cosas están llenas de dioses. Aristóteles postula el origen de Tales pensó en la materia que generalmente contenía almas, pensando inicialmente en el hecho de que, debido a que los imanes mueven el hierro, la presencia de movimiento de la materia indicaba que esta materia contenía vida.
Tales, según Aristóteles, preguntó cuál era la naturaleza (griego arche ) del objeto para que se comportara de su forma característica. Physis ( φύσις ) proviene de phyein ( φύειν ), "crecer", relacionado con nuestra palabra "ser". (G)natura es la forma en que una cosa "nace", nuevamente con el sello de lo que es en sí misma.
Aristóteles caracteriza a la mayoría de los filósofos "al principio" ( πρῶτον ) pensando que los "principios en forma de materia eran los únicos principios de todas las cosas", donde "principio" es arche, "materia" es hyle ("madera" o "materia", "material") y "forma" es eidos.
Arche se traduce como "principio", pero las dos palabras no tienen exactamente el mismo significado. Un principio de algo es simplemente anterior (relacionado con pro-) a él, ya sea cronológica o lógicamente. Un arche (de ἄρχειν, "gobernar") domina un objeto de alguna manera. Si se toma el arché como un origen, entonces se implica una causalidad específica; es decir, se supone que B es característicamente B simplemente porque proviene de A, que lo domina.
Los archai que Aristóteles tenía en mente en su conocido pasaje sobre los primeros científicos griegos no son necesariamente cronológicamente anteriores a sus objetos, sino constituyentes de ellos. Por ejemplo, en el pluralismo los objetos están compuestos por tierra, aire, fuego y agua, pero esos elementos no desaparecen con la producción del objeto. Permanecen como archai dentro de él, al igual que los átomos de los atomistas.
Lo que Aristóteles realmente está diciendo es que los primeros filósofos estaban tratando de definir la(s) sustancia(s) de la(s) que están compuestos todos los objetos materiales. De hecho, eso es exactamente lo que los científicos modernos están tratando de lograr en física nuclear, que es una segunda razón por la que se describe a Tales como el primer científico occidental, pero algunos estudiosos contemporáneos rechazan esta interpretación.
Geometría
Thales era conocido por su uso innovador de la geometría y, a menudo, se lo considera la primera persona en el mundo occidental que aplicó el razonamiento deductivo a la geometría (y, por extensión, a menudo se lo considera el primer matemático occidental). Su comprensión era tanto teórica como práctica. Por ejemplo, dijo:
Megiston topos: apanta gar chorei ( Μέγιστον τόπος· ἄπαντα γὰρ χωρεῖ. )
El más grande es el espacio, porque contiene todas las cosas.
Topos está en el espacio de estilo newtoniano, ya que el verbo chorei tiene la connotación de ceder ante las cosas, o extenderse para dejarles espacio, lo cual es extensión. Dentro de esta extensión, las cosas tienen una posición. Puntos, líneas, planos y sólidos relacionados por distancias y ángulos se siguen de esta presunción.
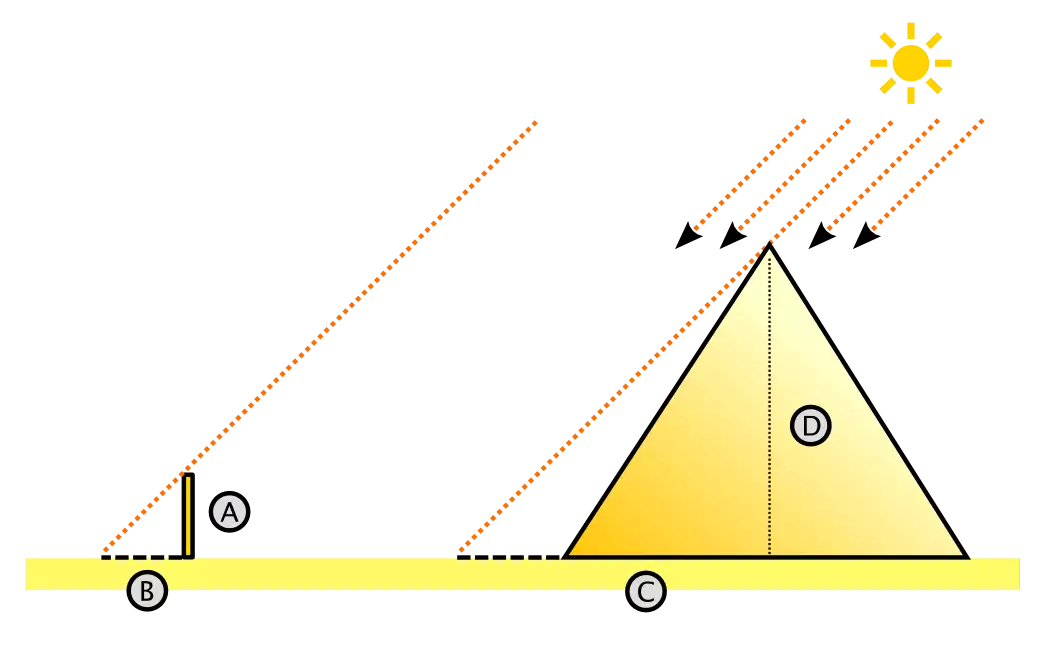
Tales entendió triángulos semejantes y triángulos rectángulos, y lo que es más, usó ese conocimiento de manera práctica. La historia se cuenta en Diógenes Laërtius (loc. cit.) que midió la altura de las pirámides por sus sombras en el momento en que su propia sombra era igual a su altura. Un triángulo rectángulo con dos catetos iguales es un triángulo rectángulo de 45 grados, todos los cuales son similares. La longitud de la sombra de la pirámide medida desde el centro de la pirámide en ese momento debe haber sido igual a su altura.
Esta historia indica que estaba familiarizado con el seked egipcio, o seqed, la relación entre la carrera y la elevación de una pendiente (cotangente). El seked está en la base de los problemas 56, 57, 58, 59 y 60 del papiro Rhind, un documento matemático del antiguo Egipto.
De manera más práctica, Tales usó el mismo método para medir las distancias de los barcos en el mar, dijo Eudemo según lo informado por Proclo ("en Euclidem"). Según Kirk & Raven, todo lo que necesitas para esta hazaña son tres palos rectos clavados en un extremo y el conocimiento de tu altitud. Un palo se clava verticalmente en el suelo. Se nivela un segundo. Con el tercero avistas el barco y calculas el seked a partir de la altura del palo y su distancia desde el punto de inserción hasta la línea de mira (Proclus, In Euclidem, 352).
Teoremas de Tales
Hay dos teoremas de Thales en geometría elemental, uno conocido como teorema de Thales que tiene que ver con un triángulo inscrito en un círculo y que tiene el diámetro del círculo como un cateto, el otro teorema también se llama teorema del intercepto. Además, Eudemo le atribuyó el descubrimiento de que un círculo es bisecado por su diámetro, que los ángulos de la base de un triángulo isósceles son iguales y que los ángulos verticales son iguales. Según una Nota histórica, cuando Tales visitó Egipto,observó que cada vez que los egipcios dibujaban dos líneas que se cruzaban, medían los ángulos verticales para asegurarse de que fueran iguales. Tales concluyó que se podría probar que todos los ángulos verticales son iguales si se aceptaran algunas nociones generales como: todos los ángulos rectos son iguales, los iguales sumados a iguales son iguales y los iguales restados de iguales son iguales.
La evidencia de la primacía de Tales nos llega de un libro de Proclo, quien escribió mil años después de Tales, pero se cree que tuvo una copia del libro de Eudemo. Proclus escribió: "Thales fue el primero en ir a Egipto y traer de regreso a Grecia este estudio". Continúa diciéndonos que además de aplicar los conocimientos adquiridos en Egipto "Él mismo descubrió muchas proposiciones y reveló los principios subyacentes de muchas otras a sus sucesores, siendo en algunos casos su método más general, en otros más empírico".
Otras citas de Proclus enumeran más logros matemáticos de Thales:
Dicen que Tales fue el primero en demostrar que el círculo es bisecado por el diámetro, siendo la causa de la bisección el paso sin obstáculos de la línea recta por el centro.
Se dice que [Thales] fue el primero en saber y en haber enunciado [el teorema] de que los ángulos en la base de cualquier triángulo isósceles son iguales, aunque de la manera más arcaica describió los ángulos iguales como similares.
Este teorema, que cuando dos líneas rectas se cortan entre sí, los ángulos verticales y opuestos son iguales, fue descubierto por primera vez, como dice Eudemo, por Tales, aunque la demostración científica fue mejorada por el escritor de Elementos.
Eudemo en su Historia de la Geometría atribuye este teorema [la igualdad de los triángulos que tienen dos ángulos y un lado igual] a Tales. Porque dice que el método por el cual Tales mostró cómo encontrar la distancia de los barcos en el mar implica necesariamente este método.
Pánfila dice que, habiendo aprendido geometría de los egipcios, él [Tales] fue el primero en inscribir en un círculo un triángulo rectángulo, tras lo cual sacrificó un buey.
Además de Proclo, Jerónimo de Rodas también cita a Tales como el primer matemático griego. Hieronymus sostuvo que Thales pudo medir la altura de las pirámides usando un teorema de geometría ahora conocido como el teorema de la intersección (después de recopilar datos usando su bastón y comparando su sombra con la proyectada por las pirámides). Recibimos variaciones de la historia de Hieronymus a través de Diógenes Laërtius, Plinio el Viejo y Plutarco. Según Hieronymus, citado históricamente por Diógenes Laërtius, Tales encontró la altura de las pirámides comparando las longitudes de las sombras proyectadas por una persona y por las pirámides.
Debido a las variaciones entre los testimonios, como la "historia del sacrificio de un buey con motivo del descubrimiento de que el ángulo sobre un diámetro de un círculo es un ángulo recto" en la versión contada por Diógenes Laërtius siendo acreditado a Pitágoras más bien que Thales, algunos historiadores (como DR Dicks) cuestionan si tales anécdotas tienen algún valor histórico.
El agua como primer principio
Aquello de lo que es todo lo que existe y de lo que primero se convierte y en lo que finalmente se convierte, quedando su sustancia debajo de él, pero transformándose en cualidades, que dicen que es el elemento y principio de las cosas que son... Porque es necesario que haya alguna naturaleza ( φύσις ), ya sea una o más de una, de la cual se vuelven las otras cosas del objeto que se salva... Tales, el fundador de este tipo de filosofía, dice que es el agua.
La posición filosófica más famosa de Tales fue su tesis cosmológica, que nos llega a través de un pasaje de la Metafísica de Aristóteles. En el trabajo, Aristóteles informó inequívocamente la hipótesis de Tales sobre la naturaleza de toda la materia: que el principio originario de la naturaleza era una sola sustancia material: el agua. Luego, Aristóteles procedió a ofrecer una serie de conjeturas basadas en sus propias observaciones para dar cierta credibilidad a por qué Tales pudo haber propuesto esta idea (aunque Aristóteles no la sostuvo).
Aristóteles expuso su propio pensamiento sobre la materia y la forma que puede arrojar algo de luz sobre las ideas de Tales, en Metafísica 983 b6 8–11, 17–21. (El pasaje contiene palabras que luego fueron adoptadas por la ciencia con significados bastante diferentes).
En esta cita vemos la descripción de Aristóteles del problema del cambio y la definición de sustancia. Preguntó si un objeto cambia, ¿es igual o diferente? En cualquier caso, ¿cómo puede haber un cambio de uno a otro? La respuesta es que la sustancia "se guarda", pero adquiere o pierde diferentes cualidades ( πάθη, las cosas que "experimentas").
Aristóteles conjeturó que Tales llegó a su conclusión al contemplar que "el alimento de todas las cosas es húmedo y que incluso lo caliente se crea a partir de lo húmedo y vive de él". Si bien la conjetura de Aristóteles sobre por qué Tales sostuvo el agua como el principio originario de la materia es su propio pensamiento, su afirmación de que Tales la consideró como agua se acepta generalmente como un origen genuino de Tales y se lo ve como un materialista incipiente.
Tales pensó que la Tierra debe ser un disco plano que flota en una extensión de agua.
Heráclito Homerico afirma que Tales sacó su conclusión al ver que la sustancia húmeda se convertía en aire, limo y tierra. Parece probable que Tales considerara que la Tierra se solidificaba a partir del agua sobre la que flotaba y los océanos que la rodeaban.
Escribiendo siglos después, Diógenes Laërtius también afirma que Tales enseñó que "el agua constituía ( ὑπεστήσατο, 'estaba debajo') el principio de todas las cosas".
Aristóteles consideró que la posición de Tales era más o menos equivalente a las ideas posteriores de Anaxímenes, quien sostenía que todo estaba compuesto de aire. El libro de 1870 Diccionario de biografía y mitología griega y romana señaló:
En su dogma de que el agua es el origen de las cosas, es decir, que es aquello de lo que surge todo y en lo que todo se resuelve, Tales pudo haber seguido cosmogonías órficas, mientras que, a diferencia de ellas, buscó establecer el verdad de la afirmación. Por lo tanto, Aristóteles, inmediatamente después de haberlo llamado el creador de la filosofía, presenta las razones que se creía que Tales había aducido en confirmación de esa afirmación; porque no existió ningún desarrollo escrito de él, o de hecho ningún libro de Tales, lo prueban las expresiones que usa Aristóteles cuando presenta las doctrinas y pruebas del milesio. (pág. 1016)
Creencias en la divinidad
Según Aristóteles, Tales pensaba que las piedras imanes tenían alma, porque el hierro se siente atraído por ellas (por la fuerza del magnetismo).
Aristóteles definió el alma como el principio de vida, aquello que impregna la materia y la hace vivir, dándole la animación o poder para actuar. La idea no se originó con él, ya que los griegos en general creían en la distinción entre mente y materia, lo que finalmente conduciría a una distinción no solo entre cuerpo y alma, sino también entre materia y energía. Si las cosas estuvieran vivas, deben tener almas. Esta creencia no fue una innovación, ya que las antiguas poblaciones ordinarias del Mediterráneo creían que las acciones naturales eran causadas por divinidades. En consecuencia, Aristóteles y otros escritores antiguos afirman que Tales creía que "todas las cosas estaban llenas de dioses". En su celo por convertirlo en el primero en todo, algunos dijeron que fue el primero en sostener la creencia, que debe haber sido ampliamente conocida como falsa.Sin embargo, Tales buscaba algo más general, una sustancia mental universal. Eso también estaba en el politeísmo de la época. Zeus era la personificación misma de la mente suprema, dominando todas las manifestaciones subordinadas. A partir de Tales, sin embargo, los filósofos tendieron a despersonificar u objetivar la mente, como si fuera la sustancia de la animación per se y no un dios como los otros dioses. El resultado fue una eliminación total de la mente de la sustancia, abriendo la puerta a un principio de acción no divino.
El pensamiento clásico, sin embargo, sólo había avanzado un poco por ese camino. En lugar de referirse a la persona, Zeus, hablaron de la gran mente:
"Thales", dice Cicerón, "asegura que el agua es el principio de todas las cosas, y que Dios es esa Mente que formó y creó todas las cosas a partir del agua".
La mente universal también aparece como una creencia romana en Virgilio:
Al principio, el ESPÍRITU interior (spiritus intus) fortalece el Cielo y la Tierra,
los campos acuáticos y el globo lúcido de la Luna, y luego – las
estrellas de Titán; y la mente (mens) infundida a través de los miembros
agita toda la masa y se mezcla con la GRAN MATERIA (magno corpore)
Según Henry Fielding (1775), Diógenes Laërtius (1.35) afirmó que Tales planteaba "la preexistencia independiente de Dios desde toda la eternidad, afirmando" que Dios era el más antiguo de todos los seres, pues existía sin causa previa incluso en el forma de generación; que el mundo era la más bella de todas las cosas; porque fue creado por Dios".
Influencias
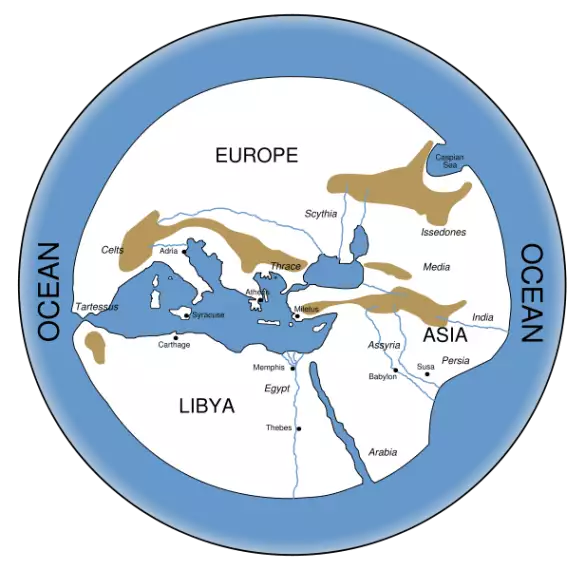
Debido a la escasez de fuentes sobre Tales y las discrepancias entre los relatos de las fuentes que han sobrevivido, existe un debate académico sobre las posibles influencias en Tales y los matemáticos griegos que lo sucedieron. El historiador Roger L. Cooke señala que Proclo no menciona la influencia mesopotámica en Tales o la geometría griega, pero "se muestra claramente en la astronomía griega, en el uso del sistema sexagesimal de medir ángulos y en el uso explícito de Ptolomeo de las observaciones astronómicas mesopotámicas".." Cooke señala que posiblemente también aparezca en el segundo libro de los Elementos de Euclides, "que contiene construcciones geométricas equivalentes a ciertas relaciones algebraicas que se encuentran con frecuencia en las tablillas cuneiformes". Cooke señala "Esta relación, sin embargo,
El historiador BL Van der Waerden se encuentra entre los que defienden la idea de la influencia mesopotámica y escribe: "Se deduce que tenemos que abandonar la creencia tradicional de que los matemáticos griegos más antiguos descubrieron la geometría completamente por sí mismos... una creencia que solo era sostenible mientras nada se sabía de las matemáticas babilónicas, lo cual no disminuye en modo alguno la estatura de Tales, al contrario, su genio sólo recibe ahora el honor que le corresponde, el honor de haber desarrollado una estructura lógica para la geometría, de haber introducido la prueba en la geometría.."
Algunos historiadores, como DR Dicks, no están de acuerdo con la idea de que podemos determinar a partir de las fuentes cuestionables que tenemos, cuán influenciado estaba Tales por las fuentes babilónicas. Señala que si bien se sostiene que Thales pudo calcular un eclipse usando un ciclo llamado "Saros" que se consideró "prestado de los babilonios", "los babilonios, sin embargo, no usaron ciclos para predecir eclipses solares, pero los calculó a partir de observaciones de la latitud de la luna hechas poco antes de la sicigia esperada".Dicks cita al historiador O. Neugebauer, quien relata que "No existía ninguna teoría babilónica para predecir el eclipse solar en el 600 a. C., como se puede ver en la situación muy insatisfactoria 400 años después; ni los babilonios desarrollaron ninguna teoría que tomara la influencia de la latitud geográfica. en cuenta." Dicks examina el ciclo denominado 'Saros', que se cree que usó Tales y que se cree que proviene de los babilonios. Señala que Ptolomeo hace uso de este y otro ciclo en su libro Mathematical Syntaxis pero lo atribuye a los astrónomos griegos anteriores a Hiparco y no a los babilonios.Dicks señala que Heródoto relata que Tales hizo uso de un ciclo para predecir el eclipse, pero sostiene que "si es así, el cumplimiento de la 'predicción' fue un golpe de pura suerte, no de ciencia". Va más allá uniéndose a otros historiadores (F. Martini, JLE Dreyer, O. Neugebauer) al rechazar por completo la historicidad de la historia del eclipse. Dicks vincula la historia de Tales descubriendo la causa de un eclipse solar con la afirmación de Heródoto de que Tales descubrió el ciclo del sol en relación con los solsticios, y concluye que "no es posible que haya poseído este conocimiento que ni los egipcios ni los babilonios ni sus sucesores inmediatos poseyeron". Josefo es el único historiador antiguo que afirma que Tales visitó Babilonia.
Herodoto escribió que los griegos aprendieron la práctica de dividir el día en 12 partes, sobre los polos y el gnomon de los babilonios. (Se desconoce el significado exacto de su uso de la palabra polos, las teorías actuales incluyen: "la cúpula celestial", "la punta del eje de la esfera celestial", o un reloj de sol esférico cóncavo). Sin embargo, incluso las afirmaciones de Herodoto sobre Babilonia influencia son cuestionados por algunos historiadores modernos, como L. Zhmud, quien señala que la división del día en doce partes (y por analogía el año) era conocida por los egipcios ya en el segundo milenio, el gnomon era conocido por ambos egipcios y babilonios, y la idea de la "esfera celestial" no se usaba fuera de Grecia en este momento.
Menos controvertida que la posición de que Tales aprendió las matemáticas babilónicas es la afirmación de que fue influenciado por los egipcios. Deliberadamente, el historiador SN Bychkov sostiene que la idea de que los ángulos de la base de un triángulo isósceles son iguales probablemente provino de Egipto. Esto se debe a que, al construir un techo para una casa, tener una sección transversal que sea exactamente un triángulo isósceles no es crucial (ya que es la cumbrera del techo la que debe encajar con precisión), en contraste, una pirámide cuadrada simétrica no puede tener errores en el ángulos base de las caras o no encajarán bien. El historiador DR Dicks está de acuerdo en que, en comparación con los griegos en la era de Tales, había un estado más avanzado de las matemáticas entre los babilonios y especialmente entre los egipcios: "ambas culturas conocían las fórmulas correctas para determinar las áreas y los volúmenes de figuras geométricas simples como triángulos, rectángulos, trapecios, etc.; los egipcios también podían calcular correctamente el volumen del tronco de una pirámide de base cuadrada (los babilonios usaban una fórmula incorrecta para esto), y usaban una fórmula para el área de un círculo..que da un valor para π de 3.1605, una buena aproximación". Dicks también está de acuerdo en que esto habría tenido un efecto en Tales (quien, según las fuentes más antiguas, estaba interesado en las matemáticas y la astronomía), pero sostiene que los relatos de los viajes de Tales por estas tierras son puro mito.
La antigua civilización y los enormes monumentos de Egipto tuvieron "una profunda e imborrable impresión en los griegos". Atribuían a los egipcios "un conocimiento inmemorial de ciertos temas" (incluida la geometría) y reclamaban el origen egipcio de algunas de sus propias ideas para tratar de prestarles "una antigüedad respetable" (como la literatura "hermética" del período alejandrino).
Dicks sostiene que, dado que Tales era una figura prominente en la historia griega en la época de Eudemo, "no se sabía nada seguro excepto que vivía en Mileto". Se desarrolló una tradición de que, como "los milesios estaban en condiciones de poder viajar mucho", Tales debe haber ido a Egipto. Como Heródoto dice que Egipto fue el lugar de nacimiento de la geometría, debe haberlo aprendido mientras estuvo allí. Como tenía que haber estado allí, seguramente una de las teorías sobre las inundaciones del Nilo expuestas por Herodoto debe haber venido de Tales. Del mismo modo, como debe haber estado en Egipto, tuvo que haber hecho algo con las pirámides, de ahí la historia de medirlas. Existen historias apócrifas similares de Pitágoras y Platón viajando a Egipto sin evidencia que lo corrobore.
Como la geometría egipcia y babilónica en ese momento era "esencialmente aritmética", usaron números reales y "luego se describe el procedimiento con instrucciones explícitas sobre qué hacer con estos números", no se mencionó cómo se hicieron las reglas de procedimiento., y nada hacia un corpus ordenado lógicamente de conocimiento geométrico generalizado con 'pruebas' analíticas como las que encontramos en las palabras de Euclides, Arquímedes y Apolonio”. se cree que retomó allí (especialmente porque no hay evidencia de que los griegos de esta época pudieran usar jeroglíficos egipcios).
Asimismo, hasta alrededor del siglo II a. C. y la época de Hiparco (c. 190-120 a. C.), se desconocía la división general babilónica del círculo en 360 grados y su sistema sexagesimal. Heródoto no dice casi nada sobre la literatura y la ciencia babilónicas, y muy poco sobre su historia. Algunos historiadores, como P. Schnabel, sostienen que los griegos solo aprendieron más sobre la cultura babilónica de Berossus, un sacerdote babilónico del que se dice que estableció una escuela en Cos alrededor del 270 a. C. (pero hasta qué punto esto tuvo en el campo de la geometría es impugnado).
Dicks señala que el estado primitivo de las matemáticas griegas y las ideas astronómicas exhibidas por las nociones peculiares de los sucesores de Tales (como Anaximandro, Anaxímenes, Jenófanes y Heráclito), que el historiador JL Heiberg llama "una mezcla de intuición brillante y analogías infantiles"., argumenta en contra de las afirmaciones de los escritores de la antigüedad tardía de que Tales descubrió y enseñó conceptos avanzados en estos campos.
John Burnet (1892) señaló
Por último, tenemos un caso admitido de un gremio filosófico, el de los pitagóricos. Y se encontrará que la hipótesis, si ha de llamarse con ese nombre, de una organización regular de la actividad científica explicará por sí sola todos los hechos. El desarrollo de la doctrina de la mano de Tales, Anaximandro y Anaxímenes, por ejemplo, sólo puede entenderse como la elaboración de una sola idea en una escuela de tradición continua.
Según la enciclopedia bizantina Suda del siglo X, Tales había sido el "maestro y pariente" de Anaximandro.
Nicholas Molinari ha defendido recientemente una importante influencia griega en la idea de Archai de Tales, a saber, la deidad arcaica del agua Acheloios, que fue equiparada con el agua y adorada en Mileto durante la vida de Tales. Argumenta que Tales, como sabio y viajero del mundo, estuvo expuesto a muchas mitologías y religiones, y aunque todas tuvieron alguna influencia, su ciudad natal, Acheloios, fue la más esencial. Como evidencia, señala el hecho de que hydor significaba específicamente "agua dulce", y que Acheloios era visto como un cambiaformas en el mito y el arte, tan capaz de convertirse en cualquier cosa. También señala que los ríos del mundo eran vistos como los "tendones de Acheloios" en la antigüedad, y esta multiplicidad de deidades se refleja en la idea de Tales de que "
Interpretaciones
En la larga estancia de la filosofía, apenas ha existido un filósofo o historiador de la filosofía que no mencionara a Tales y tratara de caracterizarlo de alguna manera. Generalmente se le reconoce por haber aportado algo nuevo al pensamiento humano. Ya existían las matemáticas, la astronomía y la medicina. Tales agregó algo a estas diferentes colecciones de conocimiento para producir una universalidad que, hasta donde nos dice la escritura, no estaba en la tradición antes, pero resultó en un nuevo campo.
Desde entonces, las personas interesadas han estado preguntando qué es ese algo nuevo. Las respuestas se dividen en (al menos) dos categorías, la teoría y el método. Una vez que se ha llegado a una respuesta, el siguiente paso lógico es preguntar cómo Tales se compara con otros filósofos, lo que lleva a su clasificación (correcta o incorrecta).
Teoría
Los epítetos más naturales de Tales son "materialista" y "naturalista", que se basan en ousia y physis. La Enciclopedia Católica señala que Aristóteles lo llamó fisiólogo, con el significado de "estudiante de la naturaleza". Por otro lado, se habría calificado como uno de los primeros físicos, como lo hizo Aristóteles. Estudiaron corpora, "cuerpos", los descendientes medievales de las sustancias.
Russell
La mayoría está de acuerdo en que el sello de Tales en el pensamiento es la unidad de la sustancia, de ahí Bertrand Russell:
La opinión de que toda la materia es una es una hipótesis científica bastante respetable.... Pero sigue siendo una hermosa hazaña haber descubierto que una sustancia sigue siendo la misma en diferentes estados de agregación.
Russell solo reflejaba una tradición establecida; por ejemplo: Nietzsche, en su Filosofía en la Edad Trágica de los Griegos, escribió:
La filosofía griega parece comenzar con una noción absurda, con la proposición de que el agua es el origen primordial y la matriz de todas las cosas. ¿Es realmente necesario que tomemos en serio esta proposición? Lo es, y por tres razones. Primero, porque nos dice algo sobre el origen primigenio de todas las cosas; segundo, porque lo hace en un lenguaje desprovisto de imagen o fábula, y finalmente, porque contenido en él, aunque sea embrionariamente, es el pensamiento, "todas las cosas son una".
Este tipo de materialismo, sin embargo, no debe confundirse con el materialismo determinista. Tales sólo intentaba explicar la unidad observada en el libre juego de las cualidades. La llegada de la incertidumbre al mundo moderno hizo posible un regreso a Tales; por ejemplo, John Elof Boodin escribe ("Dios y la creación"):
No podemos leer el universo desde el pasado...
Boodin
Boodin define un materialismo "emergente", en el que los objetos de los sentidos emergen inciertos del sustrato. Tales es el innovador de este tipo de materialismo.
Feldman
Los pensadores escolásticos posteriores mantendrían que en su elección del agua Tales estuvo influenciado por la religión babilónica o caldea, que sostenía que un dios había comenzado la creación actuando sobre el agua preexistente. El historiador Abraham Feldman sostiene que esto no se sostiene bajo un examen más detenido. En la religión babilónica el agua no tiene vida y es estéril hasta que un dios actúa sobre ella, pero para Tales el agua misma era divina y creativa. Sostenía que "Todas las cosas están llenas de dioses", y comprender la naturaleza de las cosas era descubrir los secretos de las deidades, y a través de este conocimiento abrir la posibilidad de que uno pudiera ser más grande que el más grandioso olímpico.
Feldman señala que, mientras que otros pensadores reconocieron la humedad del mundo, "ninguno de ellos se inspiró para concluir que, en última instancia, todo era acuático". Señala además que Tales era "un ciudadano acaudalado del fabulosamente rico puerto oriental de Mileto... comerciante en los productos básicos de la antigüedad, vino y aceite... Ciertamente manejaba los mariscos de los fenicios que secretaban el tinte de púrpura imperial".Feldman recuerda las historias de Tales midiendo la distancia de los barcos en el puerto, creando mejoras mecánicas para la navegación de los barcos, dando una explicación de la inundación del Nilo (vital para la agricultura egipcia y el comercio griego), y cambiando el curso del río Halys para que un ejército podría vadearlo. En lugar de ver el agua como una barrera, Tales contempló la reunión religiosa anual jónica para el ritual atlético (que se celebra en el promontorio de Mycale y se cree que fue ordenada por la familia ancestral de Poseidón, el dios del mar). Pidió a los estados mercantiles jónicos que participaran en este ritual que lo convirtieran en una federación democrática bajo la protección de Poseidón que mantendría a raya a las fuerzas de la pastoral Persia. Feldman concluye que Tales vio "y "el canal común de los estados".
Feldman considera el entorno de Thales y sostiene que Thales habría visto las lágrimas, el sudor y la sangre como otorgando valor al trabajo de una persona y el medio por el cual viajaban las mercancías que dan vida (ya sea en cuerpos de agua o a través del sudor de esclavos y animales de carga). Habría visto que los minerales podrían procesarse a partir del agua, como la sal que sustenta la vida y el oro extraído de los ríos. Habría visto peces y otros alimentos recogidos de él. Feldman señala que Tales sostenía que la piedra imán estaba viva mientras atraía los metales hacia sí misma. Sostiene que Tales "viviendo siempre a la vista de su amado mar" vería que el agua parece atraer todo "el tráfico de vino y aceite, leche y miel, jugos y colorantes" hacia sí misma, llevándolo a "Feldman concluye que para Thales "... el agua unía todas las cosas. El significado social del agua en la época de Tales lo indujo a discernir a través del hardware y los productos secos, a través del suelo y el esperma, la sangre, el sudor y las lágrimas, una materia fluida fundamental... agua, el material más común y poderoso conocido por él". Esto, combinado con la idea de su contemporáneo de la "generación espontánea", nos permite ver cómo Tales podía sostener que el agua podía ser divina y creativa.
Feldman señala la asociación duradera de la teoría de que "todo lo que es humedad" con el propio Tales, y señala que Diógenes Laërtius habla de un poema, probablemente una sátira, donde el sol lleva a Tales al cielo.
Auge de la investigación teórica
En Occidente, Thales también representa un nuevo tipo de comunidad investigadora. Edmund Husserl intenta capturar el nuevo movimiento de la siguiente manera. El hombre filosófico es una "nueva configuración cultural" basada en alejarse de la "tradición preestablecida" y emprender una "indagación racional sobre lo que es verdadero en sí mismo"; es decir, un ideal de verdad. Comienza con individuos aislados como Thales, pero se les apoya y coopera con el paso del tiempo. Finalmente, el ideal transforma las normas de la sociedad, saltando las fronteras nacionales.
Clasificación
El término "presocrático" se deriva en última instancia del filósofo Aristóteles, quien distinguió a los primeros filósofos por preocuparse por la sustancia.
Diógenes Laërtius, por otro lado, adoptó un enfoque estrictamente geográfico y étnico. Los filósofos eran jónicos o italianos. Usó "jónico" en un sentido más amplio, incluidos también los académicos atenienses, que no eran presocráticos. Desde un punto de vista filosófico, cualquier agrupación habría sido igual de eficaz. No hay base para una unidad jónica o italiana. Sin embargo, algunos eruditos aceptan el esquema de Diógenes en cuanto a referirse a una escuela "jónica". No había tal escuela en ningún sentido.
El enfoque más popular se refiere a una escuela milesia, que es más justificable social y filosóficamente. Buscaron la sustancia de los fenómenos y pueden haber estudiado entre ellos. Algunos escritores antiguos los califican como Milesioi, "de Mileto".
Influencia en otros
Tales tuvo una profunda influencia en otros pensadores griegos y, por tanto, en la historia occidental. Algunos creen que Anaximandro fue alumno de Tales. Las primeras fuentes informan que uno de los alumnos más famosos de Anaximandro, Pitágoras, visitó a Tales cuando era joven y que Tales le aconsejó que viajara a Egipto para continuar sus estudios filosóficos y matemáticos.
Muchos filósofos siguieron el ejemplo de Tales al buscar explicaciones sobre la naturaleza en la naturaleza misma y no en lo sobrenatural, lo cual da inicio a una visión científica y empírica de la realidad tangible. Otros volvieron a las explicaciones sobrenaturales, pero las expresaron en el lenguaje de la filosofía en lugar del mito o la religión.
Mirando específicamente la influencia de Tales durante la era presocrática, es claro que se destacó como uno de los primeros pensadores que pensó más en el camino de los logos que en el de los mitos. La diferencia entre estas dos formas más profundas de ver el mundo es que el mito se concentra en torno a las historias de origen sagrado, mientras que el logos se concentra en la argumentación. Cuando el hombre mítico quiere explicar el mundo como él lo ve, lo explica a partir de dioses y poderes. El pensamiento mítico no diferencia entre cosas y personas y, además, no diferencia entre naturaleza y cultura. La forma en que un logotipo, El pensador presentaría una visión del mundo radicalmente distinta a la del pensador mítico. En su forma concreta, el logos es una forma de pensar no solo sobre el individualismo, sino también sobre lo abstracto. Además, se centra en la argumentación sensata y continua. Esto sienta las bases de la filosofía y su forma de explicar el mundo en términos de argumentación abstracta, y no a la manera de dioses e historias míticas.
Confiabilidad de las fuentes
Debido al elevado estatus de Tales en la cultura griega, un intenso interés y admiración siguieron a su reputación. Debido a este seguimiento, las historias orales sobre su vida estuvieron abiertas a la amplificación y la fabricación histórica, incluso antes de que fueran escritas generaciones después. La mayoría de las disensiones modernas provienen de tratar de interpretar lo que sabemos, en particular, distinguiendo la leyenda de los hechos.
Clasificación cronológica
El historiador DR Dicks y otros historiadores dividen las fuentes antiguas sobre Tales en las anteriores al 320 a. C. y las posteriores a ese año (algunas como Proclo escribiendo en el siglo V d. C. y Simplicio de Cilicia en el siglo VI d. C. escribiendo casi un milenio después de su era). La primera categoría incluye a Herodoto, Platón, Aristóteles, Aristófanes y Teofrasto, entre otros. La segunda categoría incluye a Plauto, Aecio, Eusebio, Plutarco, Josefo, Jámblico, Diógenes Laercio, Teón de Esmirna, Apuleyo, Clemente de Alejandría, Plinio el Viejo y Juan Tzetzes, entre otros.
Fuentes más antiguas
Las fuentes más antiguas sobre Tales (viviendo antes del 320 a. C.) son a menudo las mismas para los otros filósofos milesios (Anaximandro y Anaxímenes). Estas fuentes fueron más o menos contemporáneas (como Heródoto) o vivieron unos pocos cientos de años después de su fallecimiento. Además, escribían a partir de una tradición oral muy extendida y bien conocida en la Grecia de su época.
Últimas fuentes
Las últimas fuentes sobre Tales son varias "atribuciones de comentaristas y compiladores que vivieron entre 700 y 1000 años después de su muerte" que incluyen "anécdotas de diversos grados de plausibilidad" y, en opinión de algunos historiadores (como DR Dicks) de " sin valor histórico alguno". Dicks señala que no hay acuerdo "entre las 'autoridades' ni siquiera sobre los hechos más fundamentales de su vida, por ejemplo, si era milesio o fenicio, si dejó escritos o no, si estaba casado o soltero, mucho más". menos en las ideas reales y los logros con los que se le atribuye ".
Comparación de los dos grupos de fuentes
Al contrastar el trabajo de los escritores más antiguos con los de los últimos, Dicks señala que en los trabajos de los primeros escritores, Tales y los otros hombres que serían aclamados como "los Siete Sabios de Grecia" tenían una reputación diferente a la que tendrían. ser asignados a ellos por autores posteriores. Más cerca de su propia época, Tales, Solón, Bias de Priene, Pittacus de Mytilene y otros fueron aclamados como "hombres esencialmente prácticos que desempeñaron papeles de liderazgo en los asuntos de sus respectivos estados, y fueron mucho más conocidos por los primeros griegos como legisladores y legisladores". estadistas que como profundos pensadores y filósofos". Por ejemplo, Platón lo elogia (junto con Anacharsis) por ser el creador del torno de alfarero y el ancla.
Solo en los escritos del segundo grupo de escritores (que trabajaron después del 320 a. C.) "obtenemos la imagen de Tales como el pionero en el pensamiento científico griego, particularmente en relación con las matemáticas y la astronomía que se supone que aprendió en Babilonia y Egipto." En lugar de "la tradición anterior [donde] es un ejemplo favorito del hombre inteligente que posee algunos 'saber hacer' técnicos... los doxógrafos posteriores [como Dicearco en la segunda mitad del siglo IV a. C.] le imponen cualquier número de descubrimientos y logros, con el fin de construirlo como una figura de sabiduría sobrehumana".
Problema sugerido por Dicks
Dicks señala que surge un problema adicional en la información sobreviviente sobre Tales, ya que en lugar de usar fuentes antiguas más cercanas a la era de Tales, los autores en la antigüedad posterior ("epitomadores, extractores y compiladores" ) en realidad "prefirieron usar uno o más intermediarios, de modo que lo que realmente leemos en ellos nos llega ni siquiera de segunda, sino de tercera o cuarta o quinta mano. Obviamente, este uso de fuentes intermedias, copiadas y recopiadas de siglo en siglo, con cada escritor agregando piezas adicionales de información de mayor o menor verosimilitud de su propio conocimiento, proporcionó un campo fértil para errores en la transmisión, adscripciones erróneas y atribuciones ficticias".Dicks señala que "ciertas doctrinas que los comentaristas posteriores inventaron para Tales... fueron luego aceptadas en la tradición biográfica" siendo copiadas por escritores posteriores que luego fueron citados por los que vinieron después de ellos "y por lo tanto, debido a que pueden ser repetidas por diferentes autores basándose en diferentes fuentes, puede producir una impresión ilusoria de autenticidad".
Aristóteles
Incluso existen dudas al considerar las posiciones filosóficas que se sostiene que tienen su origen en Tales "en realidad estas se derivan directamente de las propias interpretaciones de Aristóteles que luego se incorporaron a la tradición doxográfica como adscripciones erróneas a Tales". (El mismo tratamiento fue dado por Aristóteles a Anaxágoras.)
La mayoría de los análisis filosóficos de la filosofía de Tales provienen de Aristóteles, un filósofo profesional, tutor de Alejandro Magno, quien escribió 200 años después de la muerte de Tales. Aristóteles, a juzgar por sus libros supervivientes, no parece tener acceso a ninguna obra de Tales, aunque probablemente tuvo acceso a obras de otros autores sobre Tales, como Heródoto, Hecateo, Platón, etc., así como a otros cuya obra es ahora extinto. El objetivo expreso de Aristóteles era presentar el trabajo de Tales no porque fuera significativo en sí mismo, sino como un preludio de su propio trabajo en filosofía natural.Geoffrey Kirk y John Raven, compiladores ingleses de los fragmentos de los presocráticos, afirman que los "juicios de Aristóteles a menudo están distorsionados por su visión de la filosofía anterior como un avance a tropezones hacia la verdad que el propio Aristóteles reveló en sus doctrinas físicas". También había una extensa tradición oral. Tanto el oral como el escrito eran comúnmente leídos o conocidos por todos los hombres educados de la región.
La filosofía de Aristóteles tenía un sello distintivo: profesaba la teoría de la materia y la forma, que los escolásticos modernos han denominado hilomorfismo. Aunque alguna vez estuvo muy extendido, no fue adoptado generalmente por la ciencia moderna y racionalista, ya que es útil principalmente en análisis metafísicos, pero no se presta a los detalles que son de interés para la ciencia moderna. No está claro si la teoría de la materia y la forma existió ya en Tales, y si existió, si Tales la abrazó.
Si bien algunos historiadores, como B. Snell, sostienen que Aristóteles se basaba en un registro escrito preplatónico de Hipias en lugar de la tradición oral, esta es una posición controvertida. En representación del consenso académico, Dicks afirma que "la tradición sobre él, incluso ya en el siglo V a. C., evidentemente se basaba por completo en rumores... Parecería que ya en la época de Aristóteles, los primeros jonios eran en gran parte nombres solo a los que la tradición popular. adjuntó varias ideas o realizaciones con mayor o menor plausibilidad".Señala que las obras que Anaximandro y Jenófanes confirmaron que existieron en el siglo VI a. C. ya habían desaparecido en el siglo IV a. C., por lo que las posibilidades de que el material presocrático sobreviva hasta la época de Aristóteles son casi nulas alumnos Teofrasto y Eudemo y menos probable aún para los que les siguen).
Diógenes Laercio
La principal fuente secundaria sobre los detalles de la vida y la carrera de Tales es Diógenes Laërtius, " Vidas de filósofos eminentes ". Esta es principalmente una obra biográfica, como su nombre lo indica. Comparado con Aristóteles, Diógenes no es un gran filósofo. Él es quien, en el Prólogo de esa obra, es responsable de la división de los primeros filósofos en "jónicos" e "italianos", pero ubica a los académicos en la escuela jónica y, por lo demás, evidencia un considerable desorden y contradicción, especialmente en la larga sección sobre los precursores de la "Escuela Jónica". Diógenes cita dos cartas atribuidas a Tales, pero Diógenes escribió unos ocho siglos después de la muerte de Tales y sus fuentes a menudo contenían "de ahí la preocupación por separar los hechos de la leyenda en los relatos de Tales.
Es debido a este uso de rumores y la falta de citar fuentes originales que lleva a algunos historiadores, como Dicks y Werner Jaeger, a mirar el origen tardío de la imagen tradicional de la filosofía presocrática y ver la idea completa como una construcción de una edad posterior, "el cuadro completo que nos ha llegado de la historia de la filosofía primitiva se formó durante las dos o tres generaciones desde Platón hasta los alumnos inmediatos de Aristóteles".
Contenido relacionado
Crates de Tebas
Rey filósofo
Posidonio