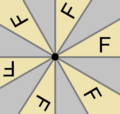
Simetría rotacional

La simetría rotacional, también conocida como simetría radial en geometría, es la propiedad que tiene una forma cuando se ve igual después de alguna rotación de un giro parcial. El grado de simetría rotacional de un objeto es el número de orientaciones distintas en las que se ve exactamente igual en cada rotación.

Ciertos objetos geométricos son parcialmente simétricos cuando se giran en ciertos ángulos, como cuadrados girados 90°; sin embargo, los únicos objetos geométricos que son completamente simétricos rotacionalmente en cualquier ángulo son las esferas, los círculos y otros esferoides.

Trato formal

Formalmente, la simetría rotacional es simetría con respecto a algunas o todas las rotaciones en el espacio euclidiano de m-dimensional. Las rotaciones son isometrías directas, es decir, isometrías que conservan la orientación. Por lo tanto, un grupo de simetría de simetría rotacional es un subgrupo de E ⁺(m) (ver grupo euclidiano).

La simetría con respecto a todas las rotaciones sobre todos los puntos implica simetría traslacional con respecto a todas las traslaciones, por lo que el espacio es homogéneo y el grupo de simetría es el conjunto E( m). Con la noción modificada de simetría para campos vectoriales, el grupo de simetría también puede ser E ⁺(m).

Para simetría con respecto a rotaciones alrededor de un punto, podemos tomar ese punto como origen. Estas rotaciones forman el grupo ortogonal especial SO(m), el grupo de m × m matrices ortogonales con determinante 1. Para m = 3 este es el grupo de rotación SO(3).

En otra definición de la palabra, el grupo de rotación de un objeto es el grupo de simetría dentro de E ⁺(n), el grupo de isometrías directas; en otras palabras, la intersección del grupo de simetría total y el grupo de isometrías directas. Para objetos quirales es lo mismo que el grupo de simetría completo.

Las leyes de la física son invariantes SO(3) si no distinguen diferentes direcciones en el espacio. Debido al teorema de Noether, la simetría rotacional de un sistema físico es equivalente a la ley de conservación del momento angular.

Simetría rotacional discreta

Simetría rotacional del orden n, también llamado n- simetría rotacional múltipleo simetría rotacional discreta de la nth order, con respecto a un punto particular (en 2D) o eje (en 3D) significa que la rotación por un ángulo de 360∘ ∘ n{displaystyle {tfrac {360^{cccfn\fnMicrosoft {fn\\fn\fn\\fn\\\\\fn\\\\\fn\\\fn\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ } {n}} (180°, 120°, 90°, 72°, 60°, 51 3.7°, etc.) no cambia el objeto. Una simetría "1 veces" no es simetría (todos los objetos parecen iguales después de una rotación de 360°).

La notación para la simetría n-fold es C_n o simplemente n. El grupo de simetría real se especifica mediante el punto o eje de simetría, junto con el n. Para cada punto o eje de simetría, el tipo de grupo abstracto es un grupo cíclico de orden n, Z_n. Aunque para este último también se utiliza la notación C_n, la geométrica y abstracta C_n debe distinguirse: hay otros grupos de simetría del mismo tipo de grupo abstracto que son geométricamente diferentes, ver cíclico Grupos de simetría en 3D.

El dominio fundamental es un sector de 360∘ ∘ n.{displaystyle {tfrac {360^{cccfn\fnMicrosoft {fn\\fn\fn\\fn\\\\\fn\\\\\fn\\\fn\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ - Sí.

Ejemplos sin simetría de reflexión adicional:

• n = 2, 180°: el dyad; letras Z, N, S; los contornos, aunque no los colores, del símbolo yin y yang; la bandera de la Unión (como dividida a lo largo de la diagonal de la bandera y girada sobre el punto central de la bandera)
• n = 3, 120°: triad, triskelion, anillos Borromean; a veces el término simetría trilateral se utiliza;
• n = 4, 90°: tetrad, swastika
• n = 6, 60°: hexad, Estrella de David (este tiene simetría de reflexión adicional)
• n = 8, 45°: octad, Muqarnas Octagonal, generadas por ordenador (CG), techo

C_n es el grupo de rotación de un polígono de ncaras en 2D y de n- pirámide de lados en 3D.

Si hay, p.e. simetría rotacional con respecto a un ángulo de 100°, luego también con respecto a uno de 20°, el máximo común divisor de 100° y 360°.

Un objeto 3D típico con simetría rotacional (posiblemente también con ejes perpendiculares) pero sin simetría especular es una hélice.

Ejemplos

C2 (más)	C3 (más)	C4 (más)	C5 (más)	C6 (más)
Doble péndulo fractal	Signo de tráfico de la rotonda		US Bicentennial Star
La posición inicial en shogi	Snoldelev Stone está entrelazado bebiendo cuernos diseño

Múltiples ejes de simetría que pasan por el mismo punto

Para simetría discreta con múltiples ejes de simetría que pasan por el mismo punto, existen las siguientes posibilidades:

• Además de un n- eje múltiple, n perpendicular 2 ejes: los grupos dihedral D_n de orden 2n ()n ≥ 2). Este es el grupo de rotación de un prisma regular, o bipyramid regular. Aunque se utiliza la misma notación, la geométrica y abstracta D_n debe distinguirse: hay otros grupos de simetría del mismo tipo de grupo abstracto que son geométricamente diferentes, ver grupos de simetría dihedral en 3D.
• ejes de 4×3 y 3×2: el grupo de rotación T de orden 12 de un tetraedro regular. El grupo es isomorfo al grupo alternante A₄.
• 3×4-fold, 4×3-fold, y 6×2-fold ejes: el grupo de rotación O de orden 24 de cubo y un octaedro regular. El grupo es isomorfo al grupo simétrico S₄.
• 6×5-fold, 10×3-fold, y 15×2-fold ejes: el grupo de rotación I of order 60 of a dodecahedron and an icosahedron. El grupo es isomorfo al grupo alternante A₅. El grupo contiene 10 versiones de D₃ y 6 versiones de D₅ (simetrías rotacionales como prismas y antiprismos).

En el caso de los sólidos platónicos, los ejes dobles pasan por los puntos medios de las aristas opuestas, y el número de ellos es la mitad del número de aristas. Los otros ejes pasan por vértices opuestos y por centros de caras opuestas, excepto en el caso del tetraedro, donde los tres ejes pasan cada uno por un vértice y el centro de una cara.

Simetría rotacional con respecto a cualquier ángulo

La simetría rotacional con respecto a cualquier ángulo es, en dos dimensiones, simetría circular. El dominio fundamental es una media línea.

En tres dimensiones podemos distinguir simetría cilíndrica y simetría esférica (sin cambios al girar sobre un eje, ni para cualquier rotación). Es decir, no hay dependencia del ángulo usando coordenadas cilíndricas ni dependencia de ninguno de los ángulos usando coordenadas esféricas. El dominio fundamental es un semiplano que pasa por el eje y una semilínea radial, respectivamente. Axisimétrico y axisimétrico son adjetivos que se refieren a un objeto que tiene simetría cilíndrica, o axisimetría (es decir, simetría rotacional con respecto a un eje central) como un rosquilla (toro). Un ejemplo de simetría esférica aproximada es la Tierra (con respecto a la densidad y otras propiedades físicas y químicas).

En 4D, la simetría rotacional continua o discreta alrededor de un plano corresponde a la simetría rotacional 2D correspondiente en cada plano perpendicular, alrededor del punto de intersección. Un objeto también puede tener simetría rotacional con respecto a dos planos perpendiculares, p. si es el producto cartesiano de dos figuras 2D con simetría rotacional, como en el caso de, p. el duocilindro y varios duoprismas regulares.

Simetría rotacional con simetría traslacional

Arreglo dentro de una célula primitiva de rotocentros 2 y 4 veces. Un dominio fundamental se indica en amarillo.

Arreglo dentro de una célula primitiva de rotocentros 2, 3 y 6 veces, solo o en combinación (considerar el símbolo 6 veces como una combinación de un símbolo 2 y 3 veces); en el caso de la simetría 2 veces, la forma del paralelograma puede ser diferente. Para el caso p6, un dominio fundamental se indica en amarillo.

La simetría rotacional doble junto con la simetría traslacional simple es uno de los grupos Frieze. Un rotocentro es el punto fijo o invariante de una rotación. Hay dos rotocentros por celda primitiva.

Junto con la doble simetría traslacional, los grupos de rotación son los siguientes grupos de papel tapiz, con ejes por celda primitiva:

• p2 (2222): 4×2-fold; grupo de rotación de una celosía paralela, rectangular y rhombic.
• p3 (333): 3×3 veces; no el grupo de rotación de cualquier rejilla (cada rejilla está al revés de la misma, pero que no se aplica para esta simetría); es, por ejemplo, el grupo de rotación del revestimiento triangular regular con los triángulos equiláteros de colores alternadamente.
• p4 (442): 2×4-fold, 2×2-fold; grupo de rotación de una celosía cuadrada.
• p6 (632): 1×6-fold, 2×3-fold, 3×2-fold; grupo de rotación de una celosía hexagonal.
• Los rotocentros dobles (incluidos 4 veces y 6 veces), si están presentes en absoluto, forman el trazado de una rejilla igual a la rejilla traduccional, escalada por un factor 1/2. En el caso de la simetría traduccional en una dimensión, una propiedad similar se aplica, aunque el término "lattice" no se aplica.
• 3 rotocentros (incluidos 6 veces), si están presentes en absoluto, forman una rejilla hexagonal regular igual a la rejilla traduccional, rota por 30° (o equivalente a 90°) y escalada por un factor 133{displaystyle {tfrac {}{3}{sqrt {3}} {}} {fn}} {fn}}} {fn}}} {fn}}}}} {fn}}}}}}}}} {f}}}}}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {
• 4 rotocentros, si están presentes en absoluto, forman una rejilla cuadrada regular igual a la rejilla traduccional, rotada por 45°, y escalada por un factor 122{fnMicroc} {fnK}} {fn}}} {fn}} {fn}} {fn}} {fn}}}} {fn}}}} {fn}}}}}}}}}}}} {f}}}}}}} {fn}}}}}}}}}}}}} {
• Los rotocentros de 6 veces, si están presentes en absoluto, forman una celosa hexagonal regular que es el resultado de la celosía traduccional.

El escalado de una celosía divide el número de puntos por área unitaria por el cuadrado del factor de escala. Por lo tanto, el número de rotocentros 2-, 3-, 4- y 6-fold por célula primitiva es 4, 3, 2, y 1, respectivamente, incluyendo de nuevo 4-fold como un caso especial de 2-fold, etc.

Simetría rotacional 3 veces en un punto y 2 veces en otro (o ditto en 3D con respecto a ejes paralelos) implica grupo de rotación p6, es decir, simetría doble traduccional y simetría rotacional 6 veces en algún punto (o, en 3D, eje paralelo). La distancia de traducción para la simetría generada por un tal par de rotocentros es 23{displaystyle 2{sqrt {3}} veces su distancia.

Avión de Euclide	Avión hiperbólico
Tiling triangular Hexakis, un ejemplo de p6, [6,3]+, (632) (con colores) y p6m, [6,3], (*632) (sin colores); las líneas son ejes de reflexión si se ignoran los colores, y un tipo especial de eje de simetría si no se ignoran los colores: la reflexión revierte los colores. Se pueden distinguir rejillas de línea rectangular en tres orientaciones.	Orden 3-7 kisrhombille, un ejemplo de [7,3]+ (732) simetría y [7,3], (*732) (sin colores)