Probabilidad a priori

Compartir Imprimir Citar
Probabilidad a priori en el Teorema de Bayes

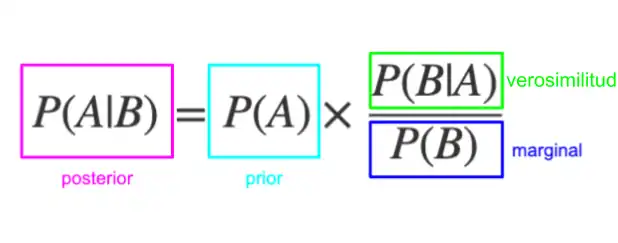
La probabilidad a priori o previa, es una estimación de la probabilidad de que ocurra un evento antes de observarlo o de tener en cuenta cualquier nueva evidencia. Esta suposición inicial tiene diferentes niveles de verosimilitud y ofrece información de tipo inferencial (deductiva) al observador sobre el comportamiento futuro del evento. La probabilidad a priori es especialmente importante en estadística bayesiana, donde la inferencia toma en cuenta los valores previos y posteriores al punto de observación. También es importante en áreas como filosofía del conocimiento.

Las probabilidades a priori permiten despejar un estado de incertidumbre inicial, evitar el sesgo inducido por la ausencia datos, y sanear datos previos desactualizados o mal distribuidos. Es importante diferenciar la probabilidad a priori –que refleja el conocimiento previo– de la probabilidad a posteriori, que se obtiene después de incorporar la nueva evidencia.

Un ejemplo de probabilidad previa, es la probabilidad de que una moneda desconocida caiga en "cara". Sin información sobre la moneda, aplicamos el principio de indiferencia: existen dos eventos posibles (cara o cruz), mutuamente excluyentes y con toda seguridad uno de ellos ocurrirá. Por lo tanto, la probabilidad a priori de obtener "cara" es 1/n, en este caso 1/2.

HSD

Probabilidad a priori en estadística bayesiana

Una distribución de probabilidad a priori de una cantidad incierta, a menudo llamada simplemente a priori , es su distribución de probabilidad asumida antes de que se tenga en cuenta alguna evidencia. Por ejemplo, el prior podría ser la distribución de probabilidad que representa las proporciones relativas de votantes que votarán por un político particular en una elección futura. La cantidad desconocida puede ser un parámetro del modelo o una variable latente en lugar de una variable observable.

En la estadística bayesiana, la regla de Bayes prescribe cómo actualizar la información anterior con nueva información para obtener la distribución de probabilidad posterior, que es la distribución condicional de la cantidad incierta dados los nuevos datos. Históricamente, la elección de priores a menudo se limitaba a una familia conjugada de una función de probabilidad dada, por lo que daría como resultado un posterior manejable de la misma familia. Sin embargo, la amplia disponibilidad de los métodos Monte Carlo de la cadena de Markov ha hecho que esto sea menos preocupante.

Hay muchas formas de construir una distribución previa. En algunos casos, se puede determinar un anterior a partir de información pasada, como experimentos anteriores. Un previo también puede obtenerse de la evaluación puramente subjetiva de un experto experimentado. Cuando no se disponga de información, podrá adoptarse un previo no informativo justificado por el principio de indiferencia. En las aplicaciones modernas, los prior también se eligen a menudo por sus propiedades mecánicas, como la regularización y la selección de características.

Las distribuciones previas de los parámetros del modelo a menudo dependerán de sus propios parámetros. La incertidumbre sobre estos hiperparámetros puede, a su vez, expresarse como distribuciones de probabilidad hiperprior. Por ejemplo, si se utiliza una distribución beta para modelar la distribución del parámetro p de una distribución de Bernoulli, entonces:

En principio, los priores se pueden descomponer en muchos niveles condicionales de distribuciones, los llamados priores jerárquicos.

Nivel de verosimilitud de la probabilidad a priori

A priori informativo

Un previo informativo expresa información específica y definida sobre una variable. Un ejemplo es una distribución previa de la temperatura de mañana al mediodía. Un enfoque razonable es hacer que la distribución anterior sea normal con un valor esperado igual a la temperatura del mediodía de hoy, con una varianza igual a la varianza diaria de la temperatura atmosférica, o una distribución de la temperatura para ese día del año.

Este ejemplo tiene una propiedad en común con muchos anteriores, a saber, que el posterior de un problema (la temperatura de hoy) se convierte en el anterior de otro problema (la temperatura de mañana); La evidencia preexistente que ya ha sido tomada en cuenta es parte de la anterior y, a medida que se acumula más evidencia, la posterior está determinada en gran medida por la evidencia más que por cualquier supuesto original, siempre que el supuesto original admitiera la posibilidad de lo que es la evidencia. sugerencia. Los términos "anterior" y "posterior" generalmente se refieren a un dato u observación específica.

A priori fuertemente informativo

Un a priori fuerte es un supuesto, teoría, concepto o idea precedente sobre el cual, después de tener en cuenta nueva información, se funda un supuesto, teoría, concepto o idea actual. Un previo fuerte es un tipo de previo informativo en el que la información contenida en la distribución previa domina la información contenida en los datos que se analizan. El análisis bayesiano combina la información contenida en la distribución anterior con la extraída de los datos para producir la distribución posterior que, en el caso de una "prior fuerte", cambiaría poco con respecto a la distribución anterior.

A priori débilmente informativo

Un previo débilmente informativo expresa información parcial sobre una variable, dirigiendo el análisis hacia soluciones que se alinean con el conocimiento existente sin limitar demasiado los resultados y evitar estimaciones extremas. Un ejemplo es, al establecer la distribución previa para la temperatura de mañana al mediodía en St. Louis, usar una distribución normal con una media de 50 grados Fahrenheit y una desviación estándar de 40 grados, lo que restringe muy vagamente la temperatura al rango (10 grados, 90 grados). grados) con una pequeña probabilidad de estar por debajo de -30 grados o por encima de 130 grados. El propósito de un prior débilmente informativo es la regularización, es decir, mantener las inferencias en un rango razonable.

A priori poco informativo

Un prior poco informativo , plano o difuso expresa información vaga o general sobre una variable. El término "anterior poco informativo" es un nombre poco apropiado. Tal a priori también podría denominarse a priori no muy informativo , o a priori objetivo , es decir, uno que no se obtiene subjetivamente.

Los antecedentes no informativos pueden expresar información "objetiva" como "la variable es positiva" o "la variable es menor que algún límite". La regla más simple y antigua para determinar un prior no informativo es el principio de indiferencia, que asigna probabilidades iguales a todas las posibilidades. En los problemas de estimación de parámetros, el uso de un a priori no informativo normalmente produce resultados que no son muy diferentes del análisis estadístico convencional, ya que la función de probabilidad a menudo produce más información que el a priori no informativo.

Se han hecho algunos intentos de encontrar probabilidades a priori, es decir, distribuciones de probabilidad en algún sentido lógicamente requeridas por la naturaleza del propio estado de incertidumbre; Estos son un tema de controversia filosófica, con los bayesianos divididos aproximadamente en dos escuelas: "bayesianos objetivos", que creen que tales antecedentes existen en muchas situaciones útiles, y "bayesianos subjetivos" que creen que en la práctica los antecedentes generalmente representan juicios de opinión subjetivos que no puede justificarse rigurosamente (Williamson 2010). Quizás los argumentos más sólidos a favor del bayesianismo objetivo los dio Edwin T. Jaynes, basándose principalmente en las consecuencias de las simetrías y en el principio de máxima entropía.

Como ejemplo de priori a priori, según Jaynes (2003), consideremos una situación en la que se sabe que una pelota ha estado escondida debajo de uno de tres vasos, A, B o C, pero no hay otra información disponible sobre su ubicación. . En este caso, un prior uniforme de p ( A ) = p ( B ) = p ( C ) = 1/3 parece intuitivamente la única opción razonable. Más formalmente, podemos ver que el problema sigue siendo el mismo si intercambiamos las etiquetas ("A", "B" y "C") de las tazas. Por lo tanto, sería extraño elegir un a priori para el cual una permutación de las etiquetas provocaría un cambio en nuestras predicciones sobre en qué copa se encontrará la pelota; el prior uniforme es el único que conserva esta invariancia. Si se acepta este principio de invariancia, entonces se puede ver que el previo uniforme es el previo lógicamente correcto para representar este estado de conocimiento. Este prior es "objetivo" en el sentido de ser la elección correcta para representar un estado particular de conocimiento, pero no es objetivo en el sentido de ser una característica del mundo independiente del observador: en realidad la pelota existe bajo una copa particular. , y sólo tiene sentido hablar de probabilidades en esta situación si hay un observador con conocimiento limitado sobre el sistema.

Como ejemplo más polémico, Jaynes publicó un argumento basado en la invariancia del previo bajo un cambio de parámetros que sugiere que el previo que representa una incertidumbre completa sobre una probabilidad debería ser el previo de Haldane p (1 −  p ) . El ejemplo que da Jaynes es el de encontrar una sustancia química en un laboratorio y preguntar si se disolverá en agua en experimentos repetidos. El prior de Haldane le da, con diferencia, el mayor peso a {\displaystyle p=0}y {\displaystyle p=1}, lo que indica que la muestra se disolverá cada vez o nunca se disolverá, con la misma probabilidad. Sin embargo, si se ha observado que las muestras de la sustancia química se disuelven en un experimento y no se disuelven en otro experimento, entonces este resultado previo se actualiza a la distribución uniforme en el intervalo [0, 1]. Esto se obtiene aplicando el teorema de Bayes al conjunto de datos que consta de una observación de disolución y otra de no disolución, utilizando lo anterior. El prior de Haldane es una distribución previa impropia (lo que significa que tiene una masa infinita). Harold Jeffreys ideó una forma sistemática de diseñar antecedentes no informativos como, por ejemplo, el previo de Jeffreys p (1 −  p ) para la variable aleatoria de Bernoulli.

Se pueden construir prioridades que sean proporcionales a la medida de Haar si el espacio de parámetros X lleva una estructura de grupo natural que deja invariante nuestro estado de conocimiento bayesiano. Esto puede verse como una generalización del principio de invariancia utilizado para justificar el prior uniforme sobre las tres copas en el ejemplo anterior. Por ejemplo, en física podríamos esperar que un experimento dé los mismos resultados independientemente de nuestra elección del origen de un sistema de coordenadas. Esto induce la estructura de grupo del grupo de traducción en X , lo que determina la probabilidad a priori como una a priori constante impropia. De manera similar, algunas medidas son naturalmente invariantes ante la elección de una escala arbitraria (por ejemplo, ya sea que se utilicen centímetros o pulgadas, los resultados físicos deben ser iguales). En tal caso, el grupo de escala es la estructura del grupo natural, y el prior correspondiente en X es proporcional a 1/ x . A veces importa si utilizamos la medida de Haar invariante por la izquierda o por la derecha. Por ejemplo, las medidas de Haar invariantes izquierda y derecha en el grupo afín no son iguales. Berger (1985, p. 413) sostiene que la medida de Haar invariante por la derecha es la elección correcta.

Otra idea, defendida por Edwin T. Jaynes, es utilizar el principio de máxima entropía (MAXENT). La motivación es que la entropía de Shannon de una distribución de probabilidad mide la cantidad de información contenida en la distribución. Cuanto mayor es la entropía, menos información proporciona la distribución. Por lo tanto, al maximizar la entropía sobre un conjunto adecuado de distribuciones de probabilidad en X , se encuentra la distribución que es menos informativa en el sentido de que contiene la menor cantidad de información consistente con las restricciones que definen el conjunto. Por ejemplo, la entropía máxima previa en un espacio discreto, dado solo que la probabilidad está normalizada a 1, es la previa que asigna igual probabilidad a cada estado. Y en el caso continuo, la entropía máxima previa, dado que la densidad está normalizada con media cero y varianza unitaria, es la distribución normal estándar. El principio de entropía cruzada mínima generaliza MAXENT al caso de "actualizar" una distribución previa arbitraria con restricciones adecuadas en el sentido de máxima entropía.

José-Miguel Bernardo introdujo una idea relacionada, los priores de referencia. Aquí, la idea es maximizar la divergencia esperada de Kullback-Leibler de la distribución posterior en relación con la anterior. Esto maximiza la información posterior esperada sobre X cuando la densidad previa es p ( x ); por lo tanto, en cierto sentido, p ( x ) es el a priori "menos informativo" sobre X. El a priori de referencia se define en el límite asintótico, es decir, se considera el límite de los a priori así obtenidos cuando el número de puntos de datos llega al infinito. . En el presente caso, la divergencia KL entre las distribuciones anterior y posterior viene dada por

{\displaystyle KL=\int p(t)\int p(x\mid t)\log {\frac {p(x\mid t)}{p(x)}}\,dx\,dt}

Aquí {\displaystyle t}hay una estadística suficiente para algún parámetro {\displaystyle x}. La integral interna es la divergencia KL entre las distribuciones anterior {\displaystyle p(x\mid t)}y posterior {\displaystyle p(x)}y el resultado es la media ponderada de todos los valores de {\displaystyle t}. Dividiendo el logaritmo en dos partes, invirtiendo el orden de las integrales en la segunda parte y observando que

{\displaystyle \log \,[p(x)]}

no depende de {\displaystyle t}los rendimientos

{\displaystyle KL=\int p(t)\int p(x\mid t)\log[p(x\mid t)]\,dx\,dt\,-\,\int \log[p(x )]\,\int p(t)p(x\mid t)\,dt\,dx}

La integral interna en la segunda parte es la integral {\displaystyle t}de la densidad conjunta {\displaystyle p(x,t)}. Esta es la distribución marginal {\displaystyle p(x)}, por lo que tenemos

{\displaystyle KL=\int p(t)\int p(x\mid t)\log[p(x\mid t)]\,dx\,dt\,-\,\int p(x)\log [p(x)]\,dx}

Ahora usamos el concepto de entropía que, en el caso de distribuciones de probabilidad, es el valor esperado negativo del logaritmo de la función de masa o densidad de probabilidad o {\displaystyle H(x)=-\int p(x)\log[p(x)]\,dx.} Usando esto en la última ecuación se obtiene

{\displaystyle KL=-\int p(t)H(x\mid t)\,dt+\,H(x)}

En palabras, KL es el valor esperado negativo {\displaystyle t}de la entropía de {\displaystyle x}condicional {\displaystyle t}más la entropía marginal (es decir, incondicional) de {\displaystyle x}. En el caso límite donde el tamaño de la muestra tiende al infinito, el teorema de Bernstein-von Mises establece que la distribución de {\displaystyle x}condicional a un valor observado dado de {\displaystyle t}es normal con una varianza igual al recíproco de la información de Fisher en el valor "verdadero" de {\displaystyle x}. La entropía de una función de densidad normal es igual a la mitad del logaritmo de {\displaystyle 2\pi ev}donde {\displaystyle v}está la varianza de la distribución. En este caso por lo tanto

{\displaystyle H=\log {\sqrt {2\pi e/[NI(x*)]}}}

donde {\displaystyle N}es el tamaño de muestra arbitrariamente grande (al cual la información de Fisher es proporcional) y {\displaystyle x*}es el valor "verdadero". Como esto no depende de {\displaystyle t}ello, se puede sacar de la integral, y como esta integral está sobre un espacio de probabilidad es igual a uno. Por tanto, podemos escribir la forma asintótica de KL como

{\displaystyle KL=-\log[1{\sqrt {kI(x*)}}]-\,\int p(x)\log[p(x)]\,dx}

donde {\displaystyle k}es proporcional al tamaño de la muestra (asintóticamente grande). No sabemos el valor de {\displaystyle x*}. De hecho, la idea misma va en contra de la filosofía de la inferencia bayesiana en la que los valores "verdaderos" de los parámetros son reemplazados por distribuciones previas y posteriores. Entonces lo eliminamos {\displaystyle x*}reemplazándolo con {\displaystyle x}y tomando el valor esperado de la entropía normal, que obtenemos multiplicando por {\displaystyle p(x)}e integrando {\displaystyle x}. Esto nos permite combinar los logaritmos dando

{\displaystyle KL=-\int p(x)\log[p(x)/{\sqrt {kI(x)}}]\,dx}

Se trata de una divergencia cuasi-KL ("cuasi" en el sentido de que la raíz cuadrada de la información de Fisher puede ser el núcleo de una distribución impropia). Debido al signo menos, debemos minimizarlo para maximizar la divergencia KL con la que comenzamos. El valor mínimo de la última ecuación ocurre cuando las dos distribuciones en el argumento del logaritmo, impropias o no, no divergen. Esto a su vez ocurre cuando la distribución previa es proporcional a la raíz cuadrada de la información de Fisher de la función de verosimilitud. Por lo tanto, en el caso de un solo parámetro, los antecedentes de referencia y los de Jeffreys son idénticos, aunque Jeffreys tiene una justificación muy diferente.

Los priores de referencia suelen ser los prioritarios objetivos de elección en problemas multivariados, ya que otras reglas (por ejemplo, la regla de Jeffreys) pueden dar lugar a prioritarios con comportamiento problemático.

Las distribuciones previas objetivas también pueden derivarse de otros principios, como la teoría de la información o la codificación (ver, por ejemplo, longitud mínima de la descripción) o estadísticas frecuentistas (las llamadas prioridades de coincidencia de probabilidad). Estos métodos se utilizan en la teoría de la inferencia inductiva de Solomonoff. La construcción de antecedentes objetivos se ha introducido recientemente en bioinformática, y especialmente en la inferencia en biología de sistemas cancerosos, donde el tamaño de la muestra es limitado y se encuentra disponible una gran cantidad de conocimiento previo . En estos métodos, se utiliza un criterio basado en la teoría de la información, como la divergencia KL o la función de probabilidad logarítmica para problemas de aprendizaje supervisado binario y problemas de modelos mixtos.

Los problemas filosóficos asociados con antecedentes poco informativos están asociados con la elección de una métrica o escala de medición adecuada. Supongamos que queremos una información previa para la velocidad de carrera de un corredor que no conocemos. Podríamos especificar, digamos, una distribución normal como prior para su velocidad, pero alternativamente podríamos especificar una prior normal para el tiempo que tarda en completar 100 metros, que es proporcional al recíproco de la primera prior. Se trata de antecedentes muy diferentes, pero no está claro cuál es el preferido. El método de Jaynes de transformación de grupos puede responder a esta pregunta en algunas situaciones.

De manera similar, si se nos pide que estimemos una proporción desconocida entre 0 y 1, podríamos decir que todas las proporciones son igualmente probables y utilizar un a priori uniforme. Alternativamente, podríamos decir que todos los órdenes de magnitud de la proporción son igualmente probables, laprior logarítmico , que es el prior uniforme del logaritmo de proporción. El a priori de Jeffreys intenta resolver este problema calculando un a priori que expresa la misma creencia sin importar qué métrica se utilice. La recomendación de Jeffreys para una proporción desconocidapesp(1 − p), que difiere de la recomendación de Jaynes.

Los a priori basados ​​en nociones de probabilidad algorítmica se utilizan en la inferencia inductiva como base para la inducción en entornos muy generales.

Los problemas prácticos asociados con antecedentes poco informativos incluyen el requisito de que la distribución posterior sea adecuada. Los habituales antecedentes poco informativos sobre variables continuas e ilimitadas son inadecuados. Esto no tiene por qué ser un problema si la distribución posterior es adecuada. Otra cuestión de importancia es que si se va a utilizar un previo no informativo de forma rutinaria , es decir, con muchos conjuntos de datos diferentes, debe tener buenas propiedades frecuentistas. Normalmente, a un bayesiano no le preocuparían estos problemas, pero puede ser importante en esta situación. Por ejemplo, uno querría que cualquier regla de decisión basada en la distribución posterior fuera admisible bajo la función de pérdida adoptada. Desafortunadamente, a menudo es difícil comprobar la admisibilidad, aunque se conocen algunos resultados (por ejemplo, Berger y Strawderman 1996). El problema es particularmente grave con los modelos jerárquicos de Bayes; los antecedentes habituales (por ejemplo, el de Jeffreys) pueden dar reglas de decisión muy inadmisibles si se emplean en los niveles más altos de la jerarquía.

A priori inadecuado

Dejemos que los eventos {\displaystyle A_{1},A_{2},\ldots,A_{n}}sean mutuamente excluyentes y exhaustivos. Si el teorema de Bayes se escribe como{\displaystyle P(A_{i}\mid B)={\frac {P(B\mid A_{i})P(A_{i})}{\sum _{j}P(B\mid A_{ j})P(A_{j})}}\,,}

entonces está claro que se obtendría el mismo resultado si todas las probabilidades anteriores P ( A i ) y P ( A j ) se multiplicaran por una constante dada; lo mismo sería cierto para una variable aleatoria continua. Si la suma en el denominador converge, las probabilidades posteriores aún sumarán (o se integrarán) a 1 incluso si los valores anteriores no lo hacen, por lo que es posible que solo sea necesario especificar los anteriores en la proporción correcta. Llevando esta idea más allá, en muchos casos es posible que la suma o integral de los valores anteriores ni siquiera necesite ser finita para obtener respuestas sensatas para las probabilidades posteriores. Cuando este es el caso, el prior se llama prior impropio . Sin embargo, la distribución posterior no tiene por qué ser una distribución adecuada si la anterior es incorrecta. Esto queda claro en el caso en el que el evento B es independiente de todos los A j .

Los estadísticos a veces utilizan antecedentes inadecuados como antecedentes no informativos. Por ejemplo, si necesitan una distribución previa para la media y la varianza de una variable aleatoria, pueden suponer p ( m ,  v ) ~ 1/ v (para v  > 0), lo que sugeriría que cualquier valor de la media es "igualmente igual". probable" y que un valor para la varianza positiva se vuelve "menos probable" en proporción inversa a su valor. Muchos autores (Lindley, 1973; De Groot, 1937; Kass y Wasserman, 1996) advierten contra el peligro de sobreinterpretar esos antecedentes, ya que no son densidades de probabilidad. La única relevancia que tienen se encuentra en el posterior correspondiente, siempre que esté bien definido para todas las observaciones. (El prior de Haldane es un contraejemplo típico ) .

Por el contrario, no es necesario integrar las funciones de probabilidad, y una función de probabilidad que es uniformemente 1 corresponde a la ausencia de datos (todos los modelos son igualmente probables si no hay datos): la regla de Bayes multiplica un a priori por la probabilidad, y un El producto vacío es solo la probabilidad constante 1. Sin embargo, sin comenzar con una distribución de probabilidad previa, no se termina obteniendo una distribución de probabilidad posterior y, por lo tanto, no se pueden integrar ni calcular los valores esperados o la pérdida. Consulte Función de probabilidad § No integrabilidad para obtener más detalles.

Ejemplos

Ejemplos de antecedentes inadecuados incluyen:

Estas funciones, interpretadas como distribuciones uniformes, también pueden interpretarse como la función de probabilidad en ausencia de datos, pero no son antecedentes adecuados.

Probabilidad a priori en mecánica estadística

La probabilidad a priori tiene una importante aplicación en la mecánica estadística. La versión clásica se define como la relación entre el número de eventos elementales (p. ej., el número de veces que se lanza un dado) y el número total de eventos, y estos se consideran puramente deductivos, es decir, sin experimentar. En el caso del dado, si lo miramos sobre la mesa sin tirarlo, se razona deductivamente que cada evento elemental tiene la misma probabilidad; por lo tanto, la probabilidad de cada resultado de un lanzamiento imaginario del dado (perfecto) o simplemente contando el número de caras es 1/6. Cada cara del dado aparece con la misma probabilidad, siendo la probabilidad una medida definida para cada evento elemental. El resultado es diferente si tiramos el dado veinte veces y preguntamos cuántas veces (de 20) aparece el número 6 en la cara superior. En este caso entra en juego el tiempo y tenemos un tipo diferente de probabilidad dependiendo del tiempo o del número de veces que se tire el dado. Por otro lado, la probabilidad a priori es independiente del tiempo, puedes mirar el dado sobre la mesa todo el tiempo que quieras sin tocarlo y deduces que la probabilidad de que aparezca el número 6 en la cara superior es 1/6.

En mecánica estadística, por ejemplo, la de un gas contenido en un volumen finito V, tanto las coordenadas espaciales { estilo de visualización q_ {i}}como las coordenadas de impulso Pi}de los elementos individuales del gas (átomos o moléculas) son finitas en el espacio de fase abarcado por estas coordenadas. En analogía con el caso del dado, la probabilidad a priori es aquí (en el caso de un continuo) proporcional al elemento de volumen del espacio de fase { estilo de visualización Delta q Delta p}dividido por h, y es el número de ondas estacionarias (es decir, estados) en él, donde { estilo de visualización Delta q}es el rango de la variable q y Delta pes el rango de la variable pags(aquí por simplicidad considerado en una dimensión). En 1 dimensión (longitud L) este número o peso estadístico o ponderación a priori es{ estilo de visualización L Delta p/h}. En las 3 dimensiones habituales (volumen V), el número correspondiente puede calcularse como {displaystyle V4pi p^{2}Delta p/h^{3}}. Para entender esta cantidad como dando un número de estados en la mecánica cuántica (es decir, ondulatoria), recuerde que en la mecánica cuántica cada partícula está asociada con una onda de materia que es la solución de una ecuación de Schrödinger. En el caso de partículas libres (de energía {displaystyle epsilon ={bf {p}}^{2}/2m}) como las de un gas en una caja de volumen {displaystyle V=L^{3}}tal onda de materia es explícitamente{displaystyle psi propto sin(lpi x/L)sin(mpi y/L)sin(npi z/L)},

donde { estilo de visualización l, m, n}están los números enteros. El número de { estilo de visualización (l, m, n)}valores diferentes y, por lo tanto, de estados en la región intermedia {displaystyle p,p+dp,p^{2}={bf {p}}^{2},}se encuentra entonces como la expresión anterior {displaystyle V4pi p^{2}dp/h^{3}}al considerar el área cubierta por estos puntos. Además, en vista de la relación de incertidumbre, que en 1 dimensión espacial es{ estilo de visualización Delta q Delta p geq h},

estos estados son indistinguibles (es decir, estos estados no llevan etiquetas). Una consecuencia importante es un resultado conocido como el teorema de Liouville, es decir, la independencia temporal de este elemento de volumen del espacio de fase y, por lo tanto, de la probabilidad a priori. Una dependencia temporal de esta cantidad implicaría información conocida sobre la dinámica del sistema y, por lo tanto, no sería una probabilidad a priori. Así la región{displaystyle Omega:={frac {Delta qDelta p}{int Delta qDelta p}},;;;int Delta qDelta p=const.,}

cuando se diferencia con respecto al tiempo tda cero (con la ayuda de las ecuaciones de Hamilton): El volumen en el tiempo tes el mismo que en el tiempo cero. Uno describe esto también como conservación de la información.

En la teoría cuántica completa se tiene una ley de conservación análoga. En este caso, la región del espacio de fases se reemplaza por un subespacio del espacio de estados expresado en términos de un operador de proyección PAGS, y en lugar de la probabilidad en el espacio de fases, se tiene la densidad de probabilidad{displaystyle Sigma:={frac {P}{{text{Tr}}(P)}},;;;N={text{Tr}}(P)=const.,}

donde nortees la dimensionalidad del subespacio. La ley de conservación en este caso se expresa por la unitaridad de la matriz S. En cualquier caso, las consideraciones asumen un sistema aislado cerrado. Este sistema aislado cerrado es un sistema con (1) una energía fija miy (2) un número fijo de partículasnorteen (c) un estado de equilibrio. Si se considera un gran número de réplicas de este sistema, se obtiene lo que se denomina un ``conjunto microcanónico''. Es para este sistema que se postula en estadística cuántica el ``postulado fundamental de probabilidades iguales a priori de un sistema aislado´´. Esto dice que el sistema aislado en equilibrio ocupa cada uno de sus estados accesibles con la misma probabilidad. Este postulado fundamental nos permite pues equiparar la probabilidad a priori a la degeneración de un sistema, es decir, al número de estados diferentes con la misma energía.

Ejemplos

El siguiente ejemplo ilustra la probabilidad a priori (o ponderación a priori) en contextos (a) clásicos y (b) cuánticos.

(a) Probabilidad clásica a priori

Considere la energía de rotación E de una molécula diatómica con momento de inercia I en coordenadas polares esféricas { estilo de visualización theta, phi}(esto significa qque arriba está aquí { estilo de visualización theta, phi}), es decir{displaystyle E={frac {1}{2I}}left(p_{theta }^{2}+{frac {p_{phi }^{2}}{sin ^{2} theta }}derecha).}

La { estilo de visualización (p_ { theta}, p_ { phi})}curva - para E constante y thetaes una elipse de área{displaystyle oint dp_{theta }dp_{phi }=pi {sqrt {2IE}}{sqrt {2IE}}sin theta =2pi IEsin theta }.

Integrando sobre thetay fiel volumen total del espacio de fase cubierto para energía constante E es{displaystyle int _{0}^{phi =2pi }int _{0}^{theta =pi }2Ipi Esin theta dtheta dphi =8pi ^{2}IE=oint dp_{theta }dp_{phi }dtheta dphi },

y, por lo tanto, la ponderación clásica a priori en el rango de energía { estilo de visualización dE}es{displaystyleOmegapropto} (volumen del espacio de fase en E+dE) menos (volumen del espacio de fase en mi) viene dado por{displaystyle 8{pi }^{2}IdE.}

(b) Probabilidad cuántica a priori

Suponiendo que el número de estados cuánticos en un rango { estilo de visualización Delta q Delta p}para cada dirección de movimiento está dado, por elemento, por un factor { estilo de visualización Delta q Delta p/h}, el número de estados en el rango de energía dE es, como se ve en (a) {displaystyle 8pi ^{2}IdE/h^{2}}para la molécula diatómica en rotación. De la mecánica ondulatoria se sabe que los niveles de energía de una molécula diatómica en rotación vienen dados por{displaystyle E_{n}={frac {n(n+1)h^{2}}{8pi ^{2}I}},}

siendo cada nivel de este tipo (2n+1) veces degenerado. Al evaluar {displaystyle dn/dE_{n}=1/(dE_{n}/dn)} se obtiene{displaystyle {frac {dn}{dE_{n}}}={frac {8pi ^{2}I}{(2n+1)h^{2}}},;;; (2n+1)dn={frac {8pi ^{2}I}{h^{2}}}dE_{n}.}

Así, en comparación con Omegalo anterior, se encuentra que el número aproximado de estados en el rango dE viene dado por la degeneración, es decir{ estilo de visualización Sigma propto (2n+1) dn.}

Así, la ponderación a priori en el contexto clásico (a) corresponde a la ponderación a priori aquí en el contexto cuántico (b). En el caso del oscilador armónico simple unidimensional de frecuencia natural, nuse encuentran correspondientemente: (a) {displaystyle Omega propto dE/nu }y (b) {displaystyle Sigma propto dn}(sin degeneración). Así, en mecánica cuántica, la probabilidad a priori es efectivamente una medida de la degeneración, es decir, el número de estados que tienen la misma energía.

En el caso del átomo de hidrógeno o potencial de Coulomb (donde la evaluación del volumen del espacio de fase para energía constante es más complicada) se sabe que la degeneración mecánica cuántica es n^{2}con {displaystyle Epropto 1/n^{2}}. Así en este caso {displaystyle Sigma propto n^{2}dn}.

Funciones de distribución en probabilidad a priori

En mecánica estadística (ver cualquier libro) se derivan las llamadas funciones de distribución Fpara varias estadísticas. En el caso de las estadísticas de Fermi-Dirac y las estadísticas de Bose-Einstein, estas funciones son respectivamente{displaystyle f_{i}^{FD}={frac {1}{e^{(epsilon_{i}-epsilon_{0})/kT}+1}},quad f_{i }^{BE}={frac {1}{e^{(epsilon _{i}-epsilon _{0})/kT}-1}}.}

Estas funciones se obtienen para (1) un sistema en equilibrio dinámico (es decir, en condiciones constantes y uniformes) con (2) un número total (y enorme) de partículas { Displaystyle N = Sigma _ {i} n_ {i}}(esta condición determina la constante epsilon _{0}), y (3) energía total {displaystyle E=Sigma_{i}n_{i}epsilon_{i}}, es decir, con cada una de las n_{yo}partículas que tiene la energía epsilon _{i}. Un aspecto importante en la derivación es tener en cuenta la indistinguibilidad de partículas y estados en estadística cuántica, es decir, allí partículas y estados no tienen etiquetas. En el caso de los fermiones, como los electrones, que obedecen al principio de Pauli (sólo una partícula por estado o ninguna permitida), se tiene por tanto{displaystyle 0leq f_{i}^{FD}leq 1,quad mientras quequad 0leq f_{i}^{BE}leq infty.}

Por lo tanto {displaystyle f_{i}^{FD}}, es una medida de la fracción de estados realmente ocupados por electrones a energía epsilon _{i}y temperatura T. Por otro lado, la probabilidad a priori soldado americano}es una medida del número de estados mecánicos ondulatorios disponibles. Por eso{displaystyle n_{i}=f_{i}g_{i}.}

Dado que n_{yo}es constante en condiciones uniformes (tantas partículas como las que salen de un elemento de volumen también entran de manera constante, de modo que la situación en el elemento parece estática), es decir, independiente del tiempo t, y soldado americano}también es independiente del tiempo t, como se mostró anteriormente, obtenemos{displaystyle {frac {df_{i}}{dt}}=0,quad f_{i}=f_{i}(t,{bf {v}}_{i},{bf {r }}_{i}).}

Expresando esta ecuación en términos de sus derivadas parciales, se obtiene la ecuación de transporte de Boltzmann. ¿Cómo aparecen aquí de repente las coordenadas, { estilo de visualización { bf {r}}}etc.? Arriba no se hizo mención de campos eléctricos o de otro tipo. Por lo tanto, sin tales campos presentes, tenemos la distribución de Fermi-Dirac como la anterior. Pero con tales campos presentes, tenemos esta dependencia adicional de F.