Distribución de probabilidad

Compartir Imprimir Citar

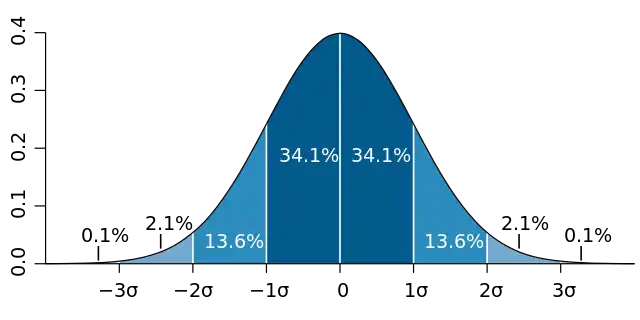
En teoría de probabilidad y estadística, una distribución de probabilidad es la función matemática que da las probabilidades de ocurrencia de diferentes resultados posibles para un experimento. Es una descripción matemática de un fenómeno aleatorio en términos de su espacio muestral y las probabilidades de eventos (subconjuntos del espacio muestral).

Por ejemplo, si se usa X para denotar el resultado de lanzar una moneda ("el experimento"), entonces la distribución de probabilidad de X tomaría el valor 0.5 (1 en 2 o 1/2) para X = cara, y 0.5 para X = cruz (asumiendo que la moneda es justa). Los ejemplos de fenómenos aleatorios incluyen las condiciones climáticas en una fecha futura, la altura de una persona seleccionada al azar, la fracción de estudiantes varones en una escuela, los resultados de una encuesta a realizar, etc.

Introducción

Una distribución de probabilidad es una descripción matemática de las probabilidades de eventos, subconjuntos del espacio muestral. El espacio muestral, a menudo denotado por $Omega$ , es el conjunto de todos los resultados posibles de un fenómeno aleatorio que se observa; puede ser cualquier conjunto: un conjunto de números reales, un conjunto de vectores, un conjunto de valores arbitrarios no numéricos, etc. Por ejemplo, el espacio muestral de un lanzamiento de moneda sería Ω = {cara, cruz}.

Para definir distribuciones de probabilidad para el caso específico de variables aleatorias (para que el espacio muestral pueda verse como un conjunto numérico), es común distinguir entre variables aleatorias discretas y absolutamente continuas. En el caso discreto, es suficiente especificar una función de masa de probabilidad que $pag$ asigne una probabilidad a cada resultado posible: por ejemplo, al lanzar un dado justo, cada uno de los seis valores del 1 al 6 tiene la probabilidad 1/6. Entonces, la probabilidad de un evento se define como la suma de las probabilidades de los resultados que satisfacen el evento; por ejemplo, la probabilidad del evento "el dado arroja un valor par" es

{displaystyle p(2)+p(4)+p(6)=1/6+1/6+1/6=1/2.}

Por el contrario, cuando una variable aleatoria toma valores de un continuo, por lo general, cualquier resultado individual tiene una probabilidad cero y solo los eventos que incluyen una cantidad infinita de resultados, como los intervalos, pueden tener una probabilidad positiva. Por ejemplo, considere medir el peso de una pieza de jamón en el supermercado y suponga que la báscula tiene muchos dígitos de precisión. La probabilidad de que pese exactamente 500 g es cero, ya que lo más probable es que tenga algunos dígitos decimales distintos de cero. Sin embargo, se podría exigir, en control de calidad, que un paquete de "500 g" de jamón debe pesar entre 490 g y 510 g con al menos un 98% de probabilidad, y esta exigencia es menos sensible a la precisión de los instrumentos de medición.

Las distribuciones de probabilidad absolutamente continuas se pueden describir de varias maneras. La función de densidad de probabilidad describe la probabilidad infinitesimal de cualquier valor dado, y la probabilidad de que el resultado se encuentre en un intervalo dado se puede calcular integrando la función de densidad de probabilidad en ese intervalo. Una descripción alternativa de la distribución es por medio de la función de distribución acumulativa, que describe la probabilidad de que la variable aleatoria no sea mayor que un valor dado. La función de distribución acumulativa es el área bajo la función de densidad de probabilidad desde $-infty$ hasta $X$ , como se describe en la imagen de la derecha.

Distribución de las probabilidades de la suma de dos dados en cada lanzada

Definición general de probabilidad

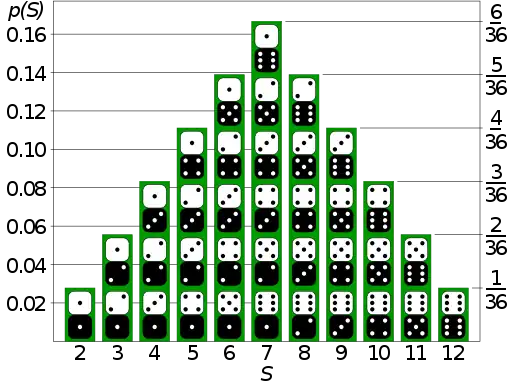
Una distribución de probabilidad se puede describir de varias formas, como una función de masa de probabilidad o una función de distribución acumulativa. Una de las descripciones más generales, que aplica para variables absolutamente continuas y discretas, es mediante una función de probabilidad ${displaystyle Pcolon {mathcal {A}}to mathbb {R} }$ cuyo espacio de entrada ${ matemáticas {A}}$ está relacionado con el espacio muestral, y da como salida una probabilidad de número real.

La función de probabilidad $PAG$ puede tomar como argumento subconjuntos del propio espacio muestral, como en el ejemplo del lanzamiento de una moneda, donde la función $PAG$ se definió de modo que P (cara) = 0,5 y P (cruz) = 0,5. Sin embargo, debido al uso generalizado de variables aleatorias, que transforman el espacio muestral en un conjunto de números (p. ej., $matemáticas {R}$ , $matemáticas {N}$ ), es más común estudiar distribuciones de probabilidad cuyos argumentos son subconjuntos de estos tipos particulares de conjuntos (conjuntos de números), y todas las distribuciones de probabilidad discutidas en este artículo son de este tipo. Es común denotar como ${ estilo de visualización P (X en E)}$ la probabilidad de que una determinada variable $X$ pertenezca a un determinado evento $mi$ .

La función de probabilidad anterior solo caracteriza una distribución de probabilidad si satisface todos los axiomas de Kolmogorov, es decir:

${displaystyle P(Xin E)geq 0;forall Ein {mathcal {A}}}$ , entonces la probabilidad es no negativa
${displaystyle P(Xin E)leq 1;forall Ein {mathcal {A}}}$ , por lo que ninguna probabilidad excede $1$
${displaystyle P(Xin bigsqcup_{i}E_{i})=sum_{i}P(Xin E_{i})}$ para cualquier familia disjunta de conjuntos ${E_{i}}$

El concepto de función de probabilidad se hace más riguroso al definirlo como el elemento de un espacio de probabilidad ${displaystyle (X,{mathcal {A}},P)}$ , donde $X$ es el conjunto de resultados posibles, ${ matemáticas {A}}$ es el conjunto de todos los subconjuntos $Esubconjunto X$ cuya probabilidad se puede medir, y $PAG$ es la función de probabilidad, o medida de probabilidad, que asigna una probabilidad a cada uno de estos subconjuntos medibles ${displaystyle Ein {mathcal {A}}}$ .

Las distribuciones de probabilidad generalmente pertenecen a una de dos clases. Una distribución de probabilidad discreta es aplicable a los escenarios donde el conjunto de posibles resultados es discreto (por ejemplo, lanzar una moneda al aire, tirar un dado) y las probabilidades están codificadas por una lista discreta de las probabilidades de los resultados; en este caso, la distribución de probabilidad discreta se conoce como función de masa de probabilidad. Por otro lado, las distribuciones de probabilidad absolutamente continuasson aplicables a escenarios en los que el conjunto de resultados posibles puede tomar valores en un rango continuo (por ejemplo, números reales), como la temperatura en un día determinado. En el caso absolutamente continuo, las probabilidades se describen mediante una función de densidad de probabilidad, y la distribución de probabilidad es, por definición, la integral de la función de densidad de probabilidad. La distribución normal es una distribución de probabilidad absolutamente continua comúnmente encontrada. Los experimentos más complejos, como los que implican procesos estocásticos definidos en tiempo continuo, pueden exigir el uso de medidas de probabilidad más generales.

Una distribución de probabilidad cuyo espacio muestral es unidimensional (por ejemplo, números reales, lista de etiquetas, etiquetas ordenadas o binaria) se denomina univariante, mientras que una distribución cuyo espacio muestral es un espacio vectorial de dimensión 2 o más se denomina multivariante. Una distribución univariada da las probabilidades de que una sola variable aleatoria tome varios valores diferentes; una distribución multivariante (una distribución de probabilidad conjunta) da las probabilidades de un vector aleatorio (una lista de dos o más variables aleatorias) que toman varias combinaciones de valores. Las distribuciones de probabilidad univariadas importantes y comúnmente encontradas incluyen la distribución binomial, la distribución hipergeométrica y la distribución normal. Una distribución multivariante que se encuentra comúnmente es la distribución normal multivariante.

Además de la función de probabilidad, la función de distribución acumulativa, la función de masa de probabilidad y la función de densidad de probabilidad, la función generadora de momentos y la función característica también sirven para identificar una distribución de probabilidad, ya que determinan únicamente una función de distribución acumulativa subyacente.

Terminología

A continuación se enumeran algunos conceptos y términos clave, ampliamente utilizados en la literatura sobre el tema de las distribuciones de probabilidad.

Términos básicos

Variable aleatoria: toma valores de un espacio muestral; las probabilidades describen qué valores y conjunto de valores se toman con mayor probabilidad.
Evento: conjunto de posibles valores (resultados) de una variable aleatoria que ocurre con cierta probabilidad.
Función de probabilidad o medida de probabilidad: describe la probabilidad ${ estilo de visualización P (X en E)}$ de que ocurra el evento ${ estilo de visualización E,}$ .
Función de distribución acumulativa: función que evalúa la probabilidad de que $X$ tome un valor menor o igual que $X$ para una variable aleatoria (solo para variables aleatorias de valor real).
Función cuantil: la inversa de la función de distribución acumulada. Da $X$ tal que, con probabilidad $q$ , $X$ no excederá de $X$ .

Distribuciones de probabilidad discretas

Distribución de probabilidad discreta: para muchas variables aleatorias con un número finito o contable infinito de valores.
Función de masa de probabilidad (pmf): función que da la probabilidad de que una variable aleatoria discreta sea igual a algún valor.
Distribución de frecuencia: una tabla que muestra la frecuencia de varios resultados en una muestra.
Distribución de frecuencias relativas: una distribución de frecuencias en la que cada valor se ha dividido (normalizado) por un número de resultados en una muestra (es decir, el tamaño de la muestra).
Distribución categórica: para variables aleatorias discretas con un conjunto finito de valores.

Distribuciones de probabilidad absolutamente continuas

Distribución de probabilidad absolutamente continua: para muchas variables aleatorias con innumerables valores.
Función de densidad de probabilidad (pdf) o Densidad de probabilidad: función cuyo valor en cualquier muestra dada (o punto) en el espacio muestral (el conjunto de valores posibles tomados por la variable aleatoria) puede interpretarse como que proporciona una probabilidad relativa de que el valor de la variable aleatoria sería igual a esa muestra.

Términos relacionados

Soporte: conjunto de valores que pueden ser asumidos con probabilidad distinta de cero por la variable aleatoria. Para una variable aleatoria $X$ , a veces se denota como $R_{X}$ .
Cola: las regiones cercanas a los límites de la variable aleatoria, si el pmf o pdf son relativamente bajos allí. Suele tener la forma un X o una unión de las mismas.
Head: la región donde el pmf o pdf es relativamente alto. Suele tener la forma <img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d355c5d91dc6c206477bbc961ef58b3f96f9fbcd" alt="{ estilo de visualización a <X .
Valor esperado o media: la media ponderada de los valores posibles, utilizando sus probabilidades como pesos; o el análogo continuo del mismo.
Mediana: el valor tal que el conjunto de valores menores que la mediana y el conjunto mayor que la mediana, cada uno tiene probabilidades no mayores a la mitad.
Moda: para una variable aleatoria discreta, el valor con mayor probabilidad; para una variable aleatoria absolutamente continua, una ubicación en la que la función de densidad de probabilidad tiene un pico local.
Cuantil: el q-cuantil es el valor $X$ tal que
Varianza: el segundo momento de la pmf o pdf respecto a la media; una medida importante de la dispersión de la distribución.
Desviación estándar: la raíz cuadrada de la varianza y, por lo tanto, otra medida de dispersión.
Simetría: una propiedad de algunas distribuciones en la que la porción de la distribución a la izquierda de un valor específico (generalmente la mediana) es una imagen especular de la porción a su derecha.
Asimetría: una medida de la medida en que un pmf o pdf se "inclina" hacia un lado de su media. El tercer momento estandarizado de la distribución.
Curtosis: una medida de la "gordura" de las colas de un pmf o pdf. El cuarto momento estandarizado de la distribución.

Explicación de un gráficos de distribución acumulativa

Función de distribución acumulativa

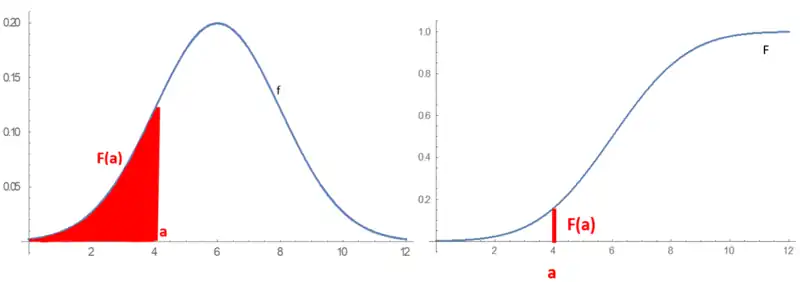
En el caso especial de una variable aleatoria de valor real, la distribución de probabilidad puede representarse de manera equivalente mediante una función de distribución acumulativa en lugar de una medida de probabilidad. La función de distribución acumulada de una variable aleatoria $X$ con respecto a una distribución de probabilidad $pag$ se define como

La función de distribución acumulativa de cualquier variable aleatoria de valor real tiene las propiedades:

$F(x)$ no es decreciente;
$F(x)$ es continua por la derecha;
${ estilo de visualización 0 leq F (x) leq 1}$ ;
${displaystyle lim _{xto -infty}F(x)=0}$ y ${displaystyle lim _{xto infty}F(x)=1}$ ; y
<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8cd4cd12484aa3aec4ef24ee66a34edd9df105b1" alt="{displaystyle Pr(a.

Por el contrario, cualquier función ${displaystyle F:mathbb {R} to mathbb {R} }$ que satisfaga las primeras cuatro de las propiedades anteriores es la función de distribución acumulativa de alguna distribución de probabilidad de los números reales.

Cualquier distribución de probabilidad se puede descomponer como la suma de una distribución discreta, una absolutamente continua y una continua singular, por lo que cualquier función de distribución acumulativa admite una descomposición como la suma de las tres funciones de distribución acumulativas correspondientes.

Distribución de probabilidad discreta

Una distribución de probabilidad discreta es la distribución de probabilidad de una variable aleatoria que puede tomar solo un número contable de valores (casi con seguridad), lo que significa que la probabilidad de cualquier evento $mi$ puede expresarse como una suma (finita o numerablemente infinita):

{displaystyle P(Xin E)=sum _{omega in A}P(X=omega),}

donde $UN$ es un conjunto contable. Por lo tanto, las variables aleatorias discretas son exactamente aquellas con una función de masa de probabilidad ${ estilo de visualización p (x) = P (X = x)}$ . En el caso de que el rango de valores sea contablemente infinito, estos valores tienen que declinar a cero lo suficientemente rápido para que las probabilidades sumen 1. Por ejemplo, si ${displaystyle p(n)={tfrac {1}{2^{n}}}}$ para ${ estilo de visualización n = 1,2,...}$ , la suma de probabilidades sería ${displaystyle 1/2+1/4+1/8+puntos =1}$ .

Una variable aleatoria discreta es una variable aleatoria cuya distribución de probabilidad es discreta.

Las distribuciones de probabilidad discreta bien conocidas utilizadas en el modelado estadístico incluyen la distribución de Poisson, la distribución de Bernoulli, la distribución binomial, la distribución geométrica, la distribución binomial negativa y la distribución categórica. Cuando se extrae una muestra (un conjunto de observaciones) de una población más grande, los puntos de muestra tienen una distribución empírica que es discreta y que proporciona información sobre la distribución de la población. Además, la distribución uniforme discreta se usa comúnmente en programas de computadora que hacen selecciones aleatorias de igual probabilidad entre varias opciones.

Función de distribución acumulativa

Una variable aleatoria discreta de valor real se puede definir de manera equivalente como una variable aleatoria cuya función de distribución acumulativa aumenta solo por discontinuidades de salto, es decir, su cdf aumenta solo donde "salta" a un valor más alto y es constante en intervalos sin saltos. Los puntos donde se producen los saltos son precisamente los valores que puede tomar la variable aleatoria. Así, la función de distribución acumulada tiene la forma

{displaystyle F(x)=P(Xleq x)=sum _{omega leq x}p(omega).}

Tenga en cuenta que los puntos donde salta la cdf siempre forman un conjunto contable; este puede ser cualquier conjunto contable y, por lo tanto, incluso puede ser denso en los números reales.

Representación delta de Dirac

Una distribución de probabilidad discreta a menudo se representa con medidas de Dirac, las distribuciones de probabilidad de variables aleatorias deterministas. Para cualquier resultado $omega$ , ${ estilo de visualización delta _ { omega}}$ sea la medida de Dirac concentrada en $omega$ . Dada una distribución de probabilidad discreta, existe un conjunto contable $UN$ con ${displaystyle P(Xen A)=1}$ una función de masa de probabilidad $pag$ . Si $mi$ es cualquier evento, entonces

{displaystyle P(Xin E)=sum_{omega in A}p(omega)delta_{omega }(E),}

o en resumen,

{displaystyle P_{X}=sum_{omega in A}p(omega)delta_{omega }.}

De manera similar, las distribuciones discretas se pueden representar con la función delta de Dirac como una función de densidad de probabilidad generalizada $F$ , donde

{displaystyle f(x)=sum_{omega in A}p(omega)delta (x-omega),}

lo que significa

{displaystyle P(Xin E)=int_{E}f(x),dx=sum_{omega in A}p(omega)int_{E}delta (x -omega)=sum _{omega in Acap E}p(omega)}

para cualquier evento $MI.$

Representación indicador-función

Para una variable aleatoria discreta $X$ , ${displaystyle u_{0},u_{1},puntos}$ sean los valores que puede tomar con probabilidad distinta de cero. Denotar

{displaystyle Omega _{i}=X^{-1}(u_{i})={omega:X(omega)=u_{i}},,i=0,1,2,puntos }

Estos son conjuntos disjuntos, y para tales conjuntos

{displaystyle Pleft(bigcup_{i}Omega_{i}right)=sum_{i}P(Omega_{i})=sum_{i}P(X=u_ {i})=1.}

De ello se deduce que la probabilidad que $X$ toma cualquier valor excepto ${displaystyle u_{0},u_{1},puntos}$ es cero, y por lo tanto se puede escribir $X$ como

{displaystyle X(omega)=sum _{i}u_{i}1_{Omega _{i}}(omega)}

excepto en un conjunto de probabilidad cero, donde $1_{A}$ es la función indicadora de $UN$ . Esto puede servir como una definición alternativa de variables aleatorias discretas.

Distribución de un punto

Un caso especial es la distribución discreta de una variable aleatoria que sólo puede tomar un valor fijo; en otras palabras, es una distribución determinista. Expresada formalmente, la variable aleatoria $X$ tiene una distribución de un punto si tiene un resultado posible $X$ tal que ${displaystyle P(X{=}x)=1.}$ Todos los demás resultados posibles tienen probabilidad 0. Su función de distribución acumulada salta inmediatamente de 0 a 1.

Distribución de probabilidad absolutamente continua

Una distribución de probabilidad absolutamente continua es una distribución de probabilidad de los números reales con innumerables valores posibles, como un intervalo completo en la línea real, y donde la probabilidad de cualquier evento se puede expresar como una integral. Más precisamente, una variable aleatoria real $X$ tiene una distribución de probabilidad absolutamente continua si existe una función ${displaystyle f:mathbb {R} a [0,infty]}$ tal que para cada intervalo ${displaystyle [a,b]subconjunto mathbb {R} }$ la probabilidad de $X$ pertenecer a $[a,b]$ está dada por la integral de $F$ sobre $yo$ :

{displaystyle Pleft(aleq Xleq bright)=int _{a}^{b}f(x),dx.}

Esta es la definición de una función de densidad de probabilidad, de modo que las distribuciones de probabilidad absolutamente continuas son exactamente aquellas con una función de densidad de probabilidad. En particular, la probabilidad de $X$ tomar cualquier valor único $un$ (es decir, ${displaystyle aleq Xleq a}$ ) es cero, porque una integral con límites superior e inferior coincidentes siempre es igual a cero. Si el intervalo $[a,b]$ se reemplaza por cualquier conjunto medible $UN$ , la igualdad correspondiente sigue siendo válida:

{displaystyle P(Xin A)=int _{A}f(x),dx.}

Una variable aleatoria absolutamente continua es una variable aleatoria cuya distribución de probabilidad es absolutamente continua.

Hay muchos ejemplos de distribuciones de probabilidad absolutamente continuas: normal, uniforme, chi-cuadrado y otras.

Función de distribución acumulativa

Las distribuciones de probabilidad absolutamente continuas, tal como se definen anteriormente, son precisamente aquellas con una función de distribución acumulativa absolutamente continua. En este caso, la función de distribución acumulada $F$ tiene la forma

{displaystyle F(x)=P(Xleq x)=int_{-infty}^{x}f(t),dt}

donde $F$ es una densidad de la variable aleatoria $X$ con respecto a la distribución $PAG$ .

Nota sobre la terminología: Deben distinguirse las distribuciones absolutamente continuas de las distribuciones continuas, que son aquellas que tienen una función de distribución acumulativa continua. Toda distribución absolutamente continua es una distribución continua pero no ocurre lo contrario, existen distribuciones singulares, que no son ni absolutamente continuas ni discretas ni una mezcla de ellas, y no tienen densidad. Un ejemplo lo da la distribución de Cantor. Sin embargo, algunos autores utilizan el término "distribución continua" para indicar todas las distribuciones cuya función de distribución acumulativa es absolutamente continua, es decir, se refieren a las distribuciones absolutamente continuas como distribuciones continuas.

Para obtener una definición más general de las funciones de densidad y las medidas absolutamente continuas equivalentes, consulte medida absolutamente continua.

Kolmogorov definición

En la formalización teórica de la medida de la teoría de la probabilidad, una variable aleatoria se define como una función medible $X$ de un espacio de probabilidad $(Omega,{mathcal {F}},mathbb {P})$ a un espacio medible ${displaystyle ({mathcal {X}},{mathcal {A}})}$ . Dado que las probabilidades de eventos de la forma ${displaystyle {omega in Omega mid X(omega)in A}}$ satisfacen los axiomas de probabilidad de Kolmogorov, la distribución de probabilidad de es la medida ${displaystyle X_{*}mathbb {P} }$ de avance de $X$ , que es una medida de probabilidad al ${displaystyle ({mathcal {X}},{mathcal {A}})}$ satisfacer ${displaystyle X_{*}mathbb {P} =mathbb {P} X^{-1}}$ .

Otros tipos de distribuciones

Las distribuciones absolutamente continuas y discretas con soporte en $mathbb{R} ^{k}$ o ${ matemáticas {N}}^{k}$ son extremadamente útiles para modelar una miríada de fenómenos, ya que la mayoría de las distribuciones prácticas se apoyan en subconjuntos relativamente simples, como hipercubos o bolas. Sin embargo, esto no siempre es así, y existen fenómenos con soportes que en realidad son curvas complicadas ${displaystyle gamma:[a,b]rightarrow mathbb {R} ^{n}}$ dentro de algún espacio $mathbb{R} ^{n}$ o similar. En estos casos, la distribución de probabilidad se basa en la imagen de dicha curva y es probable que se determine empíricamente, en lugar de encontrar una fórmula cerrada para ella.

En la figura de la derecha se muestra un ejemplo, que muestra la evolución de un sistema de ecuaciones diferenciales (comúnmente conocidas como ecuaciones de Rabinovich-Fabrikant) que se pueden usar para modelar el comportamiento de las ondas de Langmuir en el plasma. Cuando se estudia este fenómeno, los estados observados del subconjunto se indican en rojo. Entonces uno podría preguntarse cuál es la probabilidad de observar un estado en cierta posición del subconjunto rojo; si tal probabilidad existe, se llama la medida de probabilidad del sistema.

Este tipo de soporte complicado aparece con bastante frecuencia en los sistemas dinámicos. No es sencillo establecer que el sistema tiene una medida de probabilidad, y el principal problema es el siguiente. Sean ${displaystyle t_{1}ll t_{2}ll t_{3}}$ instantes en el tiempo y $O$ un subconjunto del soporte; si la medida de probabilidad existe para el sistema, uno esperaría que la frecuencia de observar estados dentro del conjunto $O$ fuera igual en el intervalo ${ estilo de visualización [t_{1},t_{2}]}$ y ${ estilo de visualización [t_{2},t_{3}]}$ , lo que podría no suceder; por ejemplo, podría oscilar similar a un seno $sin(t)$ , cuyo límite cuando $trightarrowinfty$ no converge. Formalmente, la medida existe solo si el límite de la frecuencia relativa converge cuando se observa el sistema en el futuro infinito.La rama de los sistemas dinámicos que estudia la existencia de una medida de probabilidad es la teoría ergódica.

Tenga en cuenta que incluso en estos casos, la distribución de probabilidad, si existe, podría denominarse "absolutamente continua" o "discreta", dependiendo de si el soporte es contable o no contable, respectivamente.

Generación de números aleatorios

La mayoría de los algoritmos se basan en un generador de números pseudoaleatorios que produce números $X$ que se distribuyen uniformemente en el intervalo semiabierto [0, 1). Estas variables aleatorias $X$ luego se transforman a través de algún algoritmo para crear una nueva variable aleatoria que tenga la distribución de probabilidad requerida. Con esta fuente de seudoaleatoriedad uniforme, se pueden generar realizaciones de cualquier variable aleatoria.

Por ejemplo, supongamos que $tu$ tiene una distribución uniforme entre 0 y 1. Para construir una variable aleatoria de Bernoulli para alguna <img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ea074f5b36db6eff17f1aa84d73e30e3de12c4d6" alt="0<p, definimos

<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/71a1cc9754e3861243bd6e273fc171cc6fda008a" alt="{displaystyle X={begin{casos}1,&{text{si}}U

así que eso

<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ea5c250e1de914d6e1d78e9397f146f676cef41b" alt="{displaystyle Pr(X=1)=Pr(U

Esta variable aleatoria X tiene una distribución de Bernoulli con parámetro $pag$ . Tenga en cuenta que esta es una transformación de variable aleatoria discreta.

Para una función de distribución $F$ de una variable aleatoria absolutamente continua, se debe construir una variable aleatoria absolutamente continua. ${displaystyle F^{mathit {inv}}}$ , una función inversa de $F$ , se relaciona con la variable uniforme $tu$ :

{displaystyle {Uleq F(x)}={F^{mathit {inv}}(U)leq x}.}

${displaystyle F(x)=1-e^{-lambda x}}$ Por ejemplo, suponga que se debe construir una variable aleatoria que tiene una distribución exponencial.

{displaystyle {begin{alineado}F(x)=u&Leftrightarrow 1-e^{-lambda x}=u\[2pt]&Leftrightarrow e^{-lambda x}=1-u [2pt]&Leftrightarrow -lambda x=ln(1-u)\[2pt]&Leftrightarrow x={frac {-1}{lambda }}ln(1-u)end {alineado}}}

entonces ${displaystyle F^{mathit {inv}}(u)={frac {-1}{lambda}}ln(1-u)}$ y si $tu$ tiene una $tu(0,1)$ distribución, entonces la variable aleatoria $X$ está definida por ${displaystyle X=F^{mathit {inv}}(U)={frac {-1}{lambda}}ln(1-U)}$ . Esto tiene una distribución exponencial de $lambda$ .

Un problema frecuente en las simulaciones estadísticas (método de Monte Carlo) es la generación de números pseudoaleatorios que se distribuyen de una forma determinada.

Distribuciones de probabilidad comunes y sus aplicaciones

El concepto de la distribución de probabilidad y las variables aleatorias que describen subyace en la disciplina matemática de la teoría de la probabilidad y la ciencia de la estadística. Hay dispersión o variabilidad en casi cualquier valor que pueda medirse en una población (por ejemplo, la altura de las personas, la durabilidad de un metal, el crecimiento de las ventas, el flujo de tráfico, etc.); casi todas las mediciones se realizan con algún error intrínseco; en física, muchos procesos se describen probabilísticamente, desde las propiedades cinéticas de los gases hasta la descripción mecánica cuántica de las partículas fundamentales. Por estas y muchas otras razones, los números simples a menudo son inadecuados para describir una cantidad, mientras que las distribuciones de probabilidad suelen ser más apropiadas.

La siguiente es una lista de algunas de las distribuciones de probabilidad más comunes, agrupadas por el tipo de proceso con el que están relacionadas. Para obtener una lista más completa, consulte la lista de distribuciones de probabilidad, que se agrupa por la naturaleza del resultado que se considera (discreto, absolutamente continuo, multivariante, etc.)

Todas las distribuciones univariadas a continuación tienen un solo pico; es decir, se supone que los valores se agrupan alrededor de un solo punto. En la práctica, las cantidades realmente observadas pueden agruparse en torno a múltiples valores. Tales cantidades se pueden modelar utilizando una distribución de mezcla.

Crecimiento lineal (por ejemplo, errores, compensaciones)

Distribución normal (distribución gaussiana), para una sola cantidad; la distribución absolutamente continua más utilizada

Crecimiento exponencial (por ejemplo, precios, ingresos, poblaciones)

Distribución logarítmica normal, para una sola cantidad cuyo logaritmo se distribuye normalmente
Distribución de Pareto, para una sola cantidad cuyo logaritmo se distribuye exponencialmente; la distribución prototípica de la ley de potencias

Cantidades uniformemente distribuidas

Distribución uniforme discreta, para un conjunto finito de valores (por ejemplo, el resultado de un dado justo)
Distribución uniforme continua, para valores distribuidos absolutamente continuos

Pruebas de Bernoulli (eventos sí/no, con una probabilidad dada)

Distribuciones básicas:
- Distribución de Bernoulli, para el resultado de un solo ensayo de Bernoulli (por ejemplo, éxito/fracaso, sí/no)
- Distribución binomial, para el número de "ocurrencias positivas" (por ejemplo, éxitos, votos a favor, etc.) dado un número total fijo de ocurrencias independientes
- Distribución binomial negativa, para observaciones de tipo binomial pero donde la cantidad de interés es la cantidad de fallas antes de que ocurra una cantidad determinada de éxitos
- Distribución geométrica, para observaciones de tipo binomial pero donde la cantidad de interés es el número de fallas antes del primer éxito; un caso especial de la distribución binomial negativa
Relacionado con esquemas de muestreo sobre una población finita:
- Distribución hipergeométrica, para el número de "ocurrencias positivas" (por ejemplo, éxitos, votos a favor, etc.) dado un número fijo de ocurrencias totales, usando muestreo sin reemplazo
- Distribución beta-binomial, para el número de "ocurrencias positivas" (por ejemplo, éxitos, votos a favor, etc.) dado un número fijo de ocurrencias totales, muestreo utilizando un modelo de urna de Pólya (en cierto sentido, el "opuesto" de muestreo sin reemplazo)

Resultados categóricos (eventos con K resultados posibles)

Distribución categórica, para un único resultado categórico (por ejemplo, sí/no/tal vez en una encuesta); una generalización de la distribución de Bernoulli
Distribución multinomial, para el número de cada tipo de resultado categórico, dado un número fijo de resultados totales; una generalización de la distribución binomial
Distribución hipergeométrica multivariada, similar a la distribución multinomial, pero usando muestreo sin reemplazo; una generalización de la distribución hipergeométrica

Proceso de Poisson (eventos que ocurren independientemente con una tasa dada)

Distribución de Poisson, para el número de ocurrencias de un evento de tipo Poisson en un período de tiempo determinado
Distribución exponencial, para el tiempo antes de que ocurra el próximo evento de tipo Poisson
Distribución gamma, para el tiempo antes de que ocurran los próximos k eventos de tipo Poisson

Valores absolutos de vectores con componentes distribuidos normalmente

Distribución de Rayleigh, para la distribución de magnitudes vectoriales con componentes ortogonales distribuidas en Gauss. Las distribuciones de Rayleigh se encuentran en señales de RF con componentes reales e imaginarias gaussianas.
Distribución de Rice, una generalización de las distribuciones de Rayleigh para donde hay un componente de señal de fondo estacionario. Se encuentra en el desvanecimiento de señales de radio de Rician debido a la propagación de trayectos múltiples y en imágenes de RM con corrupción de ruido en señales de RMN distintas de cero.

Cantidades distribuidas normalmente operadas con suma de cuadrados

Distribución de chi-cuadrado, la distribución de una suma de variables normales estándar al cuadrado; útil, por ejemplo, para la inferencia con respecto a la varianza de la muestra de muestras distribuidas normalmente (consulte la prueba de chi-cuadrado)
distribución t de Student, la distribución de la razón de una variable normal estándar y la raíz cuadrada de una variable chi cuadrada escalada; útil para la inferencia con respecto a la media de muestras distribuidas normalmente con varianza desconocida (consulte la prueba t de Student)
Distribución F, la distribución de la razón de dos variables de chi cuadrado escaladas; útil, por ejemplo, para inferencias que impliquen comparar varianzas o R-cuadrado (el coeficiente de correlación al cuadrado)

Como distribuciones previas conjugadas en la inferencia bayesiana

Distribución Beta, para una sola probabilidad (número real entre 0 y 1); conjugado a la distribución de Bernoulli y distribución binomial
Distribución gamma, para un parámetro de escala no negativo; conjugado con el parámetro de tasa de una distribución de Poisson o distribución exponencial, la precisión (varianza inversa) de una distribución normal, etc.
Distribución de Dirichlet, para un vector de probabilidades que debe sumar 1; conjugado a la distribución categórica y distribución multinomial; generalización de la distribución beta
Distribución de Wishart, para una matriz definida simétrica no negativa; conjugado a la inversa de la matriz de covarianza de una distribución normal multivariante; generalización de la distribución gamma

Algunas aplicaciones especializadas de las distribuciones de probabilidad

Los modelos de lenguaje de caché y otros modelos de lenguaje estadístico utilizados en el procesamiento del lenguaje natural para asignar probabilidades a la ocurrencia de palabras y secuencias de palabras particulares lo hacen por medio de distribuciones de probabilidad.
En mecánica cuántica, la densidad de probabilidad de encontrar la partícula en un punto dado es proporcional al cuadrado de la magnitud de la función de onda de la partícula en ese punto (ver regla de Born). Por lo tanto, la función de distribución de probabilidad de la posición de una partícula está descrita por ${textstyle P_{aleq xleq b}(t)=int _{a}^{b}dx,|Psi (x,t)|^{2}}$ , probabilidad de que la posición x de la partícula esté en el intervalo a ≤ x ≤ b en la dimensión uno, y una integral triple similar en la dimensión tres. Este es un principio clave de la mecánica cuántica.
El flujo de carga probabilístico en el estudio de flujo de potencia explica las incertidumbres de las variables de entrada como distribución de probabilidad y proporciona el cálculo del flujo de potencia también en términos de distribución de probabilidad.
Predicción de ocurrencias de fenómenos naturales en base a distribuciones de frecuencias previas como ciclones tropicales, granizo, tiempo entre eventos, etc.

Distribución de probabilidad

Introducción

Definición general de probabilidad

Terminología

Términos básicos

Distribuciones de probabilidad discretas

Distribuciones de probabilidad absolutamente continuas

Términos relacionados

Función de distribución acumulativa

Distribución de probabilidad discreta

Función de distribución acumulativa

Representación delta de Dirac

Representación indicador-función

Distribución de un punto

Distribución de probabilidad absolutamente continua

Función de distribución acumulativa

Kolmogorov definición

Otros tipos de distribuciones

Generación de números aleatorios

Distribuciones de probabilidad comunes y sus aplicaciones

Crecimiento lineal (por ejemplo, errores, compensaciones)

Crecimiento exponencial (por ejemplo, precios, ingresos, poblaciones)

Cantidades uniformemente distribuidas

Pruebas de Bernoulli (eventos sí/no, con una probabilidad dada)

Resultados categóricos (eventos con K resultados posibles)

Proceso de Poisson (eventos que ocurren independientemente con una tasa dada)

Valores absolutos de vectores con componentes distribuidos normalmente

Cantidades distribuidas normalmente operadas con suma de cuadrados

Como distribuciones previas conjugadas en la inferencia bayesiana

Algunas aplicaciones especializadas de las distribuciones de probabilidad

Teorema de Bayes

Experimento factorial

Principio de máxima entropía