Prisma hexagonal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Prisma con una base de 6 caras

Uniforme uniforme prisma hexagonal

Tipo	Prismatic uniform polyhedron
Elementos	F = 8, E = 18, V = 12 (χ = 2)
Caras por lados	6{4}+2{6}
Símbolo Schläfli	t{2,6} o {6}×{}
Signatura Wythoff	2 6 Silencio 2 2 2 3 Silencio
Coxeter diagramas
Simmetría	D6h, [6,2], (*622), orden 24
Grupo de rotación	D₆, [6,2]⁺, (622), orden 12
Referencias	U_{76 d)}
Doble	Dipyramid hexagonal
Propiedades	convex, zonohedron
Vertex figure 4.4.6

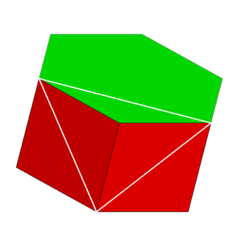
En geometría, el prisma hexagonal es un prisma con base hexagonal. Los prismas son poliedros; este poliedro tiene 8 caras, 18 aristas y 12 vértices.

Como tiene 8 caras, es un octaedro. Sin embargo, el término octaedro se utiliza principalmente para referirse al octaedro regular, que tiene ocho caras triangulares. Debido a la ambigüedad del término octaedro y la tilaridad de las distintas figuras de ocho lados, el término rara vez se utiliza sin aclaración.

Antes de afilarlos, muchos lápices toman la forma de un largo prisma hexagonal.

Como poliedro semirregular (o uniforme)

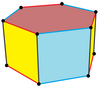
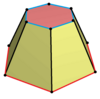
Si todas las caras son regulares, el prisma hexagonal es un poliedro semirregular, más generalmente, un poliedro uniforme, y el cuarto de un conjunto infinito de prismas formados por lados cuadrados y dos extremos de polígonos regulares. Puede verse como un hosoedro hexagonal truncado, representado por el símbolo de Schläfli t{2,6}. Alternativamente, puede verse como el producto cartesiano de un hexágono regular y un segmento de línea, y representado por el producto {6}×{}. El dual de un prisma hexagonal es una bipirámide hexagonal.

El grupo de simetría de un prisma hexagonal recto es D6h de orden 24. El grupo de rotación es D₆ de orden 12.

Volumen

Como en la mayoría de los prismas, el volumen se encuentra tomando el área de la base, con una longitud lateral de ${displaystyle a}$ , y multiplicarlo por la altura ${displaystyle h}$ , dando la fórmula:

${displaystyle V={frac {3{sqrt {3}}}{2}}a^{2}times h}$ y su superficie puede ser ${displaystyle S=3a({sqrt {3}}a+2h)}$ .

Simetría

La topología de un prisma hexagonal uniforme puede tener variaciones geométricas de simetría inferior, que incluyen:

Simmetría	D_6h[2,6], (*622)	C_6v, [6], (*66)	D_3h[2,3], (*322)		D_3d[2]⁺,6], (2*3)
Nombre	El prisma hexagonal regular	frusto hexagonal	Ditrigonal prism	Triambic prism	Ditrigonal trapezoprismo
Construcción	{6}×{},		,		s₂{2,6},
Imagen
Distorsión

Como parte de teselados espaciales

Existe como celdas de cuatro panales prismáticos uniformes y convexos en 3 dimensiones:

Miel prismática hexagonalb	Triangular-hexagonal prismatic honeycomb	Snub triangular-hexagonal prismatic honeycomb	Rhombitriangular-hexagonal prismatic honeycomb

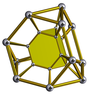
También existe como células de una serie de 4 politopos uniformes de cuatro dimensiones, que incluyen:

truncated tetrahedral prism	prisma octaedral truncado	Prisma cuboctaedral truncado	Prisma icosahedral truncado	Prisma icosidodecedral truncado

de 5 células	Omnitruncado 5 celdas	de 16 celdas	Tesseract omnitrucado

24 celdas	24 celdas	de 600 células	omnitruncada de 120 células

Poliedros y mosaicos relacionados

Uniform hexagonal dihedral spherical polyhedra
Simetría: [6,2], (*622)							[6,2]⁺, (622)	[6,2]⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	S{2,6}
Duals to uniforms

V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Este poliedro puede considerarse miembro de una secuencia de patrones uniformes con figura de vértice (4.6.2p) y diagrama de Coxeter-Dynkin . Para p Los miembros de la secuencia son poliedros omnitruncados (zonohedrones), mostrados a continuación como revestimientos esféricos. Para p Ø 6, son los revestimientos del plano hiperbólico, empezando por el azulejo triheptagonal truncado.

n32 mutación de simetría de los revestimientos omnímicos: 4.6.2n* v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paraco.	Hiperbólico no consumado
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Gráficos
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Contenido relacionado

Más resultados...