Radián

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

El radián, denotado por el símbolo rad, es la unidad SI para medir ángulos y es la unidad estándar de medida angular utilizada en muchas áreas de las matemáticas. La unidad era anteriormente una unidad complementaria del SI (antes de que se aboliera esa categoría en 1995) y el radián es ahora una unidad derivada del SI. El radián se define en el SI como una unidad adimensional con 1 rad = 1. En consecuencia, su símbolo a menudo se omite, especialmente en la escritura matemática.

Definición

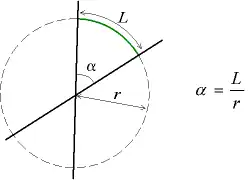
Un radián se define como el ángulo subtendido desde el centro de un círculo que intercepta un arco de longitud igual al radio del círculo. De manera más general, la magnitud en radianes de un ángulo subtendido es igual a la relación entre la longitud del arco y el radio del círculo; es decir, θ = s / r, donde θ es el ángulo subtendido en radianes, s es la longitud del arco y r es el radio. La longitud y el radio del arco pueden tomarse como 1 metro, por lo tanto, 1 radián = 1 m / m. Un cálculo similar usando el área de un sector circular θ = 2 A / r da 1 radian como 1 m/ metro. El hecho clave es que el radián es una unidad adimensional igual a 1. En SI 2019, el radián se define en consecuencia como 1 rad = 1.

En la escritura matemática, el símbolo "rad" a menudo se omite. Cuando se cuantifica un ángulo en ausencia de cualquier símbolo, se asumen radianes, y cuando se quiere decir grados, se usa el signo de grado °.

La magnitud en radianes de una revolución completa (360 grados) es la longitud de toda la circunferencia dividida por el radio, o 2 π r / r, o 2 π. Por lo tanto, 2 π radianes equivalen a 360 grados, lo que significa que un radián equivale a 180/ π grados ≈ 57,29577 95130 82320 876 grados.

La relación 2 π rad = 360° se puede derivar usando la fórmula para la longitud del arco ${displaystyle ell _{text{arc}}=2pi rleft({tfrac {theta }{360^{circ }}}right)}$ , y usando un círculo de radio 1. Dado que el radián es la medida de un ángulo que subtiende un arco de una longitud igual al radio del círculo, ${displaystyle 1=2pi left({tfrac {1{text{rad}}}{360^{circ }}}right)}$ . Esto se puede simplificar aún más a ${displaystyle 1={tfrac {2pi {text{rad}}}{360^{circ }}}}$ . Multiplicar ambos lados por 360° da 360° = 2 π rad.

Historia

Definición de el ángulo de un círculo en un radián

El concepto de medida en radianes, en oposición al grado de un ángulo, normalmente se atribuye a Roger Cotes en 1714. Describió el radián en todo menos en el nombre, y reconoció su naturalidad como unidad de medida angular. Antes de que el término radián se generalizara, la unidad se llamaba comúnmente medida circular de un ángulo.

La idea de medir ángulos por la longitud del arco ya la usaban otros matemáticos. Por ejemplo, al-Kashi (c. 1400) usó las llamadas partes de diámetro como unidades, donde una parte de diámetro era 1/60 radianes. También utilizaron subunidades sexagesimales de la parte del diámetro.

El término radián apareció impreso por primera vez el 5 de junio de 1873, en las preguntas de examen formuladas por James Thomson (hermano de Lord Kelvin) en el Queen's College de Belfast. Había usado el término ya en 1871, mientras que en 1869, Thomas Muir, entonces de la Universidad de St Andrews, vaciló entre los términos rad, radial y radián. En 1874, después de una consulta con James Thomson, Muir adoptó el radian. El nombre radián no fue adoptado universalmente durante algún tiempo después de esto. La trigonometría de la escuela de Longmans todavía se llamaba la medida circular en radianes cuando se publicó en 1890.

Símbolo de la unidad

La Oficina Internacional de Pesos y Medidas y la Organización Internacional de Normalización especifican rad como el símbolo del radián. Los símbolos alternativos utilizados hace 100 años son (la letra c en superíndice, para "medida circular"), la letra r o un superíndice, pero estas variantes se utilizan con poca frecuencia, ya que pueden confundirse con un símbolo de grado (°) o un radio. (R). Por lo tanto, un valor de 1,2 radianes normalmente se escribiría como 1,2 rad; otras notaciones incluyen 1.2 r, 1.2, 1.2 o 1.2.

Conversiones

vueltas	radianes	Grados	Gradianes o gons
0 turno	0 rad	0°	0
1 / 24 vuelta	π / 12 rad	15°	16 + 2 / 3
1 / 16 de vuelta	π / 8 rad	22,5°	25
1 / 12 de vuelta	π / 6 rad	30°	33 + 1 / 3
1 / 10 vuelta	π / 5 rad	36°	40
1/8 de vuelta _	π / 4 rad	45°	50
1 / 2 π vuelta	1 rad	C. 57,3°	C. 63.7
1/6 de vuelta _	π / 3 rad	60°	66 + 2 / 3
1/5 de vuelta _	2 π / 5 rad	72°	80
1/4 de vuelta _	π / 2 rad	90°	100
1/3 de vuelta _	2 π / 3 rad	120°	133 + 1 / 3
2 / 5 de vuelta	4 π / 5 rad	144°	160
1 / 2 vuelta	π rad	180°	200
3/4 de vuelta _	3 π / 2 rad	270°	300
1 turno	2 π rad	360°	400

Conversion entre radianes y grados

Como se dijo, un radián es igual a ${displaystyle {180^{circ }}/{pi }}$ . Por lo tanto, para convertir de radianes a grados, multiplique por ${displaystyle {180^{circ }}/{pi }}$ . ${text{ángulo en grados}}={text{ángulo en radianes}}cdot {frac {180^{circ }}{pi }}$

Por ejemplo: $1{text{ rad}}=1cdot {frac {180^{circ }}{pi }}approx 57,2958^{circ }$ $2,5{text{ rad}}=2,5cdot {frac {180^{circ }}{pi }}aprox. 143,2394^{circ }$ ${frac {pi }{3}}{text{ rad}}={frac {pi }{3}}cdot {frac {180^{circ }}{pi }}=60 ^{ círculo}$

Por el contrario, para convertir de grados a radianes, multiplique por ${displaystyle {pi }/{180^{circ }}}$ . ${text{ángulo en radianes}}={text{ángulo en grados}}cdot {frac {pi }{180^{circ }}}$

Por ejemplo: ${displaystyle 1^{circ }=1^{circ }cdot {frac {pi }{180^{circ }}}approx 0.0175{text{ rad}}}$

{displaystyle 23^{circ }=23^{circ }cdot {frac {pi }{180^{circ }}}approx 0,4014{text{ rad}}}

Los radianes se pueden convertir en vueltas (revoluciones completas) dividiendo el número de radianes por 2 π.

Derivación de conversión de radianes a grados

La longitud de la circunferencia de un círculo viene dada por $2pi r$ , donde $r$ es el radio del círculo.

Entonces la siguiente relación equivalente es verdadera:

${displaystyle 360^{circ }riff 2pi r}$ [Dado $360^{circ}$ que se necesita un barrido para dibujar un círculo completo]

Por la definición de radianes, un círculo completo representa: ${frac{2pi r}{r}}{text{rad}}$ $=2pi {texto{rad}}$

Combinando las dos relaciones anteriores: $2pi {text{rad}}=360^{circ }$ $Rrightarrow 1{text{ rad}}={frac {360^{circ }}{2pi }}$ $Rrightarrow 1{text{ rad}}={frac {180^{circ }}{pi }}$

Conversión entre radianes y gradianes

$2pi$ radianes equivalen a una vuelta, que por definición es 400 gradianes (400 gons o 400). Entonces, para convertir de radianes a gradianes, multiplique por ${displaystyle 200^{text{g}}/pi }$ , y para convertir de gradianes a radianes, multiplique por ${displaystyle pi /200^{text{g}}}$ . Por ejemplo, $1,2{text{ rad}}=1,2cdot {frac {200^{text{g}}}{pi }}aprox. 76,3944^{text{g}}$ ${displaystyle 50^{text{g}}=50^{text{g}}cdot {frac {pi }{200^{text{g}}}}aprox. 0,7854{text{ radical}}}$

Ventajas de medir en radianes

Algunos ángulos comunes medidos en radianes

En cálculo y en la mayoría de las otras ramas de las matemáticas más allá de la geometría práctica, los ángulos se miden universalmente en radianes. Esto se debe a que los radianes tienen una "naturalidad" matemática que conduce a una formulación más elegante de varios resultados importantes.

En particular, los resultados del análisis que implican funciones trigonométricas se pueden expresar con elegancia cuando los argumentos de las funciones se expresan en radianes. Por ejemplo, el uso de radianes conduce a la fórmula de límite simple $lim _{hrightarrow 0}{frac {sin h}{h}}=1,$

que es la base de muchas otras identidades en matemáticas, incluyendo ${frac{d}{dx}}sen x=cos x$ ${frac {d^{2}}{dx^{2}}}sen x=-sen x.$

Debido a estas y otras propiedades, las funciones trigonométricas aparecen en soluciones a problemas matemáticos que no están obviamente relacionados con los significados geométricos de las funciones (por ejemplo, las soluciones a la ecuación diferencial ${displaystyle {tfrac {d^{2}y}{dx^{2}}}=-y}$ , la evaluación de la integral ${ estilo de visualización estilo de texto int { frac {dx} {1 + x ^ {2}}},}$ , etc.). En todos estos casos, se encuentra que los argumentos de las funciones se escriben más naturalmente en la forma que corresponde, en contextos geométricos, a la medida de ángulos en radianes.

Las funciones trigonométricas también tienen expansiones en serie simples y elegantes cuando se usan radianes. Por ejemplo, cuando x está en radianes, la serie de Taylor para sen x se convierte en: $sin x=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7 !}}+cpuntos.$

Si x se expresara en grados, entonces la serie contendría factores desordenados que involucran potencias de π /180: si x es el número de grados, el número de radianes es y = π x / 180, entonces $sin x_{mathrm {grados} }=sin y_{mathrm {rad} }={frac {pi }{180}}x-left({frac {pi }{180}} derecha)^{3} {frac {x^{3}}{3!}}+left({frac {pi }{180}}derecha)^{5} {frac {x ^{5}}{5!}}-left({frac {pi }{180}}right)^{7} {frac {x^{7}}{7!}}+ cdots$

Con un espíritu similar, las relaciones matemáticamente importantes entre las funciones seno y coseno y la función exponencial (ver, por ejemplo, la fórmula de Euler) se pueden enunciar elegantemente, cuando los argumentos de las funciones están en radianes (y desordenados en caso contrario).

Análisis dimensional

SI define los radianes como una unidad adimensional, lo que significa que su dimensión es 1. Al menos una docena de científicos han hecho propuestas para tratar el radián como una unidad de medida base que define su propia dimensión de "ángulo", desde 1936 y tan recientemente como 2022, y la CCU consideró una propuesta para hacer de los radianes una unidad base del SI en 1980. Quincey (2016) considera varias propuestas. Uno de ellos es la propuesta de Torrens de introducir una constante η igual a 1 radián inverso (1 rad), de manera similar a la introducción de la constante ε ₀. Con este cambio, la fórmula para el ángulo subtendido en el centro de un círculo, s = rθ, se modifica para convertirse en s =ηrθ, y la serie de Taylor para el seno de un ángulo θ se convierte en:

{displaystyle operatorname {Sin} theta =sin(eta theta)=eta theta -{frac {(eta theta)^{3}}{3!}}+{frac { (eta theta)^{5}}{5!}}-{frac {(eta theta)^{7}}{7!}}+cdots.}

La función en mayúscula ${displaystyle operatorname {Pecado} }$ toma un argumento con una dimensión de ángulo, mientras que $pecado$ conserva su interpretación habitual como una función sobre números puros. Esta distinción se puede ignorar si las dimensiones son claras por el contexto.

El SI se puede considerar en relación con este marco como un sistema de unidades naturales donde se supone que se cumple la ecuación η = 1, o de manera similar 1 rad = 1. Esta convención de radianes permite la omisión de η en fórmulas matemáticas.

La constante η es "bastante extraña" y es probable que la dificultad de modificar las ecuaciones para agregar η impida su uso generalizado. La CCU rechazó la propuesta de 1980 para evitar un trastorno en la práctica actual. Definir el radián como unidad base puede ser útil para el software, donde la desventaja de las ecuaciones más largas es mínima.

Uso en física

El radián se usa ampliamente en física cuando se requieren mediciones angulares. Por ejemplo, la velocidad angular normalmente se mide en radianes por segundo (rad/s). Una revolución por segundo es igual a 2 π radianes por segundo.

De manera similar, la aceleración angular a menudo se mide en radianes por segundo por segundo (rad/s).

A los efectos del análisis dimensional, las unidades de velocidad angular y aceleración angular son s y s respectivamente.

Asimismo, la diferencia de fase de dos ondas también se puede medir en radianes. Por ejemplo, si la diferencia de fase de dos ondas es (n ⋅2 π) radianes, donde n es un número entero, se consideran en fase, mientras que si la diferencia de fase de dos ondas es (n ⋅2 π + π), donde n es un número entero, se consideran en antifase.

SI múltiplos

Los prefijos métricos para submúltiplos se usan con radianes. Un miliradián (mrad) es una milésima parte de un radián y un microrradián (μrad) es una millonésima parte de un radián, es decir, 1 rad = 10 mrad = 10 μrad.

Hay 2 π × 1000 milirradianes (≈ 6283,185 mrad) en un círculo. Entonces, un miliradián es justo menos de 1/6283 del ángulo subtendido por un círculo completo. Esta unidad "real" de medida angular de un círculo la utilizan los fabricantes de miras telescópicas que utilizan telémetros (estadiamétricos) en retículas. La divergencia de los rayos láser también suele medirse en milirradianes.

La OTAN y otras organizaciones militares utilizan una aproximación del milirradián (0,001 rad) en artillería y selección de objetivos. Cada mil angular representa 1/6400 de un círculo y es 15/8 % o 1,875 % más pequeño que el miliradián. Para los ángulos pequeños que normalmente se encuentran en el trabajo de puntería, la conveniencia de usar el número 6400 en el cálculo supera los pequeños errores matemáticos que introduce. En el pasado, otros sistemas de artillería han utilizado diferentes aproximaciones a 1/2000 π; por ejemplo, Suecia usó el streck 1/6300 y la URSS usó 1/6000 . Al estar basado en el milirradián, el mil de la OTAN subtiende aproximadamente 1 m en un rango de 1000 m (en ángulos tan pequeños, la curvatura es insignificante).

Los prefijos más pequeños que mili son útiles para medir ángulos extremadamente pequeños. Los microrradianes (μrad) y los nanorradianes (nrad) se utilizan en astronomía y también se pueden utilizar para medir la calidad del haz de láseres con divergencia ultrabaja. Más común es el segundo de arco, que es π / 648 000 rad (alrededor de 4,8481 microrradianes).

Contenido relacionado

Más resultados...