Pirámide (geometría)

En geometría, una pirámide (del griego antiguo πυραμίς (puramís)) es un poliedro formado conectando una base poligonal y un punto, llamado vértice. Cada borde de la base y cada vértice forman un triángulo, llamado cara lateral. Es un sólido cónico con base poligonal. Se pueden encontrar muchos tipos de pirámides determinando la forma de las bases o cortando el vértice. Se puede generalizar a una dimensión superior, conocida como hiperpirámide. Todas las pirámides son autoduales.

Definición

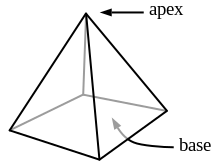
Una pirámide es un poliedro que se puede formar conectando una base poligonal y un punto, llamado vértice. Cada borde de la base y cada vértice forman un triángulo isósceles, llamado cara lateral. Las aristas conectadas desde los vértices de la base poligonal hasta el vértice se denominan aristas laterales. Históricamente, la definición de pirámide ha sido descrita por muchos matemáticos en la antigüedad. Euclides en sus Elementos definió una pirámide como una figura sólida, construida desde un plano hasta un punto. El contexto de su definición era vago hasta que Garza de Alejandría la definió como la figura juntando la punta con una base poligonal.

Un prismatoide se define como un poliedro donde sus vértices se encuentran en dos planos paralelos, sus caras laterales son triángulos, trapecios y paralelogramos. Las pirámides se clasifican en prismatoides.

Clasificación y tipos

La familia de una pirámide base poligonal regular: tetraedro, pirámide cuadrada, pirámide pentagonal, y pirámide hexagonal.

Una pirámide recta es una pirámide donde la base está circunscrita al círculo y la altura de la pirámide se encuentra en el centro del círculo. Esta pirámide se puede clasificar según la regularidad de sus bases. Una pirámide con un polígono regular como base se llama pirámide regular. Para la pirámide con una base regular de n-, tiene n + 1 vértices, n + 1 caras y 2n aristas. Dicha pirámide tiene triángulos isósceles como caras, con su simetría es C_nv, una simetría de orden 2n: las pirámides son simétricas ya que giran alrededor de su eje de simetría (una línea que pasa por el vértice y el centroide de la base) , y son simétricas especulares con respecto a cualquier plano perpendicular que pase por una bisectriz de la base. Algunos ejemplos son la pirámide cuadrada y la pirámide pentagonal, una pirámide de cuatro y cinco caras triangulares con base cuadrada y pentágono, respectivamente; se clasifican como el primer y segundo sólido de Johnson si sus caras y aristas regulares tienen la misma longitud y sus simetrías son C_4v. de orden 8 y C_5v de orden 10, respectivamente. Un tetraedro o pirámide triangular es un ejemplo que tiene cuatro triángulos equiláteros, con todas las aristas de igual longitud, y uno de ellos considerado como base. Debido a que las caras son regulares, es un ejemplo de sólido platónico y deltaedro, y tiene simetría tetraédrica. Una pirámide cuya base es un círculo se conoce como cono. Las pirámides tienen la propiedad de ser autoduales, lo que significa que sus duales son iguales a los vértices correspondientes a las aristas y viceversa. Su esqueleto se puede representar como el gráfico de la rueda.

Pirámides con bases rectangulares y romábicas

Una pirámide recta también puede tener una base con un polígono irregular. Ejemplos de ello son las pirámides con rectángulo y rombo como base. Estas dos pirámides tienen la simetría de C_2v de orden 4.

Una pirámide truncada por un plano inclinado

Una pirámide pentagrama-base.

El tipo de pirámides se puede derivar de muchas maneras. La regularidad de la base de una pirámide se puede clasificar según el tipo de polígono, y un ejemplo es la pirámide con un polígono estrella regular como base, conocida como <span class="anchor" id="Star_pyramid" pirámide estelar. La pirámide cortada por un plano se llama pirámide truncada; Si el plano de truncamiento es paralelo a la base de una pirámide, se llama tronco.

Mensuration

La superficie es el área total de las caras de cada polihedra. En el caso de una pirámide, su superficie es la suma del área de triángulos y el área de la base poligonal.

El volumen de una pirámide es el producto de un tercio del área de la base y la altura. Dado que B{displaystyle B} es el área de la base y h{displaystyle h} es la altura de una pirámide. Matemáticamente, el volumen de una pirámide es:

V=13Bh.{displaystyle V={frac {1}{3}Bh.}

Generalización

La hiperpirámide es la generalización de una pirámide en un espacio n-dimensional. En el caso de la pirámide, se conectan todos los vértices de la base, un polígono en un plano, con un punto fuera del plano, que es la cima. La altura de la pirámide es la distancia del pico al plano. Esta construcción se generaliza a n dimensiones. La base se convierte en un (n − 1)-politopo en un (n − 1)-hiperplano dimensional. Un punto llamado vértice se encuentra fuera del hiperplano y se conecta a todos los vértices del politopo y la distancia del vértice al hiperplano se llama altura.

El volumen n-dimensional de un n-la hiperpirámide dimensional se puede calcular de la siguiente manera:

Vn=A⋅ ⋅ hn.{displaystyle V_{n}={frac {Acdot h} {n}}}