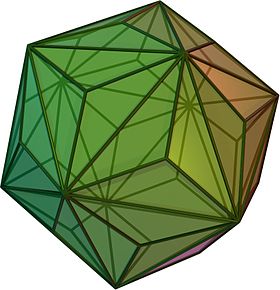
Icosaedro de Triakis

Triakis icosahedron
(Haga clic aquí para el modelo giratorio)
Tipo	Catalán sólido
Coxeter diagrama
Notación de Conway	kI
Tipo de cara	V3.10.10 triángulo isosceles
Caras	60
Edges	90
Vertices	32
Vertices por tipo	20{3}+12{10}
Grupo de simetría	Ih, H3[5,3], (*532)
Grupo de rotación	I, [5,3]+, (532)
Ángulo Dihedral	160°36′45′′ arccos(−24 + 15√5/61)
Propiedades	convex, face-transitive
Truncado dodecaedro (poliedro dual)	Net

En geometría, el icosaedro triakis es un sólido dual de Arquímedes, o sólido catalán, con 60 caras de triángulo isósceles. Su dual es el dodecaedro truncado. También se le ha llamado kisicosaedro. Fue representado por primera vez, en una forma no convexa con caras de triángulos equiláteros, por Leonardo da Vinci en Divina proporcionale de Luca Pacioli, donde recibió el nombre de icosaedro elevatum. La cápside del virus de la hepatitis A tiene la forma de un icosaedro de triakis.

Como un Kleetope

El icosaedro triakis se puede formar pegando pirámides triangulares a cada cara de un icosaedro regular. Dependiendo de la altura de estas pirámides con respecto a su base, el resultado puede ser convexo o no convexo. Esta construcción, de pegar pirámides a cada cara, es un ejemplo de una construcción general llamada Kleetope; el icosaedro triakis es el Kleetope del icosaedro. Esta interpretación también se expresa en el nombre triakis, que se utiliza para los Kleetopes de poliedros con caras triangulares.

Triakis icosahedro no convexo dibujado por Leonardo da Vinci en Luca Pacioli Divina proportione

Las partes visibles de un pequeño triambique icosahedron tienen la misma forma que un triakis no-convexo icosahedron

El gran dodecaedro estelar, con 12 caras pentagrama, tiene un triakis icosahedro como su caparazón exterior

Cuando se representa en la forma de Leonardo, con caras de triángulos equiláteros, es un ejemplo de un deltaedro no convexo, uno de los pocos deltaedros conocidos que son isoédricos (lo que significa que todas las caras son simétricas entre sí). En otra de las formas no convexas del icosaedro triakis, los tres triángulos adyacentes a cada pirámide son coplanares y, en cambio, se puede considerar que forman las partes visibles de un hexágono convexo, en un poliedro que se intersecta a sí mismo con 20 caras hexagonales que ha sido llamado el pequeño icosaedro triámbico. Alternativamente, para la misma forma del icosaedro triakis, las ternas de triángulos isósceles coplanares forman las caras de la primera estelación del icosaedro. Otra forma más, no convexa, con caras de triángulo isósceles dorado, forma la capa exterior del gran dodecaedro estrellado, un poliedro de Kepler-Poinsot con doce caras de pentagrama.

Cada arista del icosaedro triakis tiene extremos de grado total al menos 13. Según el teorema de Kotzig, esto es lo más posible para cualquier poliedro. El mismo grado total se obtiene del Kleetope de cualquier poliedro con grado mínimo cinco, pero el icosaedro triakis es el ejemplo más simple de esta construcción. Aunque este Kleetope tiene caras de triángulo isósceles, la iteración de la construcción de Kleetope produce poliedros convexos con caras triangulares que no pueden ser todas isósceles.

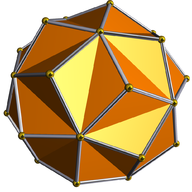
Como sólido catalán

El icosaedro triakis es un sólido catalán, el poliedro dual del dodecaedro truncado. El dodecaedro truncado es un sólido de Arquímedes, con caras que son decágonos regulares y triángulos equiláteros, y con todas las aristas de longitud unitaria; sus vértices se encuentran en una esfera común, la circunsfera del decaedro truncado. La reciprocidad polar de este sólido a través de esta esfera es una forma convexa del icosaedro triakis, con todas las caras tangentes a la misma esfera, ahora una esfera inscrita, con coordenadas y dimensiones que se pueden calcular de la siguiente manera.

Vamos. φ φ {displaystyle varphi } denota la relación de oro. Los bordes cortos de esta forma de los triakis icosahedron tienen longitud

5φ φ +1511. . 2.099{displaystyle {frac {5varphi +15}{11}approx 2.099},

y los bordes largos tienen longitud

φ φ +2. . 3.618{displaystyle varphi +2approx 3.618}.

Sus caras son triángulos isósceles con un ángulo obtuso de

#− − 1⁡ ⁡ − − 3φ φ 10. . 119∘ ∘ {displaystyle cos ^{-1}{frac {-3varphi } {10}approx 119^{circ }

y dos ángulos agudos de

#− − 1⁡ ⁡ φ φ +710. . 30,5∘ ∘ {displaystyle cos ^{-1}{frac {varphi +7}approx 30.5^{circ }.

Como sólido catalán, sus ángulos dihedral son todos iguales, #− − 1⁡ ⁡ φ φ 2()1+2φ φ ()2+φ φ )()1+5φ φ 4)()1+φ φ 2()2+φ φ )2. . {displaystyle cos ^{-1}{frac {varphi ^{2}(1+2varphi (2+varphi)}{sqrt {(1+5varphi ^{4})(1+varphi ^{2}(2+varphi)}}}}}approx }160°36'45.188". Un posible conjunto de 32 coordenadas cartesianas para los vértices de los triakis icosahedron centrados en el origen (escaladas diferente a la anterior) se puede generar combinando los vértices de dos sólidos platónicos adecuadamente escalados, el icosahedro regular y un dodecaedro regular:

• Doce vértices de un icosahedro regular, escalado para tener una unidad circunradius, con las coordenadas
  ()0,± ± 1,± ± φ φ )φ φ 2+1,()± ± 1,± ± φ φ ,0)φ φ 2+1,()± ± φ φ ,0,± ± 1)φ φ 2+1.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}} {fnMicroc {pm 1,varphi0)}{sqrt {varphi ^{2}+1}}}}}}} {frac {h00h00}{f}{f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnMicrocf}f}fnMicrocfnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMin

  
• Veinte vértices de un dodecaedro regular, escalado para tener circunradius
  2+φ φ 3+2φ φ 32− − 1/φ φ =11175+65. . 0.8548,{displaystyle {frac {2+varphi # {3+2varphi}{sqrt {frac {3}{2-1/varphi }={frac {1}{sqrt {75+6{sqrt {5}}}approx 0.8548,}

  
  con las coordenadas
  ()± ± 1,± ± 1,± ± 1)75+65113{displaystyle (pm 1,pm 1,pm 1){frac {sqrt {75+6{sqrt {5}}{11{sqrt {}}}

  
  y
  ()0,± ± φ φ ,± ± 1φ φ )75+65113,()± ± 1φ φ ,0,± ± φ φ )75+65113,()± ± φ φ ,± ± 1φ φ ,0)75+65113.{fnMicrosoft Sans Serif} {fnMicros {}}} {fnMicroc {75+6{sqrt {5}}}}{11{sqrt {3}}}}},(pm {frac {1}{rt}}},0,pmvarphi) {fnMicroc {fnMicroc} {f}}}} {fnMicrocf}}} {f}}}fnMisfnMisfnMisfnMisfnMisfnMisfnMisfnMisfnMis}fnMinMisfnMis}fnMissfnMisfnMinMisfnMinMisfnMisssfnMisfnMinMisfnMinMisfnMinMinMinMinMissfnMinMin {5}}} {11{sqrt {3}}}}} {pm varphipm {frac {1}{varphi }},0){frac {sqrt {75+6{sqrt {5}}{11{sqrt}} {sqrt}}}} {11{sqrt}}}}}}}} {f}} {f} {f}}} {f}}}}}}}}}} {f}}} {f} {f}}} {f}} {f}}}}}} {f} {f}} {f} {f}}}}} {f} {f}}} {f}}}}}}} {f}}} {f} {f} {f} {f}}}}}} {f}}}}}}}}}}}}}}}}}}} {f}}}}}} {3}}}}

  

Simetría

En cualquiera de sus formas estándar convexas o no convexas, el icosaedro triakis tiene las mismas simetrías que un icosaedro regular. Los tres tipos de ejes de simetría del icosaedro, a través de dos vértices opuestos, puntos medios de aristas y centroides de caras, se convierten respectivamente en ejes a través de pares opuestos de vértices de grado diez del icosaedro de triakis, a través de puntos medios opuestos de aristas entre vértices de grado diez, y a través de pares opuestos de vértices de grado tres.