Hexaedro tetrakis

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

sólido catalán con 24 caras

Tetrakis hexahedron
(Haga clic aquí para el modelo giratorio)
Tipo	Catalán sólido
Coxeter diagrama
Notación de Conway	kC
Tipo de cara	V4.6.6 triángulo isosceles
Caras	24
Edges	36
Vertices	14
Vertices por tipo	6{4}+8{6}
Grupo de simetría	Oh, B₃, [4,3], (*432)
Grupo de rotación	O, [4,3]⁺, (432)
Ángulo Dihedral	143°07′48′ arccos(−4/5)
Propiedades	convex, face-transitive
Truncado octaedro (poliedro dual)	Net

Doble compuesto de octaedro truncado y tetrakis hexahedron. El corte de madera a la izquierda es de Perspectiva Corporum Regularium (1568) de Wenzel Jamnitzer.

Modelo de fundición y cristal

Modelo de dibujo y cristal de variante con simetría tetraedral llamada hexakis tetrahedron

En geometría, un hexaedro tetrakis (también conocido como tetrahexaedro, hextetraedro, cubo tetrakis y kiscube) es un sólido catalán. Su dual es el octaedro truncado, un sólido de Arquímedes.

Se le puede llamar hexaedro disdyakis o tetraedro hexakis como el dual de un tetraedro omnitruncado y como la subdivisión baricéntrica de un tetraedro.

Coordenadas cartesianas

Las coordenadas cartesianas de los 14 vértices de un hexaedro tetrakis centrado en el origen, son los puntos

{displaystyle {bigl (}{pm {tfrac {3}{2}}},0,0{bigr)}, {bigl (}0,pm {tfrac {3}{2}},0{bigr)}, {bigl (}0,0,pm {tfrac {3}{2}}{bigr)}, {bigl (}{pm 1},pm 1,pm 1{bigr)}.}

La longitud de los bordes más cortos de este tetrakis hexahedron equivale a 3/2 y la de los bordes más largos equivale a 2. Las caras son triángulos isosceles agudos. El ángulo más grande de estos iguales ${displaystyle arccos {tfrac {1}{9}}approx 83.62^{circ }}$ y los dos más pequeños iguales ${displaystyle arccos {tfrac {2}{3}}approx 48.19^{circ }}$ .

Proyecciones ortogonales

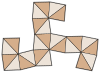
El hexaedro tetrakis, dual del octaedro truncado, tiene 3 posiciones de simetría, dos ubicadas en los vértices y una en el borde medio.

Proyecciones ortogonales
Projective simetría	[2]	[4]	[6]
Tetrakis hexahedron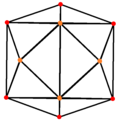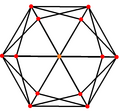
Truncado octaedro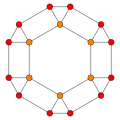

Usos

Se observan formaciones naturales (cristalinas) de tetrahexaedros en sistemas de cobre y fluorita.

Los dados poliedral en forma de tetrakis hexahedron son ocasionalmente utilizados por los jugadores.

Una proyección de 24 celdas vista bajo una proyección en perspectiva de primer vértice tiene una topología de superficie de un hexaedro tetrakis y las proporciones geométricas del dodecaedro rómbico, con las caras rómbicas divididas en dos triángulos.

El hexaedro tetrakis aparece como uno de los ejemplos más simples en la teoría de la construcción. Considere el espacio simétrico de Riemann asociado al grupo SL4(R). Su límite de Tetas tiene la estructura de un edificio esférico cuyos apartamentos son esferas bidimensionales. La partición de esta esfera en simples esféricos (cámaras) se puede obtener tomando la proyección radial de un hexaedro tetrakis.

Simetría

Con simetría tetraédrica T_d, [3,3] (*332), las caras triangulares representan los 24 dominios fundamentales de la simetría tetraédrica. Este poliedro se puede construir a partir de 6 grandes círculos en una esfera. También se puede ver por un cubo con sus caras cuadradas trianguladas por sus vértices y centros de caras y un tetraedro con sus caras divididas por vértices, aristas medias y un punto central.


Truncatedoctahedron	Disdyakis hexahedron	Deltoidaldodecahedron

Rhombichexahedron	Tetraedro

Poliedro esférico

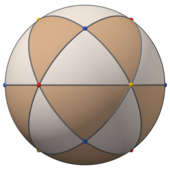(ver modelo giratorio)	Proyecciones ortoográficas de ejes 2, 3 y 4 veces

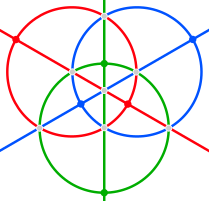
Los bordes del hexaedro tetrakis esférico pertenecen a seis grandes círculos, que corresponden a planos especulares en simetría tetraédrica. Se pueden agrupar en tres pares de círculos ortogonales (que normalmente se cruzan en un eje de coordenadas cada uno). En las imágenes siguientes, estos hosoedros cuadrados están coloreados en rojo, verde y azul.

Proyecciones estereográficas
	2 veces	3 veces	4 veces

Dimensiones

Si denotamos la longitud del borde del cubo base por $a$ , la altura de cada pirámide cumbre sobre el cubo es ${displaystyle {tfrac {a}{4}}.}$ La inclinación de cada cara triangular de la pirámide contra la cara del cubo es ${displaystyle arctan {tfrac {1}{2}}approx 26.565^{circ }}$ (secuencia) A073000 en el OEIS). Un borde de los triángulos isosceles tiene longitud $a$ , los otros dos tienen longitud ${displaystyle {tfrac {3a}{4}},}$ que sigue aplicando el teorema pitagórico a la altura y la longitud base. Esto produce una altitud ${displaystyle {tfrac {{sqrt {5}}a}{4}}}$ en el triángulo (OEIS: A204188). Su área es ${displaystyle {tfrac {{sqrt {5}}a^{2}}{8}},}$ y los ángulos internos son ${displaystyle arccos {tfrac {2}{3}}approx 48.1897^{circ }}$ y complementarios ${displaystyle 180^{circ }-2arccos {tfrac {2}{3}}approx 83.6206^{circ }.}$

El volumen de la pirámide es ${displaystyle {tfrac {a^{3}}{12}};}$ así que el volumen total de las seis pirámides y el cubo en el hexahedron es ${displaystyle {tfrac {3a^{3}}{2}}.}$

Kleetope

Puede verse como un cubo con pirámides cuadradas que cubren cada cara cuadrada; es decir, es el Kleetope del cubo. Una forma no convexa de esta forma, con caras de triángulos equiláteros, tiene la misma geometría de superficie que el octaedro regular, y un modelo de octaedro de papel se puede volver a doblar para darle esta forma. Esta forma del hexaedro tetrakis fue ilustrada por Leonardo da Vinci en Divina proporcionale de Luca Pacioli (1509).

Esta forma no convexa del hexaedro tetrakis se puede plegar a lo largo de las caras cuadradas del cubo interior como una red para una pirámide cúbica de cuatro dimensiones.

Polimedros y poliedros relacionados

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]⁺ (432)	[1]⁺,4,3] = [3,3] (*332)		[3]⁺4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1.1}	t{3,4} t{3^1.1}	{3,4} {3}^1.1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{3^1.1}

		=	=	=				= o	= o	=

Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

*n32 mutación simetría de los revestimientos truncados: n.6.6 v t e
Sym. *n42 [n,3]	Spherical				Euclid.	Compacto		Parac.	Hiperbólico no consumado
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncado cifras
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	JUEGO.6	12i.6.6	9i.6.6	6i.6.6
N-kis cifras
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V dieta.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Es un polihedra en una secuencia definida por la configuración facial V4.6.2n. Este grupo es especial para tener todo el número de bordes por vértice y formar planos de bisección a través de la polihedra y líneas infinitas en el plano, y continuar en el plano hiperbólico para cualquier n ≥ 7.

Con un número par de caras en cada vértice, estos poliedros y mosaicos se pueden mostrar alternando dos colores para que todas las caras adyacentes tengan colores diferentes.

Cada cara en estos dominios también corresponde al dominio fundamental de un grupo de simetría con orden 2,3,n espejos en cada vértice de la cara del triángulo.

n32 mutación de simetría de los revestimientos omnímicos: 4.6.2n* v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paraco.	Hiperbólico no consumado
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Gráficos
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Contenido relacionado

Más resultados...