Error de tipo I y de tipo II

Los errores de tipo I y de tipo II son equivocaciones metodológicas durante la prueba de hipótesis nulas que invierten el resultado correcto. En el ámbito de las pruebas de hipótesis estadísticas, es fundamental comprender los conceptos de error de tipo I y error de tipo II pues estos son piedras angulares del estudio y la aplicación de la metodología estadística, especialmente en campos como la medicina, la biometría y la informática.

El error de tipo I, comúnmente conocido como 'falso positivo', ocurre cuando se rechaza incorrectamente una hipótesis nula que en realidad es verdadera. Este tipo de error es análogo a condenar a una persona inocente en un contexto judicial. La minimización de los errores de tipo I es crucial en la investigación estadística, aunque su eliminación total es estadísticamente imposible. Para reducir la probabilidad de cometer este error, los investigadores ajustan el valor del umbral de significancia, conocido como nivel alfa (p).

Por otro lado, el error de tipo II, o 'falso negativo', se produce cuando se acepta erróneamente una hipótesis nula falsa. Este error es equivalente a no condenar a una persona culpable. La gravedad de un error de tipo II varía según el contexto y depende del tamaño y la dirección del efecto no detectado. Por ejemplo, en un estudio médico, pasar por alto una cura efectiva para una enfermedad rara podría tener consecuencias significativas, aunque la enfermedad afecte a una minoría.

Intuitivamente, los errores de tipo I pueden verse como errores de comisión, donde se concluye erróneamente que existe un efecto o relación. Por ejemplo, en un estudio clínico, si un medicamento parece efectivo debido al azar en comparación con un placebo, se estaría cometiendo un error de tipo I al considerar el medicamento eficaz. En contraste, los errores de tipo II son errores de omisión, donde se falla en detectar un efecto real. Siguiendo el mismo ejemplo, si el medicamento es efectivo pero el estudio no logra demostrarlo, se estaría frente a un error de tipo II.

La comprensión y gestión de estos errores son esenciales para la integridad de la investigación estadística. Aunque es imposible eliminarlos completamente, el conocimiento y la correcta aplicación de técnicas estadísticas minimizan su impacto, llevando a conclusiones suficientemente fiables y válidas para la investigación científica.

Error de Tipo I: El Falso Positivo

El error de Tipo I, comúnmente conocido como falso positivo, se produce en el contexto de las pruebas de hipótesis estadísticas. Este error ocurre cuando una hipótesis nula, que es en realidad verdadera, es rechazada incorrectamente como resultado de un procedimiento de prueba. En otras palabras, se presenta cuando los resultados de un análisis sugieren la existencia de un efecto o una diferencia que, en realidad, no existe.

Este tipo de error es una de las preocupaciones más significativas en el campo de la estadística y la investigación científica, ya que puede llevar a conclusiones erróneas y, en algunos casos, a decisiones basadas en evidencia falsa. La probabilidad de cometer un error de Tipo I en una prueba se denota comúnmente como alfa (α), y este valor es establecido por el investigador antes de realizar la prueba. Un valor alfa típico es 0.05, lo que implica que hay un 5% de probabilidad de rechazar la hipótesis nula cuando en realidad es cierta.

En términos más ilustrativos, el error de Tipo I puede ser comparado con un escenario en una sala de audiencias donde un acusado inocente es condenado. En este contexto, la hipótesis nula sería que el acusado es inocente, y el rechazo de esta hipótesis nula se traduce en una condena errónea.

Este paralelismo ayuda a entender la gravedad de un error de Tipo I, ya que conlleva afirmar la presencia de algo que no existe, como la culpabilidad de una persona inocente. Por lo tanto, en la investigación científica, se pone especial cuidado en la elección del nivel de significancia para minimizar la posibilidad de cometer este tipo de error, aunque nunca se puede eliminar por completo. La conciencia y comprensión de este error son cruciales para garantizar la fiabilidad y la integridad de los resultados obtenidos en cualquier estudio estadístico.

Error de Tipo II: El Falso Negativo

El error de Tipo II, conocido también como falso negativo, representa una situación en la que, durante el proceso de prueba de hipótesis estadísticas, se acepta erróneamente una hipótesis nula que en realidad es falsa. Este tipo de error ocurre cuando los datos de un estudio no son suficientemente convincentes para demostrar un efecto real, llevando a la conclusión equivocada de que no hay diferencia o relación cuando en realidad sí existe.

La probabilidad de cometer un error de Tipo II se denota como beta (β), y está inversamente relacionada con el poder estadístico del estudio. Un alto poder estadístico significa una menor probabilidad de cometer un error de Tipo II. Este error es especialmente crítico en campos como la investigación médica y farmacéutica, donde pasar por alto un efecto verdadero puede tener consecuencias graves, como no reconocer la eficacia de un nuevo tratamiento.

Para ilustrar este concepto en un contexto más tangible, podemos compararlo con un escenario en una sala de audiencias donde un criminal es absuelto. En este caso, la hipótesis nula sería que el acusado no ha cometido el crimen, y aceptar erróneamente esta hipótesis nula equivaldría a dejar en libertad a un criminal. Este paralelismo destaca la seriedad de un error de Tipo II en la investigación estadística, ya que implica no detectar una diferencia o relación significativa.

Por ejemplo, en un estudio clínico, podría significar no reconocer los beneficios de un medicamento que realmente es efectivo. Por lo tanto, es crucial para los investigadores diseñar sus estudios de manera que se minimice la probabilidad de este tipo de error, aumentando el tamaño de la muestra o utilizando técnicas estadísticas más sensibles, para garantizar que los resultados sean lo más precisos y fiables posible.

HSD

Definiciones

Antecedentes estadísticos

En la teoría de la prueba estadística, la noción de un error estadístico es una parte integral de la prueba de hipótesis. La prueba consiste en elegir entre dos proposiciones en competencia llamadas hipótesis nula, denotada por H ₀ e hipótesis alternativa, denotada por H ₁. Esto es conceptualmente similar a la sentencia en un juicio judicial. La hipótesis nula corresponde a la posición del imputado: así como se presume su inocencia hasta que se pruebe su culpabilidad, la hipótesis nula se presume verdadera hasta que los datos aporten pruebas fehacientes en su contra. La hipótesis alternativa corresponde a la posición contra el demandado. Específicamente, la hipótesis nula también implica la ausencia de una diferencia o la ausencia de una asociación. Por lo tanto, la hipótesis nula nunca puede ser que exista una diferencia o una asociación.

Si el resultado de la prueba se corresponde con la realidad, entonces se ha tomado una decisión correcta. Sin embargo, si el resultado de la prueba no se corresponde con la realidad, entonces se ha producido un error. Hay dos situaciones en las que la decisión es incorrecta. La hipótesis nula puede ser verdadera, mientras que rechazamos H ₀. Por otro lado, la hipótesis alternativa H ₁ puede ser verdadera, mientras que no rechazamos H ₀. Se distinguen dos tipos de error: error de tipo I y error de tipo II.

Tasa de error cruzado

La tasa de error cruzado (CER) es el punto en el que los errores de tipo I y los errores de tipo II son iguales y representa la mejor forma de medir la eficacia de la biometría. Un sistema con un valor CER más bajo proporciona más precisión que un sistema con un valor CER más alto.

Falso positivo y falso negativo

En cuanto a los falsos positivos y falsos negativos, un resultado positivo corresponde a rechazar la hipótesis nula, mientras que un resultado negativo corresponde a no rechazar la hipótesis nula; "falso" significa que la conclusión extraída es incorrecta. Así, un error de tipo I equivale a un falso positivo y un error de tipo II equivale a un falso negativo.

Tabla de tipos de errores

Relaciones tabularizadas entre verdad/falsedad de la hipótesis nula y resultados de la prueba:

Tabla de tipos de errores	La hipótesis nula ( H 0 ) es
Cierto	Falso
Decisión sobre la hipótesis nula ( H 0 )	no rechaces	Inferencia correcta (verdadero negativo)(probabilidad = 1− α )	Error tipo II (falso negativo) (probabilidad = β )
Rechazar	Error tipo I (falso positivo) (probabilidad = α )	Inferencia correcta (verdadero positivo)(probabilidad = 1− β )

Tasa de error

Una prueba perfecta tendría cero falsos positivos y cero falsos negativos. Sin embargo, los métodos estadísticos son probabilísticos y no se puede saber con certeza si las conclusiones estadísticas son correctas. Siempre que hay incertidumbre, existe la posibilidad de cometer un error. Teniendo en cuenta esta naturaleza de la ciencia estadística, todas las pruebas de hipótesis estadísticas tienen una probabilidad de cometer errores de tipo I y tipo II.

• La tasa de error tipo I o nivel de significación es la probabilidad de rechazar la hipótesis nula dado que es cierta. Se denota con la letra griega α (alfa) y también se le llama nivel alfa. Por lo general, el nivel de significación se establece en 0,05 (5 %), lo que implica que es aceptable tener una probabilidad del 5 % de rechazar incorrectamente la hipótesis nula verdadera.
• La tasa del error de tipo II se denota con la letra griega β (beta) y se relaciona con la potencia de una prueba, que es igual a 1−β.

Estos dos tipos de tasas de error se compensan entre sí: para cualquier conjunto de muestras dado, el esfuerzo por reducir un tipo de error generalmente da como resultado un aumento del otro tipo de error.

La calidad de la prueba de hipótesis.

La misma idea puede expresarse en términos de la tasa de resultados correctos y, por lo tanto, usarse para minimizar las tasas de error y mejorar la calidad de la prueba de hipótesis. Para reducir la probabilidad de cometer un error de Tipo I, hacer que el valor alfa (p) sea más estricto es bastante simple y eficiente. Para disminuir la probabilidad de cometer un error de tipo II, que está estrechamente relacionado con la potencia de los análisis, aumentar el tamaño de la muestra de la prueba o relajar el nivel alfa podría aumentar la potencia de los análisis. Una estadística de prueba es robusta si se controla la tasa de error de tipo I.

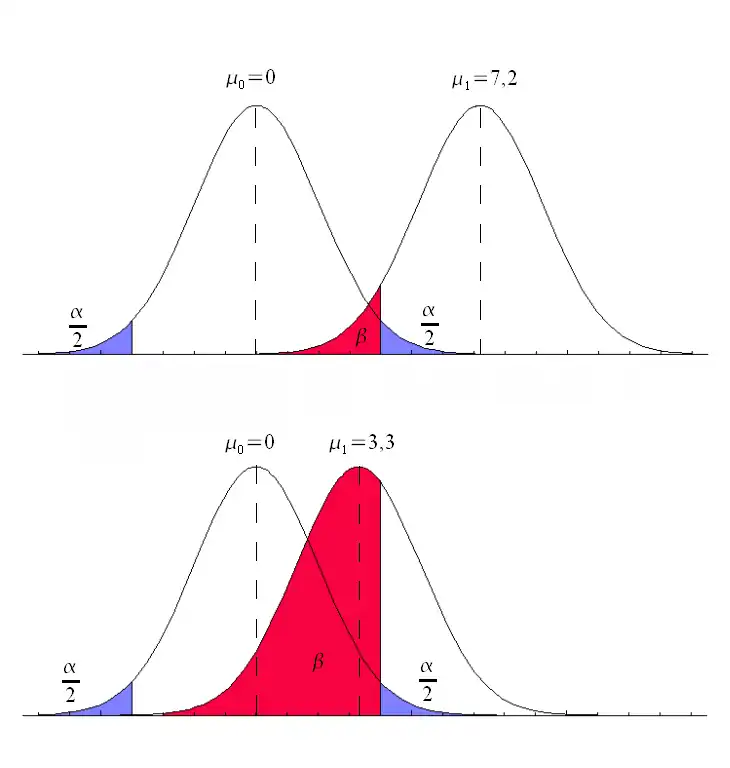
También se podría utilizar un valor de umbral (límite) diferente para hacer que la prueba sea más específica o más sensible, lo que a su vez eleva la calidad de la prueba. Por ejemplo, imagine una prueba médica, en la que el experimentador podría medir la concentración de cierta proteína en la muestra de sangre. El experimentador podría ajustar el umbral (línea vertical negra en la figura) y se diagnosticaría a las personas con enfermedades si se detecta un número por encima de este umbral determinado. Según la imagen, cambiar el umbral daría como resultado cambios en falsos positivos y falsos negativos, correspondientes al movimiento en la curva.

Ejemplo

Dado que en un experimento real es imposible evitar todos los errores de tipo I y tipo II, es importante considerar la cantidad de riesgo que uno está dispuesto a correr para rechazar H ₀ o aceptar H ₀ falsamente. La solución a esta pregunta sería reportar el valor p o nivel de significancia α de la estadística. Por ejemplo, si el valor p del resultado de una estadística de prueba se estima en 0,0596, entonces hay una probabilidad del 5,96 % de que rechacemos falsamente H ₀. O, si decimos que la estadística se realiza en el nivel α, como 0.05, entonces permitimos rechazar falsamente H ₀ al 5%. Un nivel de significación α de 0,05 es relativamente común, pero no existe una regla general que se ajuste a todos los escenarios.

Medición de la velocidad del vehículo

El límite de velocidad de una autopista en los Estados Unidos es de 120 kilómetros por hora. Se configura un dispositivo para medir la velocidad de los vehículos que pasan. Suponga que el dispositivo realizará tres mediciones de la velocidad de un vehículo que pasa, registrando como una muestra aleatoria X ₁, X ₂, X ₃. La policía de tránsito multará o no a los conductores dependiendo de la velocidad promedio . Es decir, el estadístico de prueba

Además, suponemos que las medidas X ₁, X ₂, X ₃ se modelan como una distribución normal N(μ,4). Entonces, T debería seguir a N(μ,4/3) y el parámetro μ representa la verdadera velocidad del vehículo que pasa. En este experimento, la hipótesis nula H ₀ y la hipótesis alternativa H ₁ deben ser

H ₀: μ=120 contra H ₁: μ ₁ >120.

Si realizamos el nivel estadístico en α=0.05, entonces se debe calcular un valor crítico c para resolver

Según la regla del cambio de unidades para la distribución normal. Con referencia a la tabla Z, podemos obtener

Aquí, la región crítica. Es decir, si la velocidad registrada de un vehículo es superior al valor crítico 121,9, el conductor será multado. Sin embargo, todavía hay un 5% de los conductores que son multados falsamente ya que la velocidad media registrada es superior a 121,9 pero la velocidad real no pasa de 120, lo que decimos, un error tipo I.

El error tipo II corresponde al caso de que la velocidad real de un vehículo supere los 120 kilómetros por hora y no se multe al conductor. Por ejemplo, si la velocidad real de un vehículo μ=125, la probabilidad de que el conductor no sea multado se puede calcular como

<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4a1af1b5ac244b82f88e47bd6e0e725d0b2c8cb7" alt="{\displaystyle P=(T<121.9|\mu =125)=P\left({\frac {T-125}{\frac {2}{\sqrt {3}}}}

lo que significa que si la velocidad real de un vehículo es 125, la conducción tiene una probabilidad del 0,36 % de evitar la multa cuando la estadística se realiza en el nivel 125, ya que la velocidad media registrada es inferior a 121,9. Si la velocidad real está más cerca de 121,9 que de 125, entonces la probabilidad de evitar la multa también será mayor.

También se deben considerar las compensaciones entre el error de tipo I y el error de tipo II. Es decir, en este caso, si la policía de tránsito no quiere multar falsamente a conductores inocentes, el nivel α se puede establecer en un valor menor, como 0.01. Sin embargo, si ese es el caso, más conductores cuya velocidad real es superior a 120 kilómetros por hora, como 125, tendrían más probabilidades de evitar la multa.

Etimología

En 1928, Jerzy Neyman (1894-1981) y Egon Pearson (1895-1980), ambos eminentes estadísticos, discutieron los problemas asociados con "decidir si una muestra en particular puede o no ser juzgada como probable de haber sido extraída al azar de una determinada población". ": y, como señaló Florence Nightingale David, "es necesario recordar que el adjetivo 'aleatorio' [en el término 'muestra aleatoria'] debe aplicarse al método de extracción de la muestra y no a la muestra en sí".

Identificaron "dos fuentes de error", a saber:(a) el error de rechazar una hipótesis que no debería haber sido rechazada, y(b) el error de no rechazar una hipótesis que debería haber sido rechazada.

En 1930, desarrollaron estas dos fuentes de error y señalaron que:

... al probar hipótesis se deben tener en cuenta dos consideraciones, debemos ser capaces de reducir la posibilidad de rechazar una hipótesis verdadera a un valor tan bajo como se desee; la prueba debe diseñarse de tal manera que rechace la hipótesis probada cuando es probable que sea falsa.

En 1933, observaron que estos "problemas rara vez se presentan de tal forma que podamos discriminar con certeza entre la hipótesis verdadera y la falsa". También señalaron que, al decidir si fallar en rechazar o rechazar una hipótesis particular entre un "conjunto de hipótesis alternativas", H ₁, H ₂..., era fácil cometer un error:

...[y] estos errores serán de dos tipos:
(I) rechazamos H ₀ [es decir, la hipótesis a probar] cuando es verdadera,(II) no podemos rechazar H ₀ cuando alguna hipótesis alternativa H _A o H ₁ es verdadera. (Hay varias notaciones para la alternativa).

En todos los artículos coescritos por Neyman y Pearson, la expresión H ₀ siempre significa "la hipótesis a probar".

En el mismo trabajo denominan a estas dos fuentes de error errores de tipo I y errores de tipo II respectivamente.

Términos relacionados

Hipótesis nula

Es una práctica habitual que los estadísticos realicen pruebas para determinar si una " hipótesis especulativa " relativa a los fenómenos observados del mundo (o de sus habitantes) puede sustentarse o no. Los resultados de tales pruebas determinan si un conjunto particular de resultados concuerda razonablemente (o no concuerda) con la hipótesis especulada.

Sobre la base de que siempre se asume, por convención estadística, que la hipótesis especulada es incorrecta, y la llamada " hipótesis nula " de que los fenómenos observados ocurren simplemente por casualidad (y que, como consecuencia, el agente especulado no tiene efecto) – la prueba determinará si esta hipótesis es correcta o incorrecta. Esta es la razón por la cual la hipótesis bajo prueba a menudo se llama hipótesis nula (probablemente, acuñada por Fisher (1935, p. 19)), porque es esta hipótesis la que debe ser anulada o no anulada por la prueba. Cuando se anula la hipótesis nula, es posible concluir que los datos apoyan la " hipótesis alternativa ".(que es el especulado original).

La aplicación consistente por parte de los estadísticos de la convención de Neyman y Pearson de representar " la hipótesis a probar " (o " la hipótesis a ser anulada ") con la expresión H ₀ ha llevado a circunstancias en las que muchos entienden el término " la hipótesis nula " en el sentido de " la hipótesis nula ": una declaración de que los resultados en cuestión han surgido por casualidad. Este no es necesariamente el caso: la restricción clave, según Fisher (1966), es que " la hipótesis nula debe ser exacta, es decir, libre de vaguedad y ambigüedad, porque debe proporcionar la base del 'problema de distribución'". de los cuales la prueba de significación es la solución. "Como consecuencia de esto, en la ciencia experimental la hipótesis nula es generalmente una declaración de que un tratamiento particular no tiene efecto; en la ciencia observacional, es que no hay diferencia entre el valor de una variable medida en particular y el de una predicción experimental.

Significancia estadística

Si la probabilidad de obtener un resultado tan extremo como el obtenido, suponiendo que la hipótesis nula fuera cierta, es menor que una probabilidad de corte preestablecida (por ejemplo, 5%), entonces se dice que el resultado es estadísticamente significativo. y se rechaza la hipótesis nula.

El estadístico británico Sir Ronald Aylmer Fisher (1890-1962) enfatizó que la "hipótesis nula":

... nunca se prueba o establece, pero posiblemente se desaprueba, en el curso de la experimentación. Puede decirse que todo experimento existe sólo para dar a los hechos la oportunidad de refutar la hipótesis nula.—  Fisher, 1935, pág. 19

Dominios de aplicación

Medicamento

En la práctica de la medicina, las diferencias entre las aplicaciones de detección y prueba son considerables.

Exámenes médicos

La detección implica pruebas relativamente baratas que se administran a grandes poblaciones, ninguna de las cuales manifiesta ninguna indicación clínica de enfermedad (p. ej., pruebas de Papanicolaou).

Las pruebas implican procedimientos mucho más costosos, a menudo invasivos, que se administran solo a quienes manifiestan alguna indicación clínica de enfermedad y, con mayor frecuencia, se aplican para confirmar un diagnóstico sospechoso.

Por ejemplo, la mayoría de los estados de EE. UU. exigen que los recién nacidos se sometan a pruebas de detección de fenilcetonuria e hipotiroidismo, entre otros trastornos congénitos.

Hipótesis: “Los recién nacidos tienen fenilcetonuria e hipotiroidismo”

Hipótesis Nula (H ₀ ): “Los recién nacidos no tienen fenilcetonuria e hipotiroidismo,”

Error tipo I (falso positivo): Lo cierto es que los recién nacidos no tienen fenilcetonuria e hipotiroidismo pero consideramos que tienen los trastornos según los datos.

Error tipo II (falso negativo): Lo cierto es que los recién nacidos tienen fenilcetonuria e hipotiroidismo pero consideramos que no tienen los trastornos según los datos.

Aunque muestran una alta tasa de falsos positivos, las pruebas de detección se consideran valiosas porque aumentan en gran medida la probabilidad de detectar estos trastornos en una etapa mucho más temprana.

Los análisis de sangre simples que se utilizan para detectar el VIH y la hepatitis en los posibles donantes de sangre tienen una tasa significativa de falsos positivos; sin embargo, los médicos utilizan pruebas mucho más costosas y precisas para determinar si una persona está realmente infectada con alguno de estos virus.

Quizás los falsos positivos más discutidos en la detección médica provienen de la mamografía del procedimiento de detección del cáncer de mama. La tasa de mamografías con falsos positivos en EE. UU. es de hasta un 15 %, la más alta del mundo. Una consecuencia de la alta tasa de falsos positivos en los EE. UU. es que, en cualquier período de 10 años, la mitad de las mujeres estadounidenses examinadas reciben una mamografía de falso positivo. Las mamografías positivas falsas son costosas, con más de $100 millones gastados anualmente en los EE. UU. en pruebas de seguimiento y tratamiento. También causan ansiedad innecesaria a las mujeres. Como resultado de la alta tasa de falsos positivos en los EE. UU., entre el 90 y el 95 % de las mujeres que obtienen un resultado positivo en la mamografía no tienen la afección. La tasa más baja del mundo está en Holanda, 1%.

La prueba de detección de población ideal sería económica, fácil de administrar y, si fuera posible, no produciría falsos negativos. Tales pruebas generalmente producen más falsos positivos, que posteriormente pueden resolverse mediante pruebas más sofisticadas (y costosas).

Pruebas médicas

Los falsos negativos y los falsos positivos son problemas importantes en las pruebas médicas.

Hipótesis: “Los pacientes tienen la enfermedad específica”.

Hipótesis nula (H ₀ ): “Los pacientes no tienen la enfermedad específica”.

Error tipo I (falso positivo): “El hecho real es que los pacientes no tienen una enfermedad específica, pero los médicos juzgan que los pacientes estaban enfermos de acuerdo con los informes de las pruebas”.

Los falsos positivos también pueden producir problemas graves y contradictorios cuando la afección que se busca es rara, como en la detección. Si una prueba tiene una tasa de falsos positivos de uno en diez mil, pero solo una en un millón de muestras (o personas) es un verdadero positivo, la mayoría de los positivos detectados por esa prueba serán falsos. La probabilidad de que un resultado positivo observado sea un falso positivo puede calcularse utilizando el teorema de Bayes.

Error de tipo II (falso negativo): "El hecho real es que la enfermedad está realmente presente, pero los informes de las pruebas brindan un mensaje falsamente tranquilizador a los pacientes y médicos de que la enfermedad está ausente".

Los falsos negativos producen problemas serios y contrarios a la intuición, especialmente cuando la condición que se busca es común. Si se usa una prueba con una tasa de falsos negativos de solo el 10 % para probar una población con una tasa de ocurrencia real del 70 %, muchos de los negativos detectados por la prueba serán falsos.

Esto a veces conduce a un tratamiento inapropiado o inadecuado tanto del paciente como de su enfermedad. Un ejemplo común es confiar en las pruebas de esfuerzo cardíaco para detectar la aterosclerosis coronaria, aunque se sabe que las pruebas de esfuerzo cardíaco solo detectan las limitaciones del flujo sanguíneo de las arterias coronarias debido a la estenosis avanzada.

Biometría

La coincidencia biométrica, como la del reconocimiento de huellas dactilares, el reconocimiento facial o el reconocimiento del iris, es susceptible de errores de tipo I y tipo II.

Hipótesis: “La entrada no identifica a alguien en la lista de personas buscadas”

Hipótesis nula: "La entrada identifica a alguien en la lista de personas buscadas"

Error tipo I (tasa de rechazo falso): “El hecho real es que la persona es alguien en la lista buscada pero el sistema concluye que la persona no está de acuerdo con los datos”.

Error tipo II (tasa de coincidencia falsa): “El hecho real es que la persona no es alguien en la lista buscada, pero el sistema concluye que la persona es alguien a quien estamos buscando de acuerdo con los datos”.

La probabilidad de errores de tipo I se denomina "tasa de rechazo falso" (FRR) o tasa de no coincidencia falsa (FNMR), mientras que la probabilidad de errores de tipo II se denomina "tasa de aceptación falsa" (FAR) o tasa de coincidencia falsa ( RMF).

Si el sistema está diseñado para emparejar sospechosos en raras ocasiones, entonces la probabilidad de errores de tipo II puede denominarse "tasa de falsas alarmas". Por otro lado, si el sistema se utiliza para la validación (y la aceptación es la norma), entonces la FAR es una medida de la seguridad del sistema, mientras que la FRR mide el nivel de inconveniencia del usuario.

Control de seguridad

Los falsos positivos se encuentran rutinariamente todos los días en los controles de seguridad de los aeropuertos, que en última instancia son sistemas de inspección visual. Las alarmas de seguridad instaladas están destinadas a evitar que se suban armas a las aeronaves; sin embargo, a menudo se configuran con una sensibilidad tan alta que emiten una alarma muchas veces al día para artículos menores, como llaves, hebillas de cinturones, monedas sueltas, teléfonos móviles y tachuelas en los zapatos.

Aquí, la hipótesis es: “El objeto es un arma”.

La hipótesis nula: “El objeto no es un arma”.

Error de tipo I (falso positivo): “El hecho real es que el elemento no es un arma, pero el sistema sigue alarmando”.

Error de tipo II (falso negativo) "El hecho real es que el elemento es un arma, pero el sistema se mantiene en silencio en este momento".

La proporción de falsos positivos (identificar a un viajero inocente como terrorista) a verdaderos positivos (detectar a un posible terrorista) es, por lo tanto, muy alta; y debido a que casi todas las alarmas son falsos positivos, el valor predictivo positivo de estas pruebas de detección es muy bajo.

El costo relativo de los resultados falsos determina la probabilidad de que los creadores de las pruebas permitan que ocurran estos eventos. Dado que el costo de un falso negativo en este escenario es extremadamente alto (no detectar una bomba que se lleva a un avión podría resultar en cientos de muertes), mientras que el costo de un falso positivo es relativamente bajo (una inspección adicional razonablemente simple), el más apropiado es una prueba con una especificidad estadística baja pero una sensibilidad estadística alta (una que permite una alta tasa de falsos positivos a cambio de un mínimo de falsos negativos).

Ordenadores

Las nociones de falsos positivos y falsos negativos tienen una amplia vigencia en el ámbito de las computadoras y las aplicaciones informáticas, incluida la seguridad informática, el filtrado de spam, el malware, el reconocimiento óptico de caracteres y muchos otros.

Por ejemplo, en el caso del filtrado de spam, la hipótesis aquí es que el mensaje es spam.

Por lo tanto, hipótesis nula: “El mensaje no es spam”.

Error de tipo I (falso positivo): "Las técnicas de filtrado o bloqueo de spam clasifican erróneamente un mensaje de correo electrónico legítimo como spam y, como resultado, interfieren con su entrega".

Si bien la mayoría de las tácticas antispam pueden bloquear o filtrar un alto porcentaje de correos electrónicos no deseados, hacerlo sin generar resultados falsos positivos significativos es una tarea mucho más exigente.

Error de tipo II (falso negativo): “El correo electrónico no deseado no se detecta como correo no deseado, pero se clasifica como no deseado”. Un bajo número de falsos negativos es un indicador de la eficiencia del filtrado de spam.