Codominio (matemáticas)

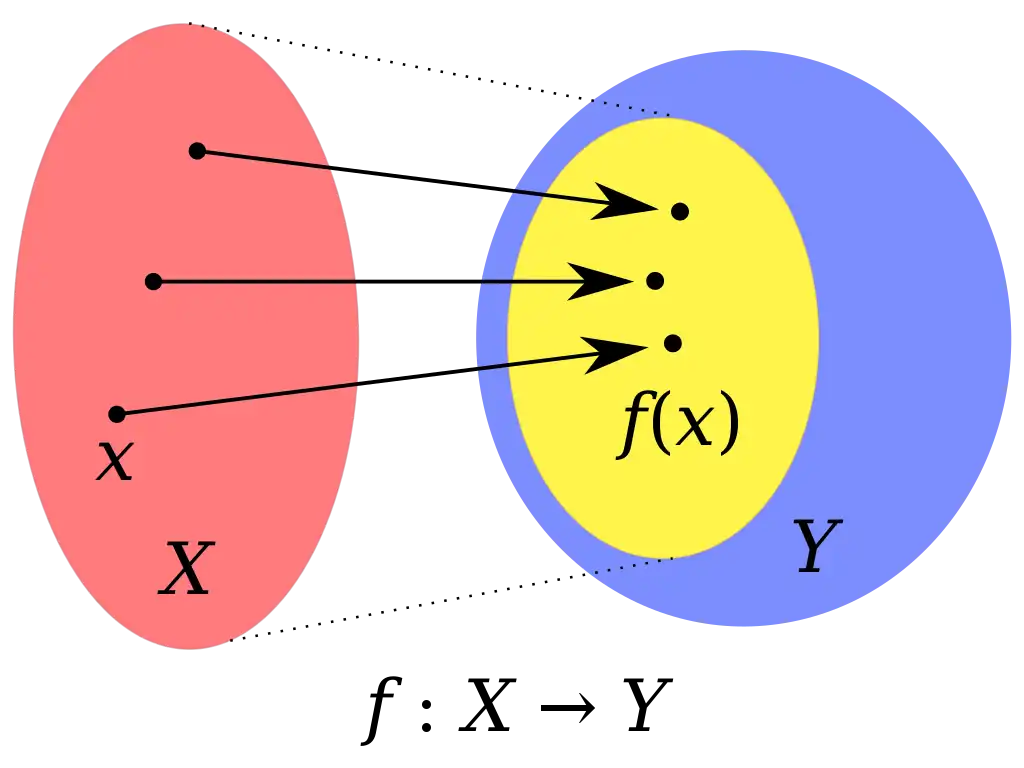
El codominio de una función es el conjunto al que pertenece cualquier valor de salida de la función. En otras palabras, el codominio de una función es la clase de valores salientes (no los resultados) y se denota como Cod (f), Cod f o simplemente Codom (f).

Es importante diferenciar el codominio de una función, de la imagen o rango de una función, ya que ambos términos se parecen, pero no son lo mismo. La imagen de una función se refiere al conjunto de todos los resultados obtenidos al aplicar la función a un dominio. Así, el rango para f(x), es el conjunto de todos los valores que devuelva f(x).

El codominio por su parte, es el conjunto donde podrán encontrarse dichos valores. Así, si f(x) siempre devuelve un número entero R, el codominio será R y dentro de R estará la imágen para f(x). La imagen es entonces un subconjunto del codominio, o el mismo codominio cuando la función es sobreyectiva, pero nunca podría ser mayor al codominio.

La notación de codominio es

f: X → Y

Donde f simboliza la función, X el dominio y Y el codominio de la función

Los codominios son un componente esencial en el estudio de las funciones matemáticas, porque proporcionan un marco para entender dónde se situarán los posibles resultados de una función, y excluir a priori otros elementos.

Diferencia entre codominio y rango (imágen)

El codominio de una función representa todos los posibles valores que antes de aplicarse la función pueden contener la salida que la función. Este conjunto es conocido y establecido en el momento en que se formula la función. Por ejemplo, en la función f(x) = x², donde f: R → R, el codominio es el conjunto de todos los números reales R. Aquí, el codominio incluye todos los números reales porque así se ha definido la función, independientemente de si todos esos valores son realmente producidos por la función o no.

Por esto se denomina también contradominio al codominio, pues no es otra cosa que el dominio donde se alojan los valores del resultado de la función.

En contraste, el rango o imagen de una función es el conjunto de valores que la función efectivamente produce o alcanza cuando opera sobre su dominio. Siguiendo con el mismo ejemplo, aunque el codominio de f(x) = x² es todo R, su imagen es solamente el conjunto de números reales no negativos. Esto se debe a que, al elevar al cuadrado cualquier número real, el resultado nunca puede ser negativo. Por lo tanto, aunque el codominio incluye todos los números reales, la imagen de esta función específica se limita a los números no negativos, demostrando que la imagen es un subconjunto del codominio.

La distinción entre codominio e imagen es crucial para el análisis matemático de funciones. El codominio es una parte integral de la definición de la función y establece el marco teórico para los posibles resultados. Por otro lado, la imagen es un reflejo de la operación real de la función y depende de los valores con los que trabaja. Esta diferencia es especialmente importante en conceptos como las funciones "suprayectivas", en donde una función se considera suprayectiva si su imagen coincide exactamente con su codominio, lo que significa que cada elemento del codominio es el resultado de aplicar la función a algún elemento de su dominio. Entender estas diferencias ayuda a comprender más profundamente cómo funcionan las funciones matemáticas y su comportamiento en diversos contextos.

HSD

Ejemplos

Para una función

f:: R→ → R{displaystyle fcolon mathbb {R} rightarrow mathbb {R}

definido por

f:: x↦ ↦ x2,{displaystyle fcolon ,xmapsto x^{2} o equivalente f()x)=x2,{displaystyle f(x) = x^{2}

el codominio de f es R{displaystyle textstyle mathbb {R}, pero f no mapea a ningún número negativo.
Así la imagen de f es el conjunto R0+{displaystyle textstyle mathbb [R] _{0} {cH00}; es decir, el intervalo [0, ∞].

Una función alternativa g se define así:

g:: R→ → R0+{displaystyle gcolon mathbb {R} rightarrow mathbb [R] _{0} {cH00}

g:: x↦ ↦ x2.{displaystyle gcolon ,xmapsto x^{2}

Mientras f y g asigne un x dado al mismo número, no son, en esta vista, la misma función porque tienen diferentes codominios. Se puede definir una tercera función h para demostrar por qué:

h:: x↦ ↦ x.{displaystyle hcolon ,xmapsto {sqrt {x}}}

El dominio de h no puede ser R{displaystyle textstyle mathbb {R} pero se puede definir R0+{displaystyle textstyle mathbb [R] _{0} {cH00}:

h:: R0+→ → R.{displaystyle hcolon mathbb {R} _{0}}derecho mathbb {R}

Las composiciones se denotan

h∘ ∘ f,{displaystyle hcirc f,}

h∘ ∘ g.{displaystyle hcirc g.}

En inspección, h ∘ f no es útil. Es verdad, a menos que se defina otra cosa, que la imagen f no se conoce; sólo se sabe que es un subconjunto de R{displaystyle textstyle mathbb {R}. Por esta razón, es posible que h, cuando se compone con f, podría recibir un argumento para el cual no se define la salida – números negativos no son elementos del dominio h, que es la función de la raíz cuadrada.

Por lo tanto, la composición de funciones es una noción útil solo cuando el codominio de la función en el lado derecho de una composición (no su imagen, que es una consecuencia de la función y podría ser desconocido a nivel de la composición) es un subconjunto del dominio de la función del lado izquierdo.

El codominio afecta si una función es sobreyectiva, en el sentido de que la función es sobreyectiva si y solo si su codominio es igual a su imagen. En el ejemplo, g es una sobreyección, mientras que f no lo es. El codominio no afecta si una función es una inyección.

Un segundo ejemplo de la diferencia entre el codominio y la imagen se demuestra por las transformaciones lineales entre dos espacios vectoriales - en particular, todas las transformaciones lineales de R2{displaystyle textstyle mathbb {R} } {2} a sí mismo, que puede ser representado por 2×2 matrices con coeficientes reales. Cada matriz representa un mapa con el dominio R2{displaystyle textstyle mathbb {R} } {2} y codomain R2{displaystyle textstyle mathbb {R} } {2}. Sin embargo, la imagen es incierta. Algunas transformaciones pueden tener imagen igual a todo el codomain (en este caso las matrices con rango 2) pero muchos no, en lugar de mapear en un subespacio más pequeño (las matrices con rango 1 o 0). Tome por ejemplo la matriz T dado por

T=()1010){displaystyle T={begin{pmatrix}1 ventaja01}}

que representa una transformación lineal que mapea el punto ()x, Sí.) a ()x, x). El punto (2, 3) no está en la imagen de T, pero todavía está en el codominio desde transformaciones lineales de R2{displaystyle textstyle mathbb {R} } {2} a R2{displaystyle textstyle mathbb {R} } {2} son de relevancia explícita. Como todos 2×2 matrices, T representa a un miembro de ese conjunto. Examinar las diferencias entre la imagen y el codominio a menudo puede ser útil para descubrir propiedades de la función en cuestión. Por ejemplo, puede concluirse que T no tiene rango completo ya que su imagen es más pequeña que todo el codomain.