Bloqueo (estadísticas)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Diseño de experimentos para recopilar contextos similares juntos

En la teoría estadística del diseño de experimentos, bloqueo es la disposición de unidades experimentales similares entre sí en grupos (bloques) en función de una o más variables. Estas variables se eligen cuidadosamente para minimizar el impacto de su variabilidad en los resultados observados. Hay diferentes formas de implementar el bloqueo, lo que produce diferentes efectos de confusión. Sin embargo, los diferentes métodos comparten el mismo propósito: controlar la variabilidad introducida por factores específicos que podrían influir en el resultado de un experimento. Las raíces del bloqueo se originaron en el estadístico Ronald Fisher, tras su desarrollo de ANOVA.

Historia

El uso del bloqueo en el diseño experimental tiene una historia en evolución que abarca múltiples disciplinas. Los conceptos fundamentales de bloqueo se remontan a principios del siglo XX con estadísticos como Ronald A. Fisher. Su trabajo en el desarrollo del análisis de varianza (ANOVA) sentó las bases para agrupar unidades experimentales para controlar variables extrañas. El bloqueo evolucionó a lo largo de los años, lo que llevó a la formalización de diseños de bloques aleatorios y diseños de cuadrado latino. Hoy en día, el bloqueo todavía desempeña un papel fundamental en el diseño experimental y, en los últimos años, los avances en el software estadístico y las capacidades computacionales han permitido a los investigadores explorar temas más complejos. diseños de bloqueo.

Usar

El bloqueo reduce la variabilidad inexplicable. Su principio radica en el hecho de que la variabilidad que no se puede superar (por ejemplo, la necesidad de dos lotes de materia prima para producir 1 contenedor de una sustancia química) se confunde o se asocia con una interacción (de orden superior/más alto) para eliminar su influencia en la Producto final. Las interacciones de alto orden suelen ser las de menor importancia (piense en el hecho de que la temperatura de un reactor o del lote de materias primas es más importante que la combinación de ambas; esto es especialmente cierto cuando hay más (3, 4,...) factores están presentes); por tanto, es preferible confundir esta variabilidad con la interacción mayor.

Ejemplos

Hombre y mujer: Un experimento está diseñado para probar un nuevo fármaco en pacientes. Hay dos niveles de tratamiento, drogas, y placebo, administrado a Hombre y hembra pacientes en un ensayo doble ciego. El sexo del paciente es un bloqueo la variabilidad del tratamiento entre hombres y mujeres. Esto reduce las fuentes de variabilidad y conduce a una mayor precisión.
Elevación: Un experimento está diseñado para probar los efectos de un nuevo plaguicida en un parche específico de hierba. El área de césped contiene un cambio de elevación importante y por lo tanto consta de dos regiones distintas – 'alta elevación' y 'baja elevación'. Un grupo de tratamiento (el nuevo plaguicida) y un grupo de placebo se aplican tanto a las zonas de alta elevación como a baja altitud de la hierba. En este caso, el investigador está bloqueando el factor de elevación que puede dar cuenta de variabilidad en la aplicación del plaguicida.
Intervención: Supongamos que se inventa un proceso que pretende hacer que las suelas de los zapatos duren más tiempo, y se forma un plan para llevar a cabo un ensayo de campo. Dado un grupo de n voluntarios, un posible diseño sería dar n/2 de ellos zapatos con las nuevas plantas y n/2 de ellos zapatos con las suelas ordinarias, aleatorizando la asignación de los dos tipos de suelas. Este tipo de experimento es un diseño completamente aleatorizado. A continuación, se pide a ambos grupos que usen sus zapatos durante un período de tiempo, y luego midan el grado de desgaste de las plantas. Este es un diseño experimental viable, pero puramente desde el punto de vista de la exactitud estadística (ignorando cualquier otro factor), un mejor diseño sería dar a cada persona una suela regular y una suela nueva, asignando al azar los dos tipos al zapato izquierdo y derecho de cada voluntario. Tal diseño se llama un "diseño de bloque completo aleatorio". Este diseño será más sensible que el primero, porque cada persona está actuando como su propio control y por lo tanto el grupo de control está más cerca del diseño del grupo de tratamiento

Variables de ruido

En los ejemplos mencionados anteriormente, una variable de molestia es una variable que no es el enfoque primario del estudio, pero puede afectar los resultados del experimento. Se consideran posibles fuentes de variabilidad que, si no son controladas o contabilizadas, pueden confundir la interpretación entre las variables independientes y dependientes.

Para abordar las variables molestas, los investigadores pueden emplear diferentes métodos, como el bloqueo o la aleatorización. El bloqueo implica agrupar unidades experimentales según los niveles de la variable molesta para controlar su influencia. La aleatorización ayuda a distribuir los efectos de las variables molestas de manera uniforme entre los grupos de tratamiento.

Mediante el uso de uno de estos métodos para contabilizar las variables de molestia, los investigadores pueden mejorar la validez interna de sus experimentos, asegurando que los efectos observados sean más probables atribuibles a las variables manipuladas y no a las influencias extraneosas.

En el primer ejemplo proporcionado anteriormente, el sexo del paciente sería una variable molesta. Por ejemplo, considere si el medicamento fuera una pastilla para adelgazar y los investigadores quisieran probar el efecto de las pastillas para adelgazar sobre la pérdida de peso. La variable explicativa es la pastilla para adelgazar y la variable respuesta es la cantidad de peso perdido. Aunque el sexo del paciente no es el foco principal del experimento (el efecto del fármaco sí lo es), es posible que el sexo del individuo afecte la cantidad de peso perdido.

Bloqueo utilizado para factores molestos que se pueden controlar

En la teoría estadística del diseño de experimentos, el bloqueo es la disposición de unidades experimentales en grupos (bloques) que son similares entre sí. Normalmente, un factor de bloqueo es una fuente de variabilidad que no es de interés principal para el experimentador.

Al estudiar la teoría de la probabilidad, el método de bloques consiste en dividir una muestra en bloques (grupos) separados por subbloques más pequeños de modo que los bloques puedan considerarse casi independientes. El método de bloques ayuda a demostrar teoremas de límites en el caso de variables aleatorias dependientes.

El método de los bloques fue introducido por S. Bernstein: El método se aplicó con éxito en la teoría de sumas de variables aleatorias dependientes y en la teoría de valores extremos.

Ejemplo

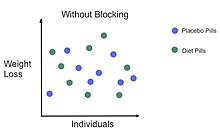
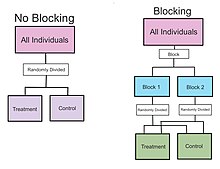
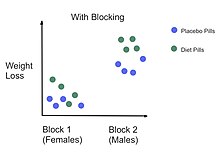
En nuestro ejemplo anterior de pastillas para adelgazar, un factor de bloqueo podría ser el sexo del paciente. Podríamos colocar a los individuos en uno de dos bloques (hombres o mujeres). Y dentro de cada uno de los dos bloques, podemos asignar aleatoriamente a los pacientes a la pastilla de dieta (tratamiento) o a la pastilla de placebo (control). Al bloquear el sexo, se controla esta fuente de variabilidad, lo que lleva a una mayor interpretación de cómo las pastillas para adelgazar afectan la pérdida de peso.

Definición de factores de bloqueo

Un factor de molestia se utiliza como factor de bloqueo si cada nivel del factor primario ocurre el mismo número de veces con cada nivel del factor de molestia. El análisis del experimento se centrará en el efecto de los distintos niveles del factor primario dentro de cada bloque del experimento.

Bloquee algunos de los factores molestos más importantes

La regla general es:

"Bloquea lo que puedas; aleatoriza lo que no puedes."

El bloqueo se utiliza para eliminar los efectos de algunas de las variables molestas más importantes. Luego se utiliza la aleatorización para reducir los efectos contaminantes de las variables molestas restantes. Para variables molestas importantes, el bloqueo producirá una mayor significancia en las variables de interés que la aleatorización.

Implementación

La implementación del bloqueo en el diseño experimental implica una serie de pasos para controlar eficazmente las variables extrañas y mejorar la precisión de las estimaciones del efecto del tratamiento.

Identificar variables molestas

Identificar factores potenciales que no son el enfoque principal del estudio pero que podrían introducir variabilidad.

Seleccione los factores de bloqueo apropiados

Elija cuidadosamente los factores de bloqueo en función de su relevancia para el estudio, así como de su potencial para confundir los principales factores de interés.

Definir tamaños de bloque

Dividir un experimento de cierto tamaño en una cierta cantidad de bloques tiene consecuencias, ya que la cantidad de bloques determina la cantidad de efectos de confusión.

Asignar tratamientos a bloques

Puede optar por asignar aleatoriamente unidades experimentales a las condiciones de tratamiento dentro de cada bloque, lo que puede ayudar a garantizar que cualquier variabilidad no contabilizada se distribuya uniformemente entre los grupos de tratamiento. Sin embargo, dependiendo de cómo asigne los tratamientos a los bloques, puede obtener una cantidad diferente de efectos confusos. Por lo tanto, se puede elegir el número y los efectos específicos que se confunden, lo que significa que asignar tratamientos a bloques es superior a la asignación aleatoria.

Replicación

Al ejecutar un diseño diferente para cada réplica, donde un efecto diferente se confunde cada vez, los efectos de interacción se confunden parcialmente en lugar de sacrificar por completo un solo efecto. La replicación mejora la confiabilidad de los resultados y permite una evaluación más sólida de los efectos del tratamiento.

Ejemplo

Tabla

Una forma útil de ver un experimento de bloques aleatorios es considerarlo como una colección de experimentos completamente aleatorios, cada uno de los cuales se ejecuta dentro de uno de los bloques del experimento total.

Diseños de bloques aleatorios (RBD)
Nombre del diseño	Número de factores k	Número de carreras n
2-factor RBD	2	L₁ * L₂
3-factor RBD	3	L₁ * L₂ * L₃
4-factor RBD	4	L₁ * L₂ * L₃ * L₄
${displaystyle vdots }$	${displaystyle vdots }$	${displaystyle vdots }$
k-factor RBD	k	L₁ * L₂ * ${displaystyle cdots }$ * L_k

con

L₁ = número de niveles (ajustes) del factor 1

L₂ = número de niveles (ajustes) del factor 2

L₃ = número de niveles (ajustes) del factor 3

L₄ = número de niveles (ajustes) del factor 4

{displaystyle vdots }

L_k = número de niveles (ajustes) de factor k

Ejemplo

Supongamos que los ingenieros de una instalación de fabricación de semiconductores quieren probar si diferentes dosis de material para implantes de obleas tienen un efecto significativo en las mediciones de resistividad después de un proceso de difusión que tiene lugar en un horno. Tienen cuatro dosis diferentes que quieren probar y suficientes obleas experimentales del mismo lote para procesar tres obleas en cada una de las dosis.

El factor molesto que les preocupa es el "funcionamiento del horno" ya que se sabe que cada funcionamiento del horno difiere del anterior e impacta muchos parámetros del proceso.

Una forma ideal de ejecutar este experimento sería ejecutar todas las obleas 4x3=12 en el mismo horno. Esto eliminaría por completo el molesto factor del horno. Sin embargo, las obleas de producción regular tienen prioridad en el horno, y solo se permiten unas pocas obleas experimentales en cualquier horno al mismo tiempo.

Una forma no bloqueada de ejecutar este experimento sería ejecutar cada una de las doce obleas experimentales, en orden aleatorio, una por ejecución del horno. Eso aumentaría el error experimental de cada medición de resistividad por la variabilidad del horno entre ejecuciones y haría más difícil estudiar los efectos de las diferentes dosis. La forma bloqueada de ejecutar este experimento, suponiendo que pueda convencer a la fabricación para que le permita colocar cuatro obleas experimentales en un horno, sería colocar cuatro obleas con diferentes dosis en cada una de las tres ejecuciones del horno. La única aleatorización sería elegir cuál de las tres obleas con la dosis 1 entraría en el horno 1, y lo mismo para las obleas con las dosis 2, 3 y 4.

Descripción del experimento

Sea X₁ el "nivel" y X₂ sea el factor de bloqueo del funcionamiento del horno. Entonces el experimento se puede describir de la siguiente manera:

k = 2 factores (1 factor primario X₁ y 1 factor de bloqueo X₂)

L₁ = 4 niveles de factor X₁

L₂ = 3 niveles de factor X₂

n = 1 réplica por celda

N = L₁ * L₂ = 4 * 3 = 12 carreras

Antes de la aleatorización, los ensayos de diseño se ven así:

X₁	X₂
1	1
1	2
1	3
2	1
2	2
2	3
3	1
3	2
3	3
4	1
4	2
4	3

Representación matricial

Una forma alternativa de resumir las pruebas de diseño sería utilizar una matriz de 4x3 cuyas 4 filas sean los niveles del tratamiento X₁ y cuyas columnas sean los 3 niveles de la variable de bloqueo X₂. Las celdas de la matriz tienen índices que coinciden con las combinaciones X₁, X₂ anteriores.

Tratamiento	Bloqueo 1	Bloque 2	Bloque 3
1	1	1	1
2	1	1	1
3	1	1	1
4	1	1	1

Por extensión, tenga en cuenta que las pruebas para cualquier diseño de bloques aleatorios de factor K son simplemente los índices de celda de una matriz dimensional k.

Modelo

El modelo para un diseño de bloques aleatorios con una variable molesta es

{displaystyle Y_{ij}=mu +T_{i}+B_{j}+mathrm {random error} }

Donde

Y_ij es cualquier observación para la cual X₁ = i y X₂ = j

X₁ es el factor primario

X₂ es el factor de bloqueo

μ es el parámetro de ubicación general (es decir, la media)

T_i es el efecto de estar en tratamiento i (del factor X₁)

B_j es el efecto de estar en bloque j (del factor X₂)

Estimaciones

Estimación μ:

{displaystyle {overline {Y}}}

= el promedio de todos los datos

Estimación T_i:

{displaystyle {overline {Y}}_{icdot }-{overline {Y}}}

con

{displaystyle {overline {Y}}_{icdot }}

= promedio de todos Y para la cual X₁ = i.

Estimación B_j:

{displaystyle {overline {Y}}_{cdot j}-{overline {Y}}}

con

{displaystyle {overline {Y}}_{cdot j}}

= promedio de todos Y para la cual X₂ = j.

Generalizaciones

Los diseños de bloques aleatorizados generalizados (GRBD) permiten pruebas de interacción bloque-tratamiento, y tiene exactamente un factor de bloqueo como el RCBD.
Los cuadrados latinos (y otros diseños de columnas) tienen dos factores de bloqueo que se cree que no tienen interacción.
muestreo hipercubo latino
Plazas Graeco-Latin
Diseños cuadrados Hyper-Graeco-Latin

Contenido relacionado

Más resultados...