Argumento de la diagonal de Cantor

Ajustar Compartir Imprimir Citar

Una ilustración del argumento diagonal de Cantor (en base 2) para la existencia de conjuntos incontables. La secuencia en el fondo no puede ocurrir en ningún lugar en la enumeración de secuencias arriba.

Un conjunto infinito puede tener la misma cardinalidad como un subconjunto adecuado de sí mismo, como la bijeción representada f()x)=2x de lo natural a los números incluso lo demuestra. Sin embargo, existen conjuntos infinitos de diferentes cardenalidades, como muestra el argumento diagonal de Cantor.

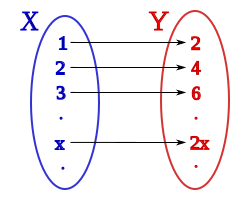
En la teoría de conjuntos, el argumento de la diagonal de Cantor, también llamado argumento de la diagonalización, el argumento de la barra diagonal, el argumento anti-diagonal, el método diagonal y la prueba de diagonalización de Cantor, fue publicado en 1891 por Georg Cantor como prueba matemática de que son conjuntos infinitos que no se pueden poner en correspondencia biunívoca con el conjunto infinito de los números naturales. Tales conjuntos ahora se conocen como conjuntos incontables, y el tamaño de los conjuntos infinitos ahora se trata en la teoría de los números cardinales que comenzó Cantor.

El argumento de la diagonal no fue la primera prueba de Cantor de la incontabilidad de los números reales, que apareció en 1874. Sin embargo, demuestra una técnica general que desde entonces se ha utilizado en una amplia gama de demostraciones, incluido el primero de los teoremas de incompletitud de Gödel y la respuesta de Turing al Entscheidungsproblem. Los argumentos de diagonalización también son a menudo la fuente de contradicciones como la paradoja de Russell y la paradoja de Richard.

Conjunto incontable

Cantor consideró el conjunto T de todas las secuencias infinitas de dígitos binarios (es decir, cada dígito es cero o uno). Comienza con una demostración constructiva del siguiente lema:

Si s₁, s₂,... s_n,... es cualquier enumeración de elementos de T, entonces un elemento s de T se puede construir que no corresponda a ninguna s_n en la enumeración.

La prueba comienza con una enumeración de elementos de T, por ejemplo

s₁ =	(0,	0,	0,	0,	0,	0,	0,	...)
s₂ =	(1,	1,	1,	1,	1,	1,	1,	...)
s₃ =	(0,	1,	0,	1,	0,	1,	0,	...)
s₄ =	(1,	0,	1,	0,	1,	0,	1,	...)
s₅ =	(1,	1,	0,	1,	0,	1,	1,	...)
s₆ =	(0,	0,	1,	1,	0,	1,	1,	...)
s₇ =	(1,	0,	0,	0,	1,	0,	0,	...)
...

A continuación, se construye una secuencia s eligiendo el primer dígito como complementario al primer dígito de s_{1 (cambiando 0s por 1s y viceversa), el segundo dígito como complementario al segundo dígito de s_{< i>2}, el 3er dígito como complementario al 3er dígito de s₃, y en general para cada n, el dígito n^th como complementario al dígito n^th de < i>s_n. Para el ejemplo anterior, esto produce}

s₁	=	()0,	0,	0,	0,	0,	0,	0,	...)
s₂	=	(1,	1,	1,	1,	1,	1,	1,	...)
s₃	=	(0,	1,	0,	1,	0,	1,	0,	...)
s₄	=	(1,	0,	1,	0,	1,	0,	1,	...)
s₅	=	(1,	1,	0,	1,	0,	1,	1,	...)
s₆	=	(0,	0,	1,	1,	0,	1,	1,	...)
s₇	=	(1,	0,	0,	0,	1,	0,	0,	...)
...

s	=	()1,	0,	1,	1,	1,	0,	1,	...)

Por construcción, s es un miembro de T que difiere de cada s_{n< /sub>, ya que sus n^th dígitos difieren (resaltados en el ejemplo).
Por lo tanto, s no puede aparecer en la enumeración.}

Con base en este lema, Cantor usa una prueba por contradicción para mostrar que:

El set T es incontable.

La demostración comienza asumiendo que T es contable. Entonces todos sus elementos se pueden escribir en una enumeración s₁, s₂,... s_n,.... La aplicación del lema anterior a esta enumeración produce una secuencia s que es miembro de T, pero no está en la enumeración. Sin embargo, si se enumera T, entonces todos los miembros de T, incluido este s, están en la enumeración. Esta contradicción implica que la suposición original es falsa. Por lo tanto, T es incontable.

Números reales

La incontableidad de los números reales ya fue establecida por la primera prueba de incontable de Cantor, pero también sigue del resultado anterior. Para probarlo, se construirá una inyección desde el conjunto T de infinitas cuerdas binarias al conjunto R de números reales. Desde T es incontable, la imagen de esta función, que es un subconjunto de REs incontable. Por lo tanto, R es incontable. Además, mediante un método de construcción diseñado por Cantor, se construirá una bijección entre T y R. Por lo tanto, T y R tienen la misma cardenalidad, que se llama la "cardialidad del continuum" y es generalmente denotado por ${displaystyle {Mathfrak}}$ o ${displaystyle 2^{aleph - Sí.$ .

Se proporciona una inyección de T a R mediante la asignación de cadenas binarias en T a fracciones decimales, como la asignación de t = 0111... al decimal 0,0111.... Esta función, definida por f (t) = 0.t, es una inyección porque asigna cadenas diferentes a números diferentes.

Construir una biyección entre T y R es un poco más complicado. En lugar de asignar 0111... al decimal 0,0111..., se puede asignar al número base b: 0,0111..._b. Esto conduce a la familia de funciones: f_b (t) = 0.t_b. Las funciones f _b(t ) son inyecciones, excepto f ₂ (t). Esta función se modificará para producir una biyección entre T y R.

Construcción de una bijección entre T y R
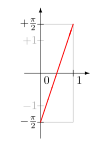
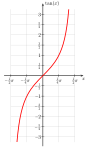
La función h: (0,1) → (π/2,π/2) La función tan: (−π/2,π/2) → R Esta construcción utiliza un método ideado por Cantor que fue publicado en 1878. Lo usó para construir una bijeción entre el intervalo cerrado [0, 1] y los irracionales en el intervalo abierto (0, 1). Primero quitó un subconjunto contablemente infinito de cada uno de estos conjuntos para que haya una bijeción entre los conjuntos incontables restantes. Ya que hay una bijeción entre los subconjuntos contablemente infinitos que se han eliminado, combinando las dos bijeciones produce una bijeción entre los conjuntos originales. El método de Cantor se puede utilizar para modificar la función f₂()t) = 0.t₂ para producir una bijeción de T a (0, 1). Porque algunos números tienen dos expansiones binarias, f₂()t) Ni siquiera es inyectable. Por ejemplo, f₂(1000...) = 0.1000...₂= 1/2 y f₂(0111...) = 0.0111...₂= 1/4 + 1/8 + 1/16 +... = 1/2, así que ambos 1000... y 0111... mapa al mismo número, 1/2. Para modificar f₂()t), observar que es una bijeción excepto por un subconjunto contablemente infinito de (0, 1) y un subconjunto contablemente infinito T. No es una bijeción para los números en (0, 1) que tienen dos expansiones binarias. Estos son llamados números dyadic y tienen la forma m/2ⁿ Donde m es un extraño entero y n es un número natural. Pon estos números en la secuencia: r= (1/2, 1/4, 3/4, 1/8, 3/8, 5/8, 7/8,...). También, f₂()t) no es una bijeción a (0, 1) para las cuerdas en T apareciendo después del punto binario en las expansiones binarias de 0, 1, y los números en secuencia r. Poner estas cadenas eventualmente constantes en la secuencia: s=000... 111..., 1000...111... 01000...111...000..., 10111...,...). Definir la bijeción g()t) de T a (0, 1): Si t es n^T cadena en secuencia s, vamos g()t) ser el n^T número en secuencia r; de lo contrario, g()t) = 0.t₂. Para construir una bijeción de T a R, empezar con la función tangente tan(x), que es una bijección de (−/2, π/2) a R (ver la figura mostrada a la derecha). Siguiente observa que la función lineal h()x) πx – π/2 es una bijeción de (0, 1) a (−π/2, π/2) (ver la figura mostrada en la izquierda). La función compuesta tan(h()x) = tan(π)x – π/2) es una bijeción de (0, 1) a R. Componiendo esta función con g()t) produce la función tan(h()g()t) = tan(π)g()t) – π/2), que es una bijeción de T a R.

Conjuntos generales

Ilustración del argumento diagonal generalizado: El set T =n▪

{displaystyle mathbb {N}

: n∉f()n)} en la parte inferior no puede ocurrir en cualquier lugar en el rango de f:

{displaystyle mathbb {N}

→P(

{displaystyle mathbb {N}

). El mapeo de ejemplo f se corresponde con la enumeración del ejemplo s en la imagen anterior.

Cantor usó una forma generalizada del argumento diagonal para probar el teorema de Cantor: para cada conjunto S, el conjunto potencia de S, es decir, el conjunto de todos los subconjuntos de S (aquí escrito como P(S))—no puede estar en biyección con S mismo. Esta prueba procede de la siguiente manera:

Sea f cualquier función de S a P(S). Basta probar que f no puede ser sobreyectiva. Eso significa que algún miembro T de P(S), es decir, algún subconjunto de S, no está en la imagen de f. Como candidato considere el conjunto:

T = s ▪ S: s ∉ f()s}.

Por cada s en S, s está en T o no. Si s está en T, entonces por definición de T, s no está en f(s), por lo que T no es igual a f(s). Por otro lado, si s no está en T, entonces por definición de T, s está en < i>f(s), de nuevo T no es igual a f(s); cf. imagen. Para una descripción más completa de esta demostración, consulte el teorema de Cantor.

Consecuencias

Ordenación de cardenales

Cantor define una relación de orden de cardenalidades, por ejemplo. ${displaystyle Silencioso$ y ${displaystyle Silencioso$ , en términos de la existencia de inyecciones entre los conjuntos subyacentes, ${displaystyle S.$ y ${displaystyle T}$ . El argumento en el párrafo anterior demostró entonces que se establece como ${displaystyle {Mathbb {N}to {0,1}$ son incontables, lo que es decir ${displaystyle neg (responsable{mathbb {N}to{0,1}tuvoleq Silencio{mathbb {N}$ , y podemos incrustar los naturales en el espacio de la función, para que tengamos eso ${fnMicrosoft Sans Serif} {fnh}\fnh}to\\top,1}\\\\\\\\\\\fnMicrosoft}$ . En el contexto de las matemáticas clásicas, esto agota las posibilidades y el argumento diagonal se puede utilizar para establecer que, por ejemplo, aunque ambos conjuntos bajo consideración son infinitos, en realidad hay más infinitas secuencias de unos y ceros que los números naturales. El resultado de Cantor entonces también implica que la noción del conjunto de todos los conjuntos es inconsistente: Si S eran el conjunto de todos los conjuntos, entonces P()S) sería al mismo tiempo más grande que S y un subconjunto S.

Asumiendo la ley del tercero excluido, todo conjunto subcontable (una propiedad en términos de sobreyecciones) también es contable.

En matemáticas constructivas, es más difícil o imposible ordenar ordinals y también cardenales. Por ejemplo, el teorema Schröder-Bernstein requiere la ley del medio excluido. Por lo tanto, los intuitionistas no aceptan el teorema sobre el orden cardenal. El orden en los reales (el orden estándar que extiende el de los números racionales) tampoco es necesariamente decidable. Tampoco son la mayoría de las propiedades de clases interesantes de funciones decidables, por el teorema de Rice, es decir, el conjunto adecuado de números contables para los conjuntos subcontables puede no ser recursivo. En una teoría de conjunto, las teorías de las matemáticas se modelan. Por ejemplo, en la teoría de conjuntos, "el" conjunto de números reales se identifica como un conjunto que cumple algunos axiomas de números reales. Se han estudiado varios modelos, como los reales de Dedekind o los reales de Cauchy. Los axiomas Weaker significan menos restricciones y así permiten una clase más rica de modelos. En consecuencia, en un contexto de otra manera constructivo (la ley de centro excluido no tomada como axioma), es consistente en adoptar axiomas no clásicos que contradicen las consecuencias de la ley de medio excluido. Por ejemplo, el espacio incontable de funciones ${displaystyle {Mathbb {N}to {0,1}$ puede afirmarse que es subcontable, noción de tamaño ortogonal a la declaración ${fnMicrosoft Sans Serif} {fnh}\fnh}to\\top,1}\\\\\\\\\\\fnMicrosoft}$ . En tal contexto, es posible la subcontratabilidad de todos los conjuntos, o las inyecciones de los incontables ${displaystyle {Mathbb {N}. {N}$ en ${displaystyle {Mathbb {N}}$ .

Preguntas abiertas

Motivado por la idea de que el conjunto de números reales es "más grande" que el conjunto de los números naturales, uno se pregunta si hay un conjunto cuya cardinalidad es "entre" la de los enteros y la de los reales. Esta pregunta lleva a la famosa hipótesis del continuo. De manera similar, la pregunta de si existe un conjunto cuya cardinalidad está entre |S| y |P(S)| para algún S infinito conduce a la hipótesis del continuo generalizado.

Diagonalización en un contexto más amplio

La paradoja de Russell ha demostrado que la teoría de conjuntos ingenua, basada en un esquema de comprensión sin restricciones, es contradictoria. Tenga en cuenta que existe una similitud entre la construcción de T y el conjunto en la paradoja de Russell. Por lo tanto, dependiendo de cómo modifiquemos el esquema del axioma de comprensión para evitar la paradoja de Russell, argumentos como la inexistencia de un conjunto de todos los conjuntos pueden o no seguir siendo válidos.

Los análogos del argumento diagonal se usan ampliamente en matemáticas para probar la existencia o inexistencia de ciertos objetos. Por ejemplo, la prueba convencional de la imposibilidad de resolver el problema de la detención es esencialmente un argumento diagonal. Además, la diagonalización se usó originalmente para mostrar la existencia de clases de complejidad arbitrariamente duras y desempeñó un papel clave en los primeros intentos de demostrar que P no es igual a NP.

Versión para las Nuevas Fundaciones de Quine

La prueba anterior falla para la obra "New Foundations" de W. V. Quine. teoría de conjuntos (NF). En NF, el esquema del axioma ingenuo de comprensión se modifica para evitar las paradojas mediante la introducción de una especie de "local" teoría de tipos. En este esquema de axiomas,

{} s ▪ S: s ∉ f()s)

es no un conjunto, es decir, no satisface el esquema del axioma. Por otro lado, podríamos intentar crear un argumento diagonal modificado al notar que

{} s ▪ S: s ∉ f({s}

es un conjunto en NF. En cuyo caso, si P₁(S) es el conjunto de subconjuntos de un elemento de S y f es una biyección propuesta de P₁(S) a P(S), uno puede usar prueba por contradicción para probar que |P₁(S)| < |P(S)|.

La prueba sigue por el hecho de que si f fuera de hecho un mapa sobre P( S), entonces podríamos encontrar r en S, tal que f({r}) coincide con el conjunto diagonal modificado, arriba. Concluiríamos que si r no está en f({r}), entonces r está en f({r}) y viceversa.

No es posible poner P₁(S) en una relación de uno a uno con S, ya que los dos tienen diferentes tipos, por lo que cualquier función así definida violaría las reglas de escritura para el esquema de comprensión.