Ventaja mecanica
Ventaja mecánica es una medida de la amplificación de fuerza lograda mediante el uso de una herramienta, dispositivo mecánico o sistema de máquina. El dispositivo compensa las fuerzas de entrada contra el movimiento para obtener una amplificación deseada en la fuerza de salida. El modelo para esto es la ley de la palanca. Los componentes de la máquina diseñados para gestionar las fuerzas y el movimiento de esta manera se denominan mecanismos. Un mecanismo ideal transmite potencia sin sumar ni restar. Esto significa que la máquina ideal no incluye una fuente de energía, no tiene fricción y está construida con cuerpos rígidos que no se desvían ni se desgastan. El rendimiento de un sistema real en relación con este ideal se expresa en términos de factores de eficiencia que tienen en cuenta las desviaciones del ideal.
Palanca
La palanca es una barra móvil que pivota sobre un punto de apoyo unido o colocado sobre un punto fijo. La palanca funciona aplicando fuerzas a diferentes distancias del punto de apoyo o pivote. La ubicación del fulcro determina la clase de una palanca. Cuando una palanca gira continuamente, funciona como una palanca giratoria de segunda clase. El movimiento del punto final de la palanca describe una órbita fija, donde se puede intercambiar energía mecánica. (ver una manivela como ejemplo).
En los tiempos modernos, este tipo de apalancamiento giratorio se usa mucho; ver una palanca (giratoria) de segunda clase; ver engranajes, poleas o accionamiento por fricción, utilizados en un esquema de transmisión de potencia mecánica. Es común que la ventaja mecánica sea manipulada en un 'colapsado' forma, a través del uso de más de un engranaje (un juego de engranajes). En tal conjunto de engranajes, se utilizan engranajes que tienen radios más pequeños y menos ventajas mecánicas inherentes. Para hacer uso de la ventaja mecánica no colapsada, es necesario usar una 'longitud verdadera' palanca giratoria Ver, también, la incorporación de ventajas mecánicas en el diseño de ciertos tipos de motores eléctricos; un diseño es un 'outrunner'.
A medida que la palanca pivota sobre el punto de apoyo, los puntos más alejados de este pivote se mueven más rápido que los puntos más cercanos al pivote. La potencia que entra y sale de la palanca es la misma, por lo que debe salir igual cuando se realizan los cálculos. La potencia es el producto de la fuerza y la velocidad, por lo que las fuerzas aplicadas a puntos más alejados del pivote deben ser menores que cuando se aplican a puntos más cercanos.
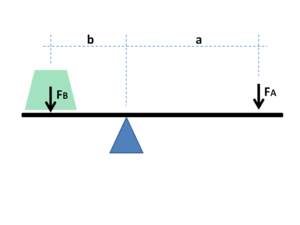
Si a y b son distancias desde el punto de apoyo a los puntos A y B y si la fuerza FA aplicada a A es la fuerza de entrada y FB ejercida en B es la salida, la relación de las velocidades de los puntos A y B viene dada por a/b por lo que la relación entre la fuerza de salida y la fuerza de entrada, o la ventaja mecánica, está dada por
- MA=FbFa=ab.{displaystyle {Mathit {MA}={frac} {fnK} {f}} {fnMicroc}}} {fnMicroc} {f}}} {f} {f}}}}} {f}}}}}}} {fnMicroc} {a}{b}.}
Esta es la ley de la palanca, que fue demostrada por Arquímedes mediante razonamiento geométrico. Muestra que si la distancia a desde el fulcro hasta donde se aplica la fuerza de entrada (punto A) es mayor que la distancia b desde el fulcro donde se aplica la fuerza de salida (punto B), entonces la palanca amplifica la fuerza de entrada. Si la distancia desde el fulcro a la fuerza de entrada es menor que la distancia desde el fulcro a la fuerza de salida, entonces la palanca reduce la fuerza de entrada. Reconociendo las profundas implicaciones y los aspectos prácticos de la ley de la palanca, a Arquímedes se le ha atribuido la famosa cita "Dame un lugar para pararme y con una palanca moveré el mundo entero".
El uso de la velocidad en el análisis estático de una palanca es una aplicación del principio del trabajo virtual.
Relación de velocidad
El requisito de entrada de energía a un mecanismo ideal para igualar la salida de energía proporciona una forma sencilla de calcular la ventaja mecánica a partir de la relación de velocidad de entrada-salida del sistema.
La potencia de entrada a un tren de engranajes con un par TA aplicado a la polea de transmisión que gira a una velocidad angular de ωA es P=TAωA.
Debido a que el flujo de potencia es constante, el par TB y la velocidad angular ωB de la salida el engranaje debe satisfacer la relación
- P=TA⋅ ⋅ A=TB⋅ ⋅ B,{displaystyle P=T_{A}omega ##{A}=T_{B}omega ¡No!
que produce
- MA=TBTA=⋅ ⋅ A⋅ ⋅ B.{displaystyle {Mathit {MA}={frac} {fnK} {fnMicroc}} {fnMicroc}} {fnK}} {fnK}}}} {fnK}}} {fnK}}} {fnK} {fnK}}}}} {fnK}}}}}} {fnKf}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}} {f} {f} {f} {f} {f} {f}f}f}f}f}f}f}f}}}f}f}fnf}fnf}f}fnf}fnfnfnf}}fnfnfnfnfnf}}fnKf}fnf}}}}fnK {omega ###{A}{omega - Sí.
Esto muestra que para un mecanismo ideal, la relación de velocidad de entrada-salida es igual a la ventaja mecánica del sistema. Esto se aplica a todos los sistemas mecánicos, desde robots hasta conexiones.
Trenes de engranajes
Los dientes de los engranajes están diseñados para que el número de dientes de un engranaje sea proporcional al radio de su círculo primitivo y para que los círculos primitivos de los engranajes engranados rueden entre sí sin deslizarse. La relación de velocidad para un par de engranajes engranados se puede calcular a partir de la relación de los radios de los círculos primitivos y la relación del número de dientes en cada engranaje, su relación de transmisión.
La velocidad v del punto de contacto en los círculos de paso es la misma en ambos engranajes y viene dada por
- v=rA⋅ ⋅ A=rB⋅ ⋅ B,{displaystyle v=r_{A}omega ## {A}=r_{B}omega ¡No!
donde el engranaje de entrada A tiene un radio rA y engrana con el engranaje de salida B de radio rB, por lo tanto,
- ⋅ ⋅ A⋅ ⋅ B=rBrA=NBNA.{displaystyle {frac {omega ###{A}{omega ¿Qué? {fnK} {f}} {fnMicroc}}} {fnMicroc}} {N_{B} {N_{A}}}}
donde NA es el número de dientes en el engranaje de entrada y NB es el número de dientes en el engranaje de salida.
La ventaja mecánica de un par de engranajes engranados en los que el engranaje de entrada tiene NA dientes y el engranaje de salida tiene NB dientes viene dado por
- MA=rBrA=NBNA.{displaystyle {Mathit {MA}={frac} {fnK} {f}} {fnMicroc}}} {fnMicroc}} {N_{B} {N_{A}}}}
Esto muestra que si el engranaje de salida GB tiene más dientes que el engranaje de entrada GA, entonces el tren de engranajes amplifica el par de entrada. Y, si el engranaje de salida tiene menos dientes que el engranaje de entrada, entonces el tren de engranajes reduce el par de entrada.
Si el engranaje de salida de un tren de engranajes gira más lentamente que el engranaje de entrada, entonces el tren de engranajes se denomina reductor de velocidad (multiplicador de fuerza). En este caso, debido a que el engranaje de salida debe tener más dientes que el engranaje de entrada, el reductor de velocidad amplificará el par de entrada.
Accionamientos por cadena y correa
Los mecanismos que consisten en dos ruedas dentadas conectadas por una cadena o dos poleas conectadas por una correa están diseñados para proporcionar una ventaja mecánica específica en los sistemas de transmisión de potencia.
La velocidad v de la cadena o correa es la misma cuando está en contacto con los dos piñones o poleas:
- v=rA⋅ ⋅ A=rB⋅ ⋅ B,{displaystyle v=r_{A}omega ## {A}=r_{B}omega ¡No!
donde la rueda dentada o polea de entrada A engrana con la cadena o correa a lo largo del radio de paso rA y la rueda dentada o polea de salida B engrana con esta cadena o correa a lo largo del radio de paso rB,
por lo tanto
- ⋅ ⋅ A⋅ ⋅ B=rBrA=NBNA.{displaystyle {frac {omega ###{A}{omega ¿Qué? {fnK} {f}} {fnMicroc}}} {fnMicroc}} {N_{B} {N_{A}}}}
donde NA es el número de dientes en la rueda dentada de entrada y NB es el número de dientes en la rueda dentada de salida. Para una transmisión por correa dentada, se puede utilizar el número de dientes de la rueda dentada. Para transmisiones por correa de fricción, se debe utilizar el radio de paso de las poleas de entrada y salida.
La ventaja mecánica de un par de transmisión por cadena o transmisión por correa dentada con una rueda dentada de entrada con dientes NA y la rueda dentada de salida tiene NB vienen dados por
- MA=TBTA=NBNA.{displaystyle {Mathit {MA}={frac} {fnK} {fnMicroc}} {fnMicroc}} {fnK}} {fnK}}}} {fnK}}} {fnK}}} {fnK} {fnK}}}}} {fnK}}}}}} {fnKf}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}} {f} {f} {f} {f} {f} {f}f}f}f}f}f}f}f}}}f}f}fnf}fnf}f}fnf}fnfnfnf}}fnfnfnfnfnf}}fnKf}fnf}}}}fnK {N_{B} {N_{A}}}}
La ventaja mecánica de las transmisiones por correa de fricción viene dada por
- MA=TBTA=rBrA.{displaystyle {Mathit {MA}={frac} {fnK} {fnMicroc}} {fnMicroc}} {fnK}} {fnK}}}} {fnK}}} {fnK}}} {fnK} {fnK}}}}} {fnK}}}}}} {fnKf}} {f}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}} {f} {f} {f} {f} {f} {f}f}f}f}f}f}f}f}}}f}f}fnf}fnf}f}fnf}fnfnfnf}}fnfnfnfnfnf}}fnKf}fnf}}}}fnK {fnMicrosoft Sans Serif}
Las cadenas y las correas disipan la potencia a través de la fricción, el estiramiento y el desgaste, lo que significa que la potencia de salida es menor que la potencia de entrada, lo que significa que la ventaja mecánica del sistema real será menor que la calculada para un mecanismo ideal. Una transmisión por cadena o correa puede perder hasta un 5 % de la potencia a través del sistema debido al calor por fricción, la deformación y el desgaste, en cuyo caso la eficiencia de la transmisión es del 95 %.
Ejemplo: transmisión por cadena de bicicleta

Considere la bicicleta de 18 velocidades con bielas de 7 pulgadas (radio) y ruedas de 26 pulgadas (diámetro). Si las ruedas dentadas en el cigüeñal y en la rueda motriz trasera son del mismo tamaño, entonces la relación entre la fuerza de salida sobre la llanta y la fuerza de entrada sobre el pedal se puede calcular a partir de la ley de la palanca para ser
- MA=FBFA=713=0,54.{displaystyle {Mathit {MA}={frac} {fnK} {f} {fnK}} {fnMicroc}} {f}}} {f} {f}}} {f}}} {f}}}}} {fnMicroc}} {f}}} {f}} {f}}}}} {f}}}}}} {f}f}f}f}f}f}f}}}f}f}f}f}f}}f}f} {7}=0.54}
Ahora, suponga que las ruedas dentadas delanteras tienen una opción de 28 y 52 dientes, y que las ruedas dentadas traseras tienen una opción de 16 y 32 dientes. Usando diferentes combinaciones, podemos calcular las siguientes relaciones de velocidad entre las ruedas dentadas delanteras y traseras
| entrada (pequeña) | entrada (grande) | producción (pequeña) | producción (grande) | ratio de velocidad | ratio crank-wheel | total de MA | |
|---|---|---|---|---|---|---|---|
| baja velocidad | 28 | - | - | 32 | 1.14 | 0,544 | 0,622 |
| mitad | - | 52 | - | 32 | 0,622 | 0,544 | 0.33 |
| mitad | 28 | - | 16 | - | 0,57 | 0,544 | 0.31 |
| alta velocidad | - | 52 | 16 | - | 0.30 | 0,544 | 0.16 |
La relación entre la fuerza que impulsa la bicicleta y la fuerza sobre el pedal, que es la ventaja mecánica total de la bicicleta, es el producto de la relación de velocidad (o relación de dientes del piñón de salida/piñón de entrada) y el cigüeñal. relación de palanca de rueda.
Observe que, en todos los casos, la fuerza sobre los pedales es mayor que la fuerza que impulsa la bicicleta hacia adelante (en la ilustración de arriba, se indica la correspondiente fuerza de reacción dirigida hacia atrás sobre el suelo).
Bloqueo y placaje
Un polipasto es un conjunto de cuerda y poleas que se utiliza para levantar cargas. Se ensamblan varias poleas para formar los bloques, uno fijo y otro que se mueve con la carga. La cuerda se enhebra a través de las poleas para proporcionar una ventaja mecánica que amplifique esa fuerza aplicada a la cuerda.
Para determinar la ventaja mecánica de un sistema de bloqueo y aparejo, considere el caso simple de un aparejo de pistola, que tiene una sola polea montada o fija y una sola polea móvil. La cuerda se enrosca alrededor del bloque fijo y cae al bloque móvil donde se enhebra alrededor de la polea y se vuelve a subir para anudarla al bloque fijo.
Sea S la distancia desde el eje del bloque fijo hasta el extremo de la cuerda, que es A donde se aplica la fuerza de entrada. Sea R la distancia desde el eje del bloque fijo al eje del bloque móvil, que es B donde se aplica la carga.
La longitud total de la cuerda L se puede escribir como
- L=2R+S+K,{displaystyle L=2R+S+K,!}
donde K es la longitud constante de la cuerda que pasa sobre las poleas y no cambia a medida que se mueve el polipasto.
Las velocidades VA y VB de los puntos A y B están relacionados por la longitud constante de la cuerda, es decir
- LÍ Í =2RÍ Í +SÍ Í =0,{displaystyle { dot}=2{dot {R}+{dot {S}=0,}
o
- SÍ Í =− − 2RÍ Í .{displaystyle { dot}=-2{dot {R}}
El signo negativo muestra que la velocidad de la carga es opuesta a la velocidad de la fuerza aplicada, lo que significa que cuando tiramos de la cuerda hacia abajo, la carga se mueve hacia arriba.
Sea VA positivo hacia abajo y VB positivo hacia arriba, entonces esta relación se puede escribir como la relación de velocidad
- VAVB=SÍ Í − − RÍ Í =2,{fnMicroc {fnh} {fnh}} {fnMicroc {fnh} {fnh} {f} {fn}} {fnMicroc}} {fnh} {fn} {fnh} {f}}} {fnhfnf}} {f}}}}}} {f}}}} {f}}}}}}}}f}}}}}}}} {f}}}}}}}}}} {f} {f} {f}}}}}f}f}}}}}f}f}}f}} {fnh}}}}}}}}}} {cf}}}}f}f}f}f} {f}f}fn}fnh}f}}fnf}}f}fnh}}}}}} {R}}=2,}
donde 2 es el número de secciones de cuerda que soportan el bloque en movimiento.
Sea FA la fuerza de entrada aplicada en A el extremo de la cuerda, y sea F B sea la fuerza en B sobre el bloque en movimiento. Al igual que las velocidades FA se dirige hacia abajo y FB se dirige hacia arriba.
Para un sistema ideal de poleas y aparejos, no hay fricción en las poleas ni desviación ni desgaste en la cuerda, lo que significa que la entrada de potencia por la fuerza aplicada FA</sub VA debe ser igual a la potencia que actúa sobre la carga FBV B, eso es
- FAVA=FBVB.{displaystyle F_{A}V_{B}
La relación entre la fuerza de salida y la fuerza de entrada es la ventaja mecánica de un sistema ideal de aparejos de armas,
- MA=FBFA=VAVB=2.{displaystyle {Mathit {MA}={frac} {fnK} {f} {fnK}} {fnMicroc}} {f}}} {f} {f}}} {f}}} {f}}}}} {fnMicroc}} {f}}} {f}} {f}}}}} {f}}}}}} {f}f}f}f}f}f}f}}}f}f}f}f}f}}f}f} [V_{A} {V_{B}=2.]
Este análisis se generaliza a un bloqueo y aparejo ideal con un bloque en movimiento sostenido por n secciones de cuerda,
- MA=FBFA=VAVB=n.{displaystyle {Mathit {MA}={frac} {fnK} {f} {fnK}} {fnMicroc}}} {f}} {f}} {f}}}}} {f}}} {f}}} {fnMicroc} {f}}}} {f}} {f}}}} {f}}}}}}}}}}} {f} {f}f}f}f} {f}f}f} ¡No!
Esto muestra que la fuerza ejercida por un bloque y un aparejo ideales es n veces la fuerza de entrada, donde n es el número de secciones de cuerda que soportan el bloque en movimiento.
Eficiencia
La ventaja mecánica que se calcula suponiendo que no se pierde potencia por la desviación, la fricción y el desgaste de una máquina es el rendimiento máximo que se puede lograr. Por esta razón, a menudo se denomina ventaja mecánica ideal (IMA). En funcionamiento, la desviación, la fricción y el desgaste reducirán la ventaja mecánica. La cantidad de esta reducción de la ventaja mecánica ideal a la real (AMA) está definida por un factor llamado eficiencia, una cantidad que se determina mediante experimentación.
Como ejemplo, usar un bloque y aparejo con seis secciones de cuerda y una carga de 600 lb, el operador de un sistema ideal tendría que tirar de la cuerda seis pies y ejercer 100 lbF de fuerza para levantar la carga un pie. Ambas relaciones Fout / Fin y Vin / Vout muestran que el IMA es seis. Para la primera proporción, 100 lbF de entrada forzada da como resultado 600 lb F de salida forzada. En un sistema real, la fuerza de salida sería de menos de 600 libras debido a la fricción en las poleas. La segunda relación también arroja una MA de 6 en el caso ideal pero un valor menor en el escenario práctico; no tiene en cuenta adecuadamente las pérdidas de energía, como el estiramiento de la cuerda. Restar esas pérdidas de la IMA o usar la primera proporción produce la AMA.
Ventaja mecánica ideal
La ventaja mecánica ideal (IMA), o ventaja mecánica teórica, es la ventaja mecánica de un dispositivo con el supuesto de que sus componentes no se flexionan, no hay fricción, y no hay desgaste. Se calcula utilizando las dimensiones físicas del dispositivo y define el rendimiento máximo que puede alcanzar el dispositivo.
Los supuestos de una máquina ideal son equivalentes al requisito de que la máquina no almacene ni disipe energía; la potencia que entra en la máquina es igual a la potencia que sale. Por lo tanto, la potencia P es constante a través de la máquina y la fuerza por la velocidad que entra en la máquina es igual a la fuerza por la velocidad que sale, es decir,
- P=Fdentrovdentro=FFuera.vFuera..{displaystyle P=F_{text{in}v_{in}=F_{text{out}v_{text{out}}}
La ventaja mecánica ideal es la relación entre la fuerza que sale de la máquina (carga) y la fuerza que entra en la máquina (esfuerzo), o
- IMA=FFuera.Fdentro.{displaystyle {Mathit {IMA}={frac} {F_{text{out}} {F_{in}}}} {f} {f}}} {f}} {f}} {f}}}}}} {f}}} {f}}}}}} {f}}}} {f}}} {f}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}} {f} {f}}}}}} {f}}}}}}}}}} {f}}}}}}}}}}}}}}}}}} {f}} {f}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {
La aplicación de la relación de potencia constante produce una fórmula para esta ventaja mecánica ideal en términos de relación de velocidad:
- IMA=FFuera.Fdentro=vdentrovFuera..{displaystyle {Mathit {IMA}={frac} {fnK} {f} {fnK}}}={f}} {f}} {f}}} {f}}}} {fn}}}}} {f}} {fn}}}}}} {f}}} {f} {f}}}} {f}}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}} {f}}} {f}}}}}}} {f}}}}} {f}} {f}}}}}} {f}}}}}}}}} {f}}}}} {f} {f} {f}}}}}}}}}}}}}} {f} {f}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {V_{text{in}} {v_{text{out}}}} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft Sans Serif} {fnK}}}}}} {fnK}} {f}}} {f}}}}}}} {f}}}}}}}}}}}}} {f}}}}} {f}}}}} {f}}}}}}}}}}} {f}} {f}}}}}} {f}}}}}}}} {f}}}}}}}}}} {f}}}}} {f} {f}}}} {f}}}}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
La relación de velocidad de una máquina se puede calcular a partir de sus dimensiones físicas. La suposición de potencia constante permite utilizar la relación de velocidad para determinar el valor máximo de la ventaja mecánica.
Ventaja mecánica real
La ventaja mecánica real (AMA) es la ventaja mecánica determinada por la medición física de las fuerzas de entrada y salida. La ventaja mecánica real tiene en cuenta la pérdida de energía debido a la desviación, la fricción y el desgaste.
La AMA de una máquina se calcula como la relación entre la salida de fuerza medida y la entrada de fuerza medida,
- AMA=FFuera.Fdentro,{displaystyle {Mathit {AMA}={frac} {F_{text{out}} {F_{in}}} {f}} {f}}} {f}} {f}} {f}}}}} {f}}} {f}}}}}}} {f}}}} {f}}} {f}}}} {f}}}}} {f}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
donde las fuerzas de entrada y salida se determinan experimentalmente.
La relación entre la ventaja mecánica determinada experimentalmente y la ventaja mecánica ideal es la eficiencia mecánica η de la máquina,
- .. =AMAIMA.{displaystyle eta ={frac {matit {AMA}{mathit {IMA}}}}}
Contenido relacionado
Pascal (unidad)
Trabajo (física)
Número de Prandtl