Tridecágono

En geometría, un tridecágono o triskaidecágono o 13 gónos es un polígono de trece lados.

Tridecágono regular

Un tridecágono regular está representado por el símbolo de Schläfli {13}.

La medida de cada ángulo interno de un tridecágono regular es aproximadamente 152,308 grados, y el área con longitud de lado a está dada por

${displaystyle A={13} {4}a}c}cccH0}fnK} } {13}simeq 13.1858,a^{2}$

Construcción

Como 13 es un primo de Pierpont pero no un primo de Fermat, el tridecágono regular no se puede construir usando un compás y una regla. Sin embargo, se puede construir utilizando neusis o un trisector de ángulo.

Lo siguiente es una animación de una construcción de neusis de un tridecagon regular con radio de circuncircle ${displaystyle {overline {}=12,}$ según Andrew M. Gleason, basado en la trisección de ángulo por medio del Tomahawk (azul claro).

Aquí se muestra una construcción aproximada de un tridecágono regular usando regla y compás.

Otra posible animación de una construcción aproximada, también posible con el uso de regla y compás.

Basado en el círculo unitario r = 1 [unidad de longitud]

• Longitud lateral construida en GeoGebra ${displaystyle a=0.478631328575115;[{text{unit of length}}}}$
• Longitud lateral del tridecagon ${displaystyle a_{text{target}=rcdot 2cdot sin left({frac {180^{circ }}{13}}}right)=0.478631328575115ldots ;[{text{unit of length}}}}}}}}}}}}}}$
• Error absoluto de la longitud lateral construida:

Hasta la máxima precisión de 15 lugares decimales, el error absoluto es ${displaystyle F_{a}=a-a_{text{target}=0.0;[{text{unit of length}}}$

• Ángulo central construido del tridecagón en GeoGebra (display significant 13 decimal places, rounded) ${displaystyle mu =27.6923076923077^{circ }$
• Ángulo central de tridecagon ${displaystyle mu _{text{target}=left({frac {360^{circ {}{13}right)=27.{overline {692307}{circ }}$
• Error angular absoluto del ángulo central construido:

Hasta 13 lugares decimales, el error absoluto es ${displaystyle F_{mu }=mu -mu _{text{target}=0.0^{circ }$

Ejemplo para ilustrar el error

En un círculo circunscrito de radio r = mil millones de kilómetros (una distancia que la luz tardaría aproximadamente 55 minutos en recorrer), el error absoluto en la longitud del lado construido sería menor que 1 mm.

Simetría

El tridecágono regular tiene simetría Dih13, orden 26. Como 13 es un número primo, hay un subgrupo con simetría diédrica: Dih₁, y 2 simetrías de grupo cíclico: Z₁₃ y Z₁.

Estas 4 simetrías se pueden ver en 4 simetrías distintas en el tridecágono. John Conway los etiqueta mediante letras y orden de grupo. La simetría completa de la forma regular es r26 y ninguna simetría está etiquetada como a1. Las simetrías diédricas se dividen dependiendo de si pasan por vértices (d para diagonal) o aristas (p para perpendiculares), y i cuando la reflexión trayectoria de líneas a través de aristas y vértices. Las simetrías cíclicas en la columna del medio están etiquetadas como g por sus órdenes de giro central.

Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Sólo el subgrupo g13 no tiene grados de libertad pero puede verse como aristas dirigidas.

Uso numismático

El tridecágono regular se utiliza como forma de la moneda de 20 coronas checas.

Polígonos relacionados

Un tridecagrama es un polígono estrella de 13 lados. Hay cinco formas regulares dadas por los símbolos de Schläfli: {13/2}, {13/3}, {13/4}, {13/5} y {13/6}. Como 13 es primo, ninguno de los tridecagramos son figuras compuestas.

Tridecagramas
Imagen	{13/2}	{13/3}	{13/4}	{13/5}	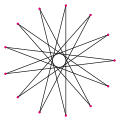{13/6}
Ángulo interno	Entendido124.615°	♥96.9231°	/64/69.2308°	■41.5385°	■13.8462°

Polígonos de Petrie

El tridecágono regular es el polígono de Petrie 12-simplex:

A12
12-simplex