Trapezoedro

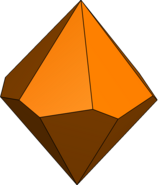
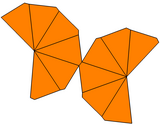
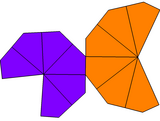
En geometría, una n-gonal trapezoedro, n-trapezoedro, n-antidipiramid, n-antibipiramid, o n-deltoedro es el dual poliedro de un antiprisma n-gonal. Las 2n caras de un n-trapezohedron son congruentes y están escalonados simétricamente; se les llama cometas retorcidas. De mayor simetría, sus caras 2n son cometas (también llamadas deltoides).

El "n-gonal" parte del nombre aquí no se refiere a caras, sino a dos disposiciones de cada n vértices alrededor de un eje de n-fold simetría. El antiprisma dual n-gonal tiene dos n-gon caras.

Un trapezoedro n-gonal se puede diseccionar en dos < span class="nowrap">n-gonal pirámides y una n-gonal antiprisma.

Terminología

Estas figuras, a veces llamadas deltoedro, no deben confundirse con los deltaedros, cuyas caras son triángulos equiláteros.

Trapezoedros trigonal, tetragonal y hexagonal retorcidos (con seis, ocho y doce cometas congruentes retorcidas) caras) existen como cristales; en cristalografía (que describe los hábitos cristalinos de los minerales), se les llama simplemente trigonal, tetragonal y trapezoedros hexagonales. No tienen plano de simetría ni centro de simetría de inversión;^, pero tienen un centro de simetría: el punto de intersección de sus ejes de simetría. El trapezoedro trigonal tiene un eje de simetría triple, perpendicular a tres ejes de simetría doble. El trapezoedro tetragonal tiene un eje de simetría cuádruple, perpendicular a cuatro ejes de simetría doble de dos tipos. El trapezoedro hexagonal tiene un eje de simetría de 6 veces, perpendicular a seis ejes de simetría de 2 veces de dos tipos.

Las disposiciones cristalinas de átomos pueden repetirse en el espacio con células de trapezoedro trigonales y hexagonales.

También en cristalografía, la palabra trapezoedro se usa a menudo para el poliedro con 24 caras de cometa congruentes no retorcidas, conocido propiamente como icositetraedro deltoidal, que tiene dieciocho ordenes. 4 vértices y ocho vértices de orden 3. Esto no debe confundirse con el trapezoedro dodecagonal, que también tiene 24 caras de cometa congruentes, pero dos ápices de orden 12 (es decir, polos) y dos anillos de doce vértices de orden 3 cada uno.

Aún en cristalografía, el dodecaedro deltoide tiene 12 caras de cometa no torcidas congruentes, seis vértices de orden 4 y ocho vértices de orden 3 (el dodecaedro rómbico es un caso especial). Esto no debe confundirse con el trapezoedro hexagonal, que también tiene 12 caras de cometa congruentes, pero dos ápices de orden 6 (es decir, polos) y dos anillos de seis vértices de orden 3 cada uno.

Formularios

Un n-trapezoedro se define mediante una inclinación regular en zig-zag Base de 2n-gón, dos ápices simétricos sin grado de libertad justo encima y justo debajo de la base, y caras cuadriláteras que conectan cada par de los bordes basales adyacentes a un ápice.

Un n-trapezoedro tiene dos vértices apicales en su eje polar, y 2< i>n vértices basales en dos anillos regulares n-gonales. Tiene 2n caras de cometa congruentes y es isoédrico.

Familia de n- trampa mortal

Nombre de Trapezohedron	Digonal trapezohedron (Tetraedro)	Trigonal trapezohedron	Tetragonal trapezohedron	Pentagonal trapezohedron	Hexagonal trapezohedron	Heptagonal trapezohedron	trapezohedro Octagonal	Decagonal trapezohedron	Dodecagonal trapezohedron	...	Apeirogonal trapezohedron
Imagen de poliedro										...
Imagen de revestimiento esférico										Imagen de azulado plano
Configuración facial	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V dieta.3.3.3

Casos especiales:

• n = 2. Una forma degenerada de trapezohedro: un tetraedro geométrico con 6 vértices, 8 bordes y 4 caras degeneradas que se degeneran en triángulos. Su doble es una forma degenerada de antiprisma: también un tetraedro.

• n = 3. El doble de un antiprisma triangular: los kites son rhombi (o cuadrados); por lo tanto estos trapezohedra son también zonohedra. Se llaman rhombohedra. Son cubos escalados en la dirección de un cuerpo diagonal. También son los paralelos con rostros rhombic congruentes.

  

  • Un caso especial de un rhombohedron es uno en el que los rhombi formando los rostros tienen ángulos de 60° y 120°. Se puede descomponer en dos iguales tetrahedra regular y un octaedro regular. Puesto que los paralelos pueden llenar el espacio, por lo que puede una combinación de tetrahedra regular y octahedra regular.

• n = 5. El trapezohedro pentagonal es el único poliedro aparte de los sólidos platónicos usados comúnmente como una muerte en juegos de rol como Dungeons " Dragons. Siendo convexa y transitiva facial, hace dados justos. Tener 10 lados, se puede utilizar en la repetición para generar cualquier probabilidad uniforme decimal deseada. Típicamente, dos dados de diferentes colores se utilizan para los dos dígitos para representar números de 00 a 99.

Simetría

El grupo de simetría de un trapezoedro n-gonal es D_nd = D_nv, de orden 4n, excepto en el caso de n = 3: un cubo tiene el grupo de simetría más grande O_d de orden 48 = 4×(4×3), que tiene cuatro versiones de D_3d como subgrupos.

El grupo de rotación de un trapezoedro n es D _n, de orden 2n, excepto en el caso de n = 3: un cubo tiene el grupo de rotación más grande O de orden 24 = 4× (2×3), que tiene cuatro versiones de D₃ como subgrupos.

Nota: Cada n-trapezoedro con una inclinación regular en zig-zag Base de 2n-gon y 2n caras de cometa no torcidas congruentes tiene la mismo grupo de simetría (diédrico) que el n-trapezoedro de uniforme dual, para n ≥ 4.

Un grado de libertad dentro de la simetría desde D_nd (orden 4n) hasta D_n (orden 2n) cambia las cometas congruentes en cuadriláteros congruentes con tres longitudes de aristas, llamados cometas retorcidas, y el n-trapezoedro se llama trapezoedro retorcido. (En el límite, un borde de cada cuadrilátero tiene una longitud cero y el trapezoedro n se convierte en una bipirámide n).

Si las cometas que rodean los dos picos no están torcidas sino que tienen dos formas diferentes, el trapezoedro n sólo puede tener C_nv simetría (cíclica con espejos verticales), orden 2n, y se llama trapezoedro desigual o asimétrico. Su dual es un n-antiprisma desigual, con los n-gonos superior e inferior de diferentes radios.

Si las cometas están torcidas y tienen dos formas diferentes, el trapezoedro n sólo puede tener simetría C_n (cíclica), orden n, y se llama trapezoedro torcido desigual.

Ejemplo: variaciones con trapezohedra hexagonal ()n = 6)

Trapezohedron tipo	Twisted trapezohedron		Unequal trapezohedron	Unequal twisted trapezohedron
Grupo de simetría	D6, (662), [6,2]+		C6v, (*66), [6]	C6, (66), [6]+
Imagen de poliedro
Net

Star trapezohedron

A estrella p/q- Trapezohedron (donde) 2 ≤ q c) 1p) se define por una estrella de zig-zag regular 2p/q-gon base, dos apices simétricos sin grado de libertad justo arriba y justo debajo de la base, y caras cuadrilaterales que conectan cada par de bordes basales adyacentes a un ápice.

Una estrella p/q-trapezohedron tiene dos vértices apicales en su eje polar, y 2p vértices basales en dos vertices regulares p- anillos pasados. Tiene 2p caras de cometa congruentes, y es isohedral.

Tal estrella p/q-trapezoedro es un autointersectante, Forma cruzada o no convexa. Existe para cualquier estrella sesgada en zig-zag regular 2p/q-base de gón (donde 2 ≤ q < 1p).

Pero si p/q < 3/ 2, luego (p − q)360°/p < q/< span class="den">2360°/p, por lo que el antiprisma de estrella dual (del trapezoedro de estrella) no puede ser uniforme (es decir, no puede tener bordes de longitudes iguales); y si p/q = 3/2, luego < span class="texhtml">(p − q)360° /p = q/2360°/< /span>p, por lo que el antiprisma de estrella dual debe ser plano, por lo tanto degenerado, para ser uniforme.

Una estrella dual-uniforme p/q- Trapezohedron tiene el diagrama Coxeter-Dynkin .

Estrella dual-uniform p/q- Trapezohedra hasta p= 12

5/2	5/3	7/2	7/3	7/4	8/3	8/5	9/2	9/4	9/5

10/3	11/2	11/3	11/4	11/5	11/6	11/7	12/5	12/7