Tetraedro

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Poliedro con 4 caras

Tetraedro regular
(Haga clic aquí para el modelo giratorio)
Tipo	sólido platónico
Elementos	F = 4, E = 6 V = 4 (χ = 2)
Caras por lados	4{3}
Notación de Conway	T
Símbolos de Schläfli	{3,3}
Símbolos de Schläfli	h{4,3}, s{2,4}, sr{2,2}
Configuración facial	V3.3.3
Signatura Wythoff	3 Silencio 2 3 TENIDA 2 2 2
Coxeter diagrama	=
Simmetría	Td, A₃, [3,3], (*332)
Grupo de rotación	T, [3,3]⁺, (332)
Referencias	U₀₁, C₁₅, W₁
Propiedades	regular, convexdeltahedron
Ángulo Dihedral	70.528779° = arcos1.3)
3.3.3 (Vertex figure)	Auto-dual (poliedro dual)
Cifras netas

Tetraedro (Matemateca IME-USP)

Modelo 3D de tetraedro regular.

En geometría, un tetraedro (plural: tetraedros o tetraedros), también conocido como pirámide triangular, es un poliedro compuesto por cuatro caras triangulares, seis aristas rectas y cuatro vértices. El tetraedro es el más simple de todos los poliedros convexos ordinarios.

El tetraedro es el caso tridimensional del concepto más general de simplex euclidiano y, por lo tanto, también puede denominarse 3-simplex.

El tetraedro es un tipo de pirámide, que es un poliedro con una base poligonal plana y caras triangulares que conectan la base con un punto común. En el caso de un tetraedro la base es un triángulo (cualquiera de las cuatro caras puede considerarse la base), por lo que un tetraedro también se conoce como "pirámide triangular".

Como todos los poliedros convexos, un tetraedro se puede plegar a partir de una sola hoja de papel. Tiene dos redes de este tipo.

Para cualquier tetraedro existe una esfera (llamada circunsfera) en la que se encuentran los cuatro vértices, y otra esfera (la inesfera) tangente a las caras del tetraedro.

Tetraedro regular

Un tetraedro regular es un tetraedro en el que las cuatro caras son triángulos equiláteros. Es uno de los cinco sólidos platónicos regulares, que se conocen desde la antigüedad.

En un tetraedro regular, todas las caras tienen el mismo tamaño y forma (congruentes) y todas las aristas tienen la misma longitud.

Cinco tetrahedra se colocan en un plano, con los puntos 3 dimensiones más altos marcados como 1, 2, 3, 4 y 5. Estos puntos se unen luego entre sí y queda un poco de espacio vacío, donde los cinco ángulos de borde no se encuentran.

Los tetraedros regulares solos no se teselan (llenan el espacio), pero si se alternan con octaedros regulares en la proporción de dos tetraedros a un octaedro, forman el panal cúbico alternado, que es un teselado. Algunos tetraedros que no son regulares, incluidos el ortosquema de Schläfli y el tetraedro de Hill, pueden formar teselados.

El tetraedro regular es autodual, lo que significa que su dual es otro tetraedro regular. La figura compuesta que comprende dos de estos tetraedros duales forma un octaedro estrellado o stella octangula.

Coordenadas de un tetraedro regular

Las siguientes coordenadas cartesianas definen los cuatro vértices de un tetraedro con longitud de arista 2, centrado en el origen y dos aristas niveladas:

{displaystyle left(pm 1,0,-{frac {1}{sqrt {2}}}right)quad {mbox{and}}quad left(0,pm 1,{frac {1}{sqrt {2}}}right)}

Expresados simétricamente como 4 puntos en la esfera unitaria, centroide en el origen, con nivel de cara inferior, los vértices son:

${displaystyle v_{1}=left({sqrt {frac {8}{9}}},0,-{frac {1}{3}}right)}$

${displaystyle v_{2}=left(-{sqrt {frac {2}{9}}},{sqrt {frac {2}{3}}},-{frac {1}{3}}right)}$

${displaystyle v_{3}=left(-{sqrt {frac {2}{9}}},-{sqrt {frac {2}{3}}},-{frac {1}{3}}right)}$

${displaystyle v_{4}=(0,0,1)}$

con la longitud del borde ${displaystyle {sqrt {frac {8}{3}}}}$ .

Otro conjunto de coordenadas se basan en un cubo alternado o demicube con longitud de borde 2. Esta forma tiene el diagrama de Coxeter y el símbolo Schläfli h{4,3}. El tetraedro en este caso tiene longitud de borde 2√2. Invertir estas coordenadas genera el tetraedro dual, y el par juntos forman el octaedro estelar, cuyos vértices son los del cubo original.

Tetraedro: (1,1,1), (1,−1,–1), (−1,–1), (−1,–1,–1,1)

Dual tetrahedron: (−1,−1,1), (−1,1), (1,−1,1), (1,1,1), (1,1,−1)

Tetraedro regular ABCD y su esfera circunscrita

Ángulos y distancias

Para un tetraedro regular de longitud de arista a:

Zona cara	${displaystyle A_{0}={frac {sqrt {3}}{4}}a^{2},}$
Superficie	$A=4,A_{0}={sqrt {3}}a^{2},$
Altura de la pirámide	${displaystyle h={frac {sqrt {6}}{3}}a={sqrt {frac {2}{3}}},a,}$
Centroide a distancia de vértice	${displaystyle {frac {3}{4}},h={frac {sqrt {6}}{4}},a={sqrt {frac {3}{8}}},a,}$
Edge a distancia de borde opuesto	${displaystyle l={frac {1}{sqrt {2}}},a,}$
Volumen	${displaystyle V={frac {1}{3}}A_{0}h={frac {sqrt {2}}{12}}a^{3}={frac {a^{3}}{6{sqrt {2}}}},}$
Ángulo de borde facial	${displaystyle arccos left({frac {1}{sqrt {3}}}right)=arctan left({sqrt {2}}right),}$ (aprox. 54.7356°)
Ángulo cara-edge, es decir, "ángulo histórico"	${displaystyle arccos left({frac {1}{3}}right)=arctan left(2{sqrt {2}}right),}$ (aprox. 70.5288°)
Ángulo Vertex-Center-Vertex, el ángulo entre líneas desde el centro de tetraedro a cualquier dos vértices. También es el ángulo entre las fronteras de Plateau en un vértice. En química se llama el ángulo de unión tetraedral. Este ángulo (en radians) es también la longitud del arco circular en la esfera de unidad resultante de proyectar centralmente un borde del tetraedro a la esfera.	${displaystyle arccos left(-{frac {1}{3}}right)=2arctan left({sqrt {2}}right),}$ (aprox. 109.4712°)
Ángulo sólido en un vértice subtenido por una cara	${displaystyle arccos left({frac {23}{27}}right)}$ (aprox. 0,5129 esteroides) (aprox. 1809.8 grados cuadrados)
Radius of circumsphere	${displaystyle R={frac {sqrt {6}}{4}}a={sqrt {frac {3}{8}}},a,}$
Radius of insphere that is tangent to faces	${displaystyle r={frac {1}{3}}R={frac {a}{sqrt {24}}},}$
Radius of midsphere that is tangent to edges	${displaystyle r_{mathrm {M} }={sqrt {rR}}={frac {a}{sqrt {8}}},}$
Radius of exspheres	${displaystyle r_{mathrm {E} }={frac {a}{sqrt {6}}},}$
Distancia al centro de esfera desde el vértice opuesto	${displaystyle d_{mathrm {VE} }={frac {sqrt {6}}{2}}a={sqrt {frac {3}{2}}}a,}$

Con respecto al plano base, la pendiente de una cara (2√2 ) es el doble de un borde (√2), correspondiente al hecho de que la distancia horizontal recorrida desde la base hasta el vértice a lo largo de una arista es el doble que a lo largo de la mediana de una cara. En otras palabras, si C es el baricentro de la base, la distancia de C a un vértice de la base es el doble que de C a el punto medio de una arista de la base. Esto se sigue del hecho de que las medianas de un triángulo se cortan en su baricentro, y este punto divide a cada uno de ellos en dos segmentos, uno de los cuales es el doble de largo que el otro (ver demostración).

Para un tetraedro regular con longitud de lado a, radio R de la esfera que lo circunscribe y distancias d_i desde un punto arbitrario en el espacio tridimensional hasta sus cuatro vértices, tenemos

{displaystyle {begin{aligned}{frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{frac {16R^{4}}{9}}&=left({frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{frac {2R^{2}}{3}}right)^{2};\4left(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}right)&=left(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}right)^{2}.end{aligned}}}

Isometrías del tetraedro regular

Las rotaciones adecuadas, (orden-3 rotación en un vértice y cara, y orden-2 en dos bordes) y plano de reflexión (a través de dos caras y un borde) en el grupo de simetría del tetraedro regular

Los vértices de un cubo se pueden agrupar en dos grupos de cuatro, cada uno formando un tetraedro regular (ver arriba, y también la animación, que muestra uno de los dos tetraedros en el cubo). Las simetrías de un tetraedro regular corresponden a la mitad de las de un cubo: las que mapean los tetraedros entre sí, y no entre sí.

El tetraedro es el único sólido platónico que no se asigna a sí mismo mediante inversión puntual.

El tetraedro regular tiene 24 isometrías, formando el grupo de simetría T_d, [3,3], (*332), isomorfo al grupo simétrico, S₄. Se pueden clasificar de la siguiente manera:

T[3,3]⁺, (332) es isomorfo al grupo alterno, A₄ (la identidad y 11 rotaciones adecuadas) con las siguientes clases de conjugación (en los paréntesis se dan las permutaciones de los vértices, o correspondientemente, las caras y la representación de la cuaternión unitaria):
- identidad (identidad; 1)
- rotación alrededor de un eje a través de un vértice, perpendicular al plano opuesto, por un ángulo de ±120°: 4 ejes, 2 por eje, juntos 8 ((1 2 3), etc. 1 ± i ± j ± k/2)
- rotación por un ángulo de 180° tal que un borde mapa al borde opuesto: 3 ((1 2)(3 4), etc. i, j, k)
reflejos en un plano perpendicular a un borde: 6
reflejos en un plano combinado con rotación de 90° sobre un eje perpendicular al plano: 3 ejes, 2 por eje, juntos 6; equivalentemente, son giros de 90° combinados con inversión (x es mapeado a −x): las rotaciones corresponden a las del cubo sobre ejes cara a cara

Proyecciones ortogonales del tetraedro regular

El tetraedro regular tiene dos proyecciones ortogonales especiales, una centrada en un vértice o de forma equivalente en una cara, y otra centrada en una arista. El primero corresponde al plano A₂ de Coxeter.

Proyección ortográfica
Centrado por	Face/vertex	Edge
Imagen
Projective simetría	[3]	[4]

Sección transversal de tetraedro regular

Una sección central de una cruz regular tetrahedron es un cuadrado.

Los dos bordes opuestos perpendiculares sesgados de un tetraedro regular definen un conjunto de planos paralelos. Cuando uno de estos planos se cruza con el tetraedro, la sección transversal resultante es un rectángulo. Cuando el plano de intersección está cerca de uno de los bordes, el rectángulo es largo y delgado. Cuando está a medio camino entre los dos bordes, la intersección es un cuadrado. La relación de aspecto del rectángulo se invierte al pasar por este punto medio. Para la intersección del cuadrado del punto medio, la línea límite resultante atraviesa todas las caras del tetraedro de manera similar. Si el tetraedro se biseca en este plano, ambas mitades se convierten en cuñas.

Un defenoide tetragonal visto ortogonalmente a los dos bordes verdes.

Esta propiedad también se aplica a los disfenoides tetragonales cuando se aplica a los dos pares de aristas especiales.

Alicatados esféricos

El tetraedro también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Proyección ortográfica	Proyección estereográfica

Apilamiento helicoidal

Un solo anillo de 30 tetraedros Boerdijk–Coxeter helix dentro de la 600 celdas, vista en proyección estereográfica

Los tetraedros regulares se pueden apilar cara a cara en una cadena aperiódica quiral llamada hélice de Boerdijk-Coxeter.

En cuatro dimensiones, todos los 4 politopos regulares convexos con celdas tetraédricas (los de 5 celdas, 16 celdas y 600 celdas) pueden construirse como mosaicos de la 3 esfera mediante estas cadenas, que se vuelven periódicas en el espacio tridimensional de la superficie límite del politopo 4.

Tetraedros irregulares

Relaciones con subgrupos de simetría tetraedral	Simetrías tetraedral mostradas en diagramas tetraedral

Los tetraedros que no tienen cuatro caras equiláteras se clasifican y nombran según las simetrías que poseen.

Si los tres pares de aristas opuestas de un tetraedro son perpendiculares, entonces se llama tetraedro ortocéntrico. Cuando solo un par de aristas opuestas son perpendiculares, se llama un tetraedro semi-ortocéntrico.

Un tetraedro isodinámico es aquel en el que las cevianas que unen los vértices a los incentros de las caras opuestas son concurrentes.

Un tetraedro isogónico tiene cevianas concurrentes que unen los vértices a los puntos de contacto de las caras opuestas con la esfera inscrita del tetraedro.

Tetraedro trirectangular

El dibujo de Kepler de un tetraedro regular inscrito en un cubo, y uno de los cuatro tetrahedra trirectangular que lo rodean, llenando el cubo.

En un tetraedro trirectangular, los tres ángulos de las caras en un vértice son ángulos rectos, como en la esquina de un cubo.

Kepler descubrió la relación entre el cubo, el tetraedro regular y el tetraedro trirectangular.

Disfenoides

Un tetraedral lleno de espacio desfenoide dentro de un cubo. Dos bordes tienen ángulos dihedral de 90°, y cuatro bordes tienen ángulos dihedral de 60°.

Un disfenoide es un tetraedro con cuatro triángulos congruentes como caras; los triángulos tienen necesariamente todos los ángulos agudos. El tetraedro regular es un caso especial de un disfenoide. Otros nombres para la misma forma incluyen bisfenoide, tetraedro isósceles y tetraedro equifacial.

Ortoesquemas

Un cubo se diseñó en seis ortoscopios característicos.

Un 3-ortosquema es un tetraedro donde las cuatro caras son triángulos rectángulos. Un ortosquema es un simplex irregular que es el casco convexo de un árbol en el que todos los bordes son mutuamente perpendiculares. En un ortosquema tridimensional, el árbol consta de tres aristas perpendiculares que conectan los cuatro vértices en una trayectoria lineal que forma dos giros en ángulo recto. El 3-ortosquema es un tetraedro que tiene dos ángulos rectos en cada uno de los dos vértices, por lo que otro nombre para él es tetraedro birectangular. También se le llama tetraedro cuadrirrectangular porque contiene cuatro ángulos rectos.

Coxeter también llama tetrahedra quadrirectangular característica tetrahedra, debido a su relación integral con los politopes regulares y sus grupos de simetría. Por ejemplo, el caso especial de un 3-orthoscheme con bordes perpendiculares de longitud igual es característico del cubo, lo que significa que el cubo puede ser subdividido en instancias de este ortoscopio. Si sus tres bordes perpendiculares son de longitud unitaria, sus bordes restantes son dos de longitud √2 y una de longitud √3, así que todos sus bordes son bordes o diagonales del cubo. El cubo puede ser disecado en seis tales 3-orthoschemes cuatro maneras diferentes, con los seis alrededor de la misma √3 cubo diagonal. El cubo también puede ser disecado en 48 más pequeño instancias de esta misma característica 3-orthoscheme (sólo de una manera, por todos sus planos de simetría a la vez). El característica tetraedro del cubo es un ejemplo de un tetraedro heroniano.

Cada politopo regular, incluyendo el tetraedro regular, tiene su ortoscopio característico. Hay un 3-orthoscheme que es el característica tetraedro del tetraedro regular. El tetraedro regular está subdividido en 24 instancias de su tetraedro característico por sus planos de simetría.

Características del tetraedro regular
	borde	arc		dihedral
l	$2$	109°28′′′	${displaystyle pi -2{text{𝜿}}}$	70°31′44′′	${displaystyle pi -2{text{𝟁}}}$

χ	${displaystyle {sqrt {tfrac {4}{3}}}approx 1.155}$	70°31′44′′	${displaystyle 2{text{𝜿}}}$	60°	${tfrac {pi }{3}}$
φ	$1$	54°44′8′′	${displaystyle {tfrac {pi }{2}}-{text{𝜿}}}$	60°	${tfrac {pi }{3}}$
↑	${displaystyle {sqrt {tfrac {1}{3}}}approx 0.577}$	54°44′8′′	${displaystyle {tfrac {pi }{2}}-{text{𝜿}}}$	60°	${tfrac {pi }{3}}$

${displaystyle _{0}R/l}$	${displaystyle {sqrt {tfrac {3}{2}}}approx 1.225}$
${displaystyle _{1}R/l}$	${displaystyle {sqrt {tfrac {1}{2}}}approx 0.707}$
${displaystyle _{2}R/l}$	${displaystyle {sqrt {tfrac {1}{6}}}approx 0.408}$

${displaystyle {text{𝜿}}}$		35°15′′	${displaystyle {tfrac {{text{arc sec }}3}{2}}}$

Si el tetraedro regular tiene longitud de borde l = 2, su característica tetraedro seis bordes tienen longitudes ${displaystyle {sqrt {tfrac {4}{3}}}}$ , $1$ , ${displaystyle {sqrt {tfrac {1}{3}}}}$ (la cara del triángulo derecho exterior, la triángulo característico χ, φ, ), más ${displaystyle {sqrt {tfrac {3}{2}}}}$ , ${displaystyle {sqrt {tfrac {1}{2}}}}$ , ${displaystyle {sqrt {tfrac {1}{6}}}}$ (edges that are the característico radii del tetraedro regular). El camino de 3 pasos a lo largo de los bordes ortogonales del ortoscopio es $1$ , ${displaystyle {sqrt {tfrac {1}{3}}}}$ , ${displaystyle {sqrt {tfrac {1}{6}}}}$ , primero desde un vértice de tetraedro a un centro de borde de tetraedro, luego girando 90° a un centro facial de tetraedro, luego girando 90° al centro de tetraedro. El ortoscheme tiene cuatro caras de triángulo derecho diferentes. La cara exterior es un triángulo de 60-90-30 que es una sexta parte de la cara de tetraedro. Las tres caras interiores al tetraedro son: un triángulo derecho con bordes $1$ , ${displaystyle {sqrt {tfrac {3}{2}}}}$ , ${displaystyle {sqrt {tfrac {1}{2}}}}$ , un triángulo derecho con bordes ${displaystyle {sqrt {tfrac {1}{3}}}}$ , ${displaystyle {sqrt {tfrac {1}{2}}}}$ , ${displaystyle {sqrt {tfrac {1}{6}}}}$ , y un triángulo derecho con bordes ${displaystyle {sqrt {tfrac {4}{3}}}}$ , ${displaystyle {sqrt {tfrac {3}{2}}}}$ , ${displaystyle {sqrt {tfrac {1}{6}}}}$ .

Tetraedros que llenan el espacio

Un tetraedro que llena el espacio se empaqueta con copias de sí mismo directamente congruentes o enantiomorfas (imagen especular) en el espacio de mosaico. El cubo se puede dividir en seis 3-ortosquemas, tres para zurdos y tres para diestros (uno de cada uno en cada cara del cubo), y los cubos pueden llenar el espacio, por lo que el 3-ortosquema característico del cubo es un espacio para llenar tetraedro en este sentido. Un disfenoide puede ser un tetraedro que llena el espacio en el sentido directamente congruente, como en el panal tetraédrico disfenoide. Sin embargo, los tetraedros regulares no pueden llenar el espacio por sí mismos.

Dominios fundamentales

Para Euclidean 3-espacio, hay 3 sencillos y relacionados Goursat tetrahedra. Se pueden ver como puntos en y dentro de un cubo.

Un tetraedro irregular que es el dominio fundamental de un grupo de simetría es un ejemplo de tetraedro de Goursat. Los tetraedros de Goursat generan todos los poliedros regulares (y muchos otros poliedros uniformes) mediante reflejos especulares, un proceso denominado construcción caleidoscópica de Wythoff.

Para los poliedros, la construcción de Wythoff dispone tres espejos en ángulo entre sí, como en un caleidoscopio. A diferencia de un caleidoscopio cilíndrico, los espejos de Wythoff están ubicados en tres caras de un tetraedro de Goursat, de modo que los tres espejos se cruzan en un solo punto.

Entre los tetraedros de Goursat que generan panales tridimensionales podemos reconocer un ortosquema (el tetraedro característico del cubo), un ortosquema doble (el tetraedro característico del cubo unido por las caras a su imagen especular) y el espacio- llenado disphenoid ilustrado arriba. El disfenoides es el ortosquema doble unido por cara a su imagen especular (un ortosquema cuádruple). Por lo tanto, los tres tetraedros de Goursat y todos los poliedros que generan por reflejos pueden dividirse en tetraedros característicos del cubo.

Isometrías de tetraedros irregulares

Las isometrías de un tetraedro irregular (sin marcar) dependen de la geometría del tetraedro, con 7 casos posibles. En cada caso se forma un grupo puntual tridimensional. Otras dos isometrías (C₃, [3]⁺), y (S₄, [2⁺, 4⁺]) puede existir si se incluye la marca de cara o borde. Se incluyen diagramas tetraédricos para cada tipo a continuación, con bordes coloreados por equivalencia isométrica, y son de color gris para bordes únicos.

Tetraedro nombre				Descripción
Simmetría
Schön.	Cox.	Orb.	Ord.
Tetraedro regular				Cuatro equilátero triángulos Forma el grupo de simetría T_d, isomorfa al grupo simétrico, S₄. Un tetraedro regular tiene diagrama de Coxeter y el símbolo Schläfli {3,3}.
T_d T	[3,3] [3,3]⁺	*332 332	24 12
pirámide triangular				An equilátero base triangular y tres iguales isosceles laterales triángulo Da 6 isometries, correspondientes a las 6 isometries de la base. Como permutaciones de los vértices, estas 6 isometrias son la identidad 1, (123), (132), (12), (13) y (23), formando el grupo de simetría C_3v, isomorfa al grupo simétrico, S₃. Una pirámide triangular tiene el símbolo Schläfli {3} Máxima().
C_3v C₃	[3] [3]⁺	*33 33	6 3
Espenoide espejo				Dos iguales b) triángulos con un borde base común Esto tiene dos pares de bordes iguales (1,3), (1,4) y (2,3), (2,4) y de otro modo ningún borde igual. Las únicas dos isometrías son 1 y la reflexión (34), dando al grupo C_s, también isomorfa al grupo cíclico, Z₂.
C_s =C_1h =C_1v	[ ]	*	2
Tetraedro irregular (Sin simetría)				Cuatro triángulos desiguales Su única isometría es la identidad, y el grupo de simetría es el grupo trivial. Un tetraedro irregular tiene el símbolo Schläfli () Diccionario()
C₁	[ ]⁺	1	1
Disphenoids (Cuatro triángulos iguales)
Tetragonal disphenoid				Cuatro iguales isosceles triángulos Tiene 8 isometrías. Si los bordes (1,2) y (3,4) son de diferente longitud a los otros 4, entonces las 8 isometrías son la identidad 1, reflexiones (12) y (34), y 180° rotaciones (12)(34), (13)(24), (14)(23) e inadecuadas rotaciónes de 90° (1234) y (1432) formando el grupo de simetría D_2d. Un defenoide tetragonal tiene el diagrama de Coxeter y el símbolo Schläfli s{2,4}.
D_2d S₄	[2]⁺,4] [2]⁺,4⁺]	2*2 2×	8 4
Defenoide Rómbico				Cuatro iguales b) triángulos Tiene 4 isometrías. Las isometrías son 1 y 180° de rotación (12)(34), (13)(24), (14)(23). Este es el grupo Klein V₄ o Z₂², presente como el grupo de puntos D₂. Un defenoide rhombic tiene diagrama de Coxeter y el símbolo Schläfli sr{2,2}.
D₂	[2,2]⁺	222	4
Disfenoides generalizados (2 pares de triángulos iguales)
Disphenoid digonal				Dos pares de iguales isosceles triángulos Esto da dos bordes opuestos (1,2) y (3,4) que son perpendiculares pero diferentes longitudes, y luego las 4 isometrías son 1, reflejos (12) y (34) y la rotación de 180° (12)(34). El grupo de simetría es C_2v, isomorfa a los cuatro grupos Klein V₄. Un defenoide digonal tiene el símbolo Schläfli { } Máxima{ }.
C_2v C₂	[2] [2]⁺	*22 22	4 2
Defenoide folílico				Dos pares de iguales b) o isosceles triángulos Esto tiene dos pares de bordes iguales (1,3), (2,4) y (1,4), (2,3) pero de lo contrario no hay bordes iguales. Las únicas dos isometrías son 1 y la rotación (12)(34), dando al grupo C₂ isomorfa al grupo cíclico, Z₂.
C₂	[2]⁺	22	2

Propiedades generales

Volumen

El volumen de un tetraedro viene dado por la fórmula del volumen de la pirámide:

{displaystyle V={frac {1}{3}}A_{0},h,}

donde A₀ es el área de la base y h es la altura desde la base hasta el vértice. Esto se aplica a cada una de las cuatro elecciones de la base, por lo que las distancias desde los vértices a las caras opuestas son inversamente proporcionales a las áreas de estas caras.

Para un tetraedro con vértices a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), c = (c₁, c₂, c₃), y d = (d₁, d₂, d₃), el volumen es 1/6|det( a - d, b - d, c - d)|, o cualquier otra combinación de pares de vértices que formen un grafo simplemente conexo. Esto se puede reescribir usando un producto escalar y un producto vectorial, dando como resultado

V={frac {|(mathbf {a} -mathbf {d})cdot ((mathbf {b} -mathbf {d})times (mathbf {c} -mathbf {d}))|}{6}}.

Si se elige que el origen del sistema de coordenadas coincida con el vértice d, entonces d = 0, por lo que

V={frac {|mathbf {a} cdot (mathbf {b} times mathbf {c})|}{6}},

donde a, b y c representan tres aristas que se encuentran en un vértice, y a · (b × c) es un triple producto escalar. Comparando esta fórmula con la utilizada para calcular el volumen de un paralelepípedo, concluimos que el volumen de un tetraedro es igual a 1/6 del volumen de cualquier paralelepípedo que comparta tres aristas convergentes con él.

El valor absoluto del producto triple escalar se puede representar como los siguientes valores absolutos de determinantes:

6cdot V={begin{Vmatrix}mathbf {a} &mathbf {b} &mathbf {c} end{Vmatrix}}

6cdot V={begin{Vmatrix}mathbf {a} \mathbf {b} \mathbf {c} end{Vmatrix}}

Donde

{displaystyle {begin{cases}mathbf {a} =(a_{1},a_{2},a_{3}),\mathbf {b} =(b_{1},b_{2},b_{3}),\mathbf {c} =(c_{1},c_{2},c_{3}),end{cases}}}

se expresan como vectores de fila o columna.

Por lo tanto

36cdot V^{2}={begin{vmatrix}mathbf {a^{2}} &mathbf {a} cdot mathbf {b} &mathbf {a} cdot mathbf {c} \mathbf {a} cdot mathbf {b} &mathbf {b^{2}} &mathbf {b} cdot mathbf {c} \mathbf {a} cdot mathbf {c} &mathbf {b} cdot mathbf {c} &mathbf {c^{2}} end{vmatrix}}

Donde

{displaystyle {begin{cases}mathbf {a} cdot mathbf {b} =abcos {gamma },\mathbf {b} cdot mathbf {c} =bccos {alpha },\mathbf {a} cdot mathbf {c} =accos {beta }.end{cases}}}

que da

V={frac {abc}{6}}{sqrt {1+2cos {alpha }cos {beta }cos {gamma }-cos ^{2}{alpha }-cos ^{2}{beta }-cos ^{2}{gamma }}},,

donde α, β, γ son los ángulos planos que ocurren en el vértice d. El ángulo α, es el ángulo entre las dos aristas que conectan el vértice d con los vértices b y c. El ángulo β, lo hace por los vértices a y c, mientras que γ, está definido por la posición de los vértices a y b.

Si no requerimos que d = 0 entonces

{displaystyle 6cdot V=left|det left({begin{matrix}a_{1}&b_{1}&c_{1}&d_{1}\a_{2}&b_{2}&c_{2}&d_{2}\a_{3}&b_{3}&c_{3}&d_{3}\1&1&1&1end{matrix}}right)right|,.}

Dadas las distancias entre los vértices de un tetraedro, el volumen se puede calcular utilizando el determinante de Cayley-Menger:

288cdot V^{2}={begin{vmatrix}0&1&1&1&1\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0end{vmatrix}}

donde los subíndices i, j ∈ {1, 2, 3, 4} representan los vértices {a, b, c, d} y d_ij es la distancia por pares entre ellos, es decir, la longitud del borde que conecta los dos vértices. Un valor negativo del determinante significa que no se puede construir un tetraedro con las distancias dadas. Esta fórmula, a veces llamada fórmula de Tartaglia, se debe esencialmente al pintor Piero della Francesca en el siglo XV, como un análogo tridimensional de la fórmula de Heron del siglo I para el área de un triángulo.

Sean $a, b, c$ tres aristas que se unen en un punto, y $x, y, z$ los bordes opuestos. Sea $V$ el volumen del tetraedro; después

{displaystyle V={frac {sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}}{12}}}

dónde

{displaystyle {begin{aligned}X&=b^{2}+c^{2}-x^{2},\Y&=a^{2}+c^{2}-y^{2},\Z&=a^{2}+b^{2}-z^{2}.end{aligned}}}

La fórmula anterior usa seis longitudes de aristas, y la siguiente fórmula usa tres longitudes de aristas y tres ángulos.

{displaystyle V={frac {abc}{6}}{sqrt {1+2cos {alpha }cos {beta }cos {gamma }-cos ^{2}{alpha }-cos ^{2}{beta }-cos ^{2}{gamma }}}}

Fórmula tipo Heron para el volumen de un tetraedro

Seis linduras de Tetraedro

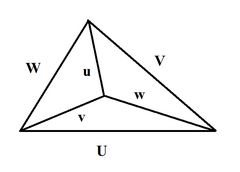
Si $U$ , $V$ , $W$ , $u$ , $v$ , $w$ son las longitudes de las aristas del tetraedro (los tres primeros forman un triángulo; con $u$ opuesto a $U$ , $v$ opuesto a $V$ , $w$ opuesto a $W$ ), luego

{displaystyle V={frac {sqrt {,(-p+q+r+s),(p-q+r+s),(p+q-r+s),(p+q+r-s)}}{192,u,v,w}}}

dónde

{displaystyle {begin{aligned}p&={sqrt {xYZ}},&q&={sqrt {yZX}},&r&={sqrt {zXY}},&s&={sqrt {xyz}},end{aligned}}}

{displaystyle {begin{aligned}X&=(w-U+v),(U+v+w),&x&=(U-v+w),(v-w+U),\Y&=(u-V+w),(V+w+u),&y&=(V-w+u),(w-u+V),\Z&=(v-W+u),(W+u+v),&z&=(W-u+v),(u-v+W).end{aligned}}}

Divisor de volumen

Cualquier plano que contenga una bimediana (conector de aristas opuestas & puntos medios) de un tetraedro biseca el volumen del tetraedro.

Volumen no euclidiano

Para tetraedros en espacio hiperbólico o en geometría elíptica tridimensional, los ángulos diedros del tetraedro determinan su forma y, por lo tanto, su volumen. En estos casos, el volumen viene dado por la fórmula de Murakami-Yano. Sin embargo, en el espacio euclidiano, escalar un tetraedro cambia su volumen pero no sus ángulos diedros, por lo que no puede existir tal fórmula.

Distancia entre los bordes

Dos aristas opuestas cualesquiera de un tetraedro se encuentran en dos líneas oblicuas, y la distancia entre las aristas se define como la distancia entre las dos líneas oblicuas. Sea d la distancia entre las líneas oblicuas formadas por los bordes opuestos a y b − c como se calcula aquí. Entonces otra fórmula de volumen está dada por

V={frac {d|(mathbf {a} times mathbf {(b-c)})|}{6}}.

Propiedades análogas a las de un triángulo

El tetraedro tiene muchas propiedades análogas a las de un triángulo, incluidas una insfera, una circunsfera, un tetraedro medio y una exsfera. Tiene centros respectivos como incentro, circuncentro, excentros, centro de Spieker y puntos como un centroide. Sin embargo, generalmente no hay ortocentro en el sentido de altitudes que se cruzan.

Gaspard Monge encontró un centro que existe en cada tetraedro, ahora conocido como el punto de Monge: el punto donde se cruzan los seis planos medios de un tetraedro. Un plano medio se define como un plano que es ortogonal a un borde que une dos vértices cualesquiera y que también contiene el centroide de un borde opuesto formado al unir los otros dos vértices. Si las altitudes del tetraedro se cruzan, entonces el punto de Monge y el ortocentro coinciden para dar la clase de tetraedro ortocéntrico.

Una línea ortogonal caída desde el punto Monge a cualquier cara se encuentra con esa cara en el punto medio del segmento de línea entre el ortocentro de esa cara y el pie de la altura caída desde el vértice opuesto.

Un segmento de recta que une un vértice de un tetraedro con el baricentro de la cara opuesta se llama mediana y un segmento de recta que une los puntos medios de dos aristas opuestas se llama bimediana del tetraedro. Por lo tanto, hay cuatro medianas y tres bimedianas en un tetraedro. Estos siete segmentos de recta son todos concurrentes en un punto llamado centroide del tetraedro. Además, las cuatro medianas se dividen en una proporción de 3:1 por el centroide (ver el teorema de Commandino). El baricentro de un tetraedro es el punto medio entre su punto Monge y el circuncentro. Estos puntos definen la línea de Euler del tetraedro que es análoga a la línea de Euler de un triángulo.

El círculo de nueve puntos del triángulo general tiene un análogo en la circunsfera del tetraedro medio de un tetraedro. Es la esfera de doce puntos y además de los centroides de las cuatro caras del tetraedro de referencia, pasa por cuatro puntos de Euler sustitutos, a un tercio del camino desde el Monge apuntar hacia cada uno de los cuatro vértices. Finalmente pasa por los cuatro puntos base de las rectas ortogonales caídas desde cada punto de Euler hasta la cara que no contiene el vértice que generó el punto de Euler.

El centro T de la esfera de doce puntos también se encuentra en la línea de Euler. A diferencia de su contraparte triangular, este centro se encuentra a un tercio del camino desde el punto M de Monge hacia el circuncentro. Además, una línea ortogonal a través de T a una cara elegida es coplanar con otras dos líneas ortogonales a la misma cara. La primera es una línea ortogonal que pasa por el punto de Euler correspondiente a la cara elegida. La segunda es una línea ortogonal que pasa por el baricentro de la cara elegida. Esta línea ortogonal a través del centro de doce puntos se encuentra a medio camino entre la línea ortogonal del punto de Euler y la línea ortogonal centroidal. Además, para cualquier cara, el centro de doce puntos se encuentra en el punto medio del punto de Euler correspondiente y el ortocentro de esa cara.

El radio de la esfera de doce puntos es un tercio del circunradio del tetraedro de referencia.

Existe una relación entre los ángulos formados por las caras de un tetraedro general dada por

{begin{vmatrix}-1&cos {(alpha _{12})}&cos {(alpha _{13})}&cos {(alpha _{14})}\cos {(alpha _{12})}&-1&cos {(alpha _{23})}&cos {(alpha _{24})}\cos {(alpha _{13})}&cos {(alpha _{23})}&-1&cos {(alpha _{34})}\cos {(alpha _{14})}&cos {(alpha _{24})}&cos {(alpha _{34})}&-1\end{vmatrix}}=0,

donde α_ij es el ángulo entre las caras i y j.

La mediana geométrica de las coordenadas de posición del vértice de un tetraedro y su centro isogónico están asociadas, en circunstancias análogas a las observadas para un triángulo. Lorenz Lindelöf encontró que, correspondiente a cualquier tetraedro dado, hay un punto ahora conocido como centro isogónico, O, en el cual los ángulos sólidos subtendidos por las caras son iguales, teniendo un valor común de π sr, y en el que los ángulos subtendidos por los lados opuestos son iguales. Un ángulo sólido de π sr es un cuarto del subtendido por todo el espacio. Cuando todos los ángulos sólidos en los vértices de un tetraedro son menores que π sr, O está dentro del tetraedro, y debido a que la suma de las distancias desde O a los vértices es un mínimo, O coincide con la mediana geométrica, M, de los vértices. En el caso de que el ángulo sólido en uno de los vértices, v, mida exactamente π sr, entonces O y M coinciden con v. Sin embargo, si un tetraedro tiene un vértice, v, con un ángulo sólido mayor que π sr, M todavía corresponde a v, pero O se encuentra fuera del tetraedro.

Relaciones geométricas

Un tetraedro es un 3-simplex. A diferencia del caso de los demás sólidos platónicos, todos los vértices de un tetraedro regular son equidistantes entre sí (son la única disposición posible de cuatro puntos equidistantes en el espacio tridimensional).

Un tetraedro es una pirámide triangular y el tetraedro regular es autodual.

Un tetraedro regular se puede incrustar dentro de un cubo de dos maneras, de modo que cada vértice sea un vértice del cubo y cada arista sea una diagonal de una de las caras del cubo. Para una de estas incrustaciones, las coordenadas cartesianas de los vértices son

(+1, +1, +1);

(1, - 1, +1);

(1, +1, -1);

(+1, −1, −1).

Esto produce un tetraedro con longitud de borde 2√2, centrado en el origen. Para el otro tetraedro (que es dual al primero), invierta todos los signos. Estos dos vértices de tetraedros combinados son los vértices de un cubo, lo que demuestra que el tetraedro regular es el 3-semicubo.

La estela octangula.

El volumen de este tetraedro es un tercio del volumen del cubo. La combinación de ambos tetraedros da un compuesto poliédrico regular llamado compuesto de dos tetraedros o stella octangula.

El interior de la stella octangula es un octaedro y, en consecuencia, un octaedro regular es el resultado de cortar, de un tetraedro regular, cuatro tetraedros regulares de la mitad del tamaño lineal (es decir, rectificar el tetraedro).

La incrustación anterior divide el cubo en cinco tetraedros, uno de los cuales es regular. De hecho, cinco es el número mínimo de tetraedros necesarios para componer un cubo. Para ver esto, partiendo de un tetraedro base con 4 vértices, cada tetraedro agregado agrega como máximo 1 vértice nuevo, por lo que se deben agregar al menos 4 más para hacer un cubo, que tiene 8 vértices.

Al inscribir tetraedros dentro del compuesto regular de cinco cubos se obtienen dos compuestos regulares más, que contienen cinco y diez tetraedros.

Los tetraedros regulares no pueden teselar el espacio por sí mismos, aunque este resultado parece lo suficientemente probable como para que Aristóteles afirmara que era posible. Sin embargo, dos tetraedros regulares se pueden combinar con un octaedro, dando un romboedro que puede teselar el espacio como el panal tetraédrico-octaédrico.

Sin embargo, se conocen varios tetraedros irregulares, cuyas copias pueden teselar el espacio, por ejemplo, el ortoesquema característico del cubo y el disfenoide del panal tetraédrico disfenoide. La lista completa sigue siendo un problema abierto.

Si se relaja el requisito de que todos los tetraedros tengan la misma forma, se puede teselar el espacio usando solo tetraedros de muchas maneras diferentes. Por ejemplo, se puede dividir un octaedro en cuatro tetraedros idénticos y combinarlos nuevamente con dos regulares. (Como nota al margen: estos dos tipos de tetraedro tienen el mismo volumen).

El tetraedro es único entre los poliedros uniformes porque no posee caras paralelas.

Una ley de senos para tetraedros y el espacio de todas las formas de tetraedros

Un corolario de la ley habitual de los senos es que en un tetraedro con vértices O, A, B, C, tenemos

sin angle OABcdot sin angle OBCcdot sin angle OCA=sin angle OACcdot sin angle OCBcdot sin angle OBA.,

Uno puede ver los dos lados de esta identidad como correspondientes a las orientaciones de la superficie en sentido horario y antihorario.

Poner cualquiera de los cuatro vértices en el papel de O produce cuatro de esas identidades, pero como máximo tres de ellas son independientes: si el "en el sentido de las agujas del reloj" los lados de tres de ellos se multiplican y se deduce que el producto es igual al producto de los "en sentido antihorario" lados de las mismas tres identidades, y luego se cancelan los factores comunes de ambos lados, el resultado es la cuarta identidad.

Tres ángulos son los ángulos de algún triángulo si y solo si su suma es 180° (π radianes). ¿Qué condición sobre 12 ángulos es necesaria y suficiente para que sean los 12 ángulos de algún tetraedro? Claramente, la suma de los ángulos de cualquier lado del tetraedro debe ser 180°. Dado que hay cuatro triángulos de este tipo, existen cuatro restricciones de este tipo sobre las sumas de los ángulos y, por lo tanto, el número de grados de libertad se reduce de 12 a 8. Las cuatro relaciones dadas por esta ley del seno reducen aún más el número de grados de libertad, de 8 hasta no 4 sino 5, ya que la cuarta restricción no es independiente de las tres primeras. Por lo tanto, el espacio de todas las formas de tetraedros es de 5 dimensiones.

Ley de cosenos para tetraedros

Sea {P₁P₂, P ₃, P₄} sean las puntas de un tetraedro. Sea Δ_i el área de la cara opuesta al vértice P_i y sea θ_ij el ángulo diedro entre las dos caras del tetraedro adyacentes a la arista P_iP_j.

La ley de los cosenos para este tetraedro, que relaciona las áreas de las caras del tetraedro con los ángulos diedros alrededor de un vértice, viene dada por la siguiente relación:

Delta _{i}^{2}=Delta _{j}^{2}+Delta _{k}^{2}+Delta _{l}^{2}-2(Delta _{j}Delta _{k}cos theta _{il}+Delta _{j}Delta _{l}cos theta _{ik}+Delta _{k}Delta _{l}cos theta _{ij})

Punto interior

Sea P cualquier punto interior de un tetraedro de volumen V cuyos vértices son A, B, C y D, y para las cuales las áreas de las caras opuestas son F_a, F_b, F_c y F_d. Después

{displaystyle PAcdot F_{mathrm {a} }+PBcdot F_{mathrm {b} }+PCcdot F_{mathrm {c} }+PDcdot F_{mathrm {d} }geq 9V.}

Para los vértices A, B, C y D, punto interior P, y los pies J, K, L y M de las perpendiculares desde P a las caras, y supongamos que las caras tienen áreas iguales, entonces

PA+PB+PC+PDgeq 3(PJ+PK+PL+PM).

Inradio

Denotando el interior del radio de un tetraedro como r y el interior del radio de sus caras triangulares como r_i para i = 1, 2, 3, 4, tenemos

{frac {1}{r_{1}^{2}}}+{frac {1}{r_{2}^{2}}}+{frac {1}{r_{3}^{2}}}+{frac {1}{r_{4}^{2}}}leq {frac {2}{r^{2}}},

con igualdad si y solo si el tetraedro es regular.

Si A₁, A₂, A₃ y A₄ indican el área de cada cara, el valor de r viene dado por

{displaystyle r={frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}}

Esta fórmula se obtiene de dividir el tetraedro en cuatro tetrahedra cuyos puntos son los tres puntos de uno de los rostros originales y el incentivo. Desde que los cuatro subtetrahedra llenan el volumen, tenemos ${displaystyle V={frac {1}{3}}A_{1}r+{frac {1}{3}}A_{2}r+{frac {1}{3}}A_{3}r+{frac {1}{3}}A_{4}r}$ .

Circunferencia

Denote el circunradio de un tetraedro como R. Sean a, b, c las longitudes de las tres aristas que se unen en un vértice, y A, B, C la longitud de los bordes opuestos. Sea V el volumen del tetraedro. Después

{displaystyle R={frac {sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.}

Circuncentro

El circuncentro de un tetraedro se puede encontrar como la intersección de tres planos bisectores. Un plano bisector se define como el plano centrado y ortogonal a un borde del tetraedro. Con esta definición, el circuncentro $C$ de un tetraedro con vértices $x 0$ , $x 1$ , $x 2$ , $x 3$ se puede formular como producto matriz-vector:

{displaystyle {begin{aligned}C&=A^{-1}B&{text{where}}& &A=left({begin{matrix}left[x_{1}-x_{0}right]^{T}\left[x_{2}-x_{0}right]^{T}\left[x_{3}-x_{0}right]^{T}end{matrix}}right)& &{text{and}}& &B={frac {1}{2}}left({begin{matrix}|x_{1}|^{2}-|x_{0}|^{2}\|x_{2}|^{2}-|x_{0}|^{2}\|x_{3}|^{2}-|x_{0}|^{2}end{matrix}}right)\end{aligned}}}

A diferencia del centroide, es posible que el circuncentro no siempre se encuentre en el interior de un tetraedro. Análogamente a un triángulo obtuso, el circuncentro está fuera del objeto para un tetraedro obtuso.

Centroide

El centro de masa del tetraedro se calcula como la media aritmética de sus cuatro vértices, consulte Centroide.

Caras

La suma de las áreas de tres caras cualesquiera es mayor que el área de la cuarta cara.

Tetrahedra entera

(feminine)

Existen tetraedros que tienen longitudes de borde, áreas de cara y volumen con valores enteros. Estos se llaman tetraedros heronianos. Un ejemplo tiene un borde de 896, el borde opuesto de 990 y los otros cuatro bordes de 1073; dos caras son triángulos isósceles con áreas de 436800 y los otros dos son isósceles con áreas de 47120, mientras que el volumen es 124185600.

Un tetraedro puede tener un volumen entero y enteros consecutivos como aristas, siendo un ejemplo el que tiene las aristas 6, 7, 8, 9, 10 y 11 y el volumen 48.

Poliedros y compuestos relacionados

Un tetraedro regular puede verse como una pirámide triangular.

pirámides regulares
Digonal	Triangular	Plaza	Pentagonal	Hexagonal	Heptagonal	Octagonal	Enneagonal	Decagonal...
Impropio	Recursos ordinarios	Equilateral		Isosceles

Un tetraedro regular puede verse como un poliedro degenerado, un antiprisma digonal uniforme, donde los polígonos base son digones reducidos.

Familia de uniforme n- antiprismos pasados
v
t
e
Nombre del Antiprismo	Antiprismos digonal	(Trigonal) Antiprismos triangular	(Tetragonal) Antiprisma cuadrado	Antiprisma pentagonal	Antiprisma hexagonal	Antiprismos heptagonal	Antiprisma Octagonal	Antiprisma enneagonal	Antiprisma Decagonal	Antiprisma hendecagonal	Antiprisma dodecagonal	...	Apeirogonal antiprisma
Imagen de poliedro												...
Imagen de revestimiento esférico												Imagen de azulado plano
Config de Vertex.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Un tetraedro regular puede verse como un poliedro degenerado, un trapezoedro digonal dual uniforme, que contiene 6 vértices, en dos conjuntos de aristas colineales.

Familia de n- trampa mortal
Nombre de Trapezohedron	Digonal trapezohedron (Tetraedro)	Trigonal trapezohedron	Tetragonal trapezohedron	Pentagonal trapezohedron	Hexagonal trapezohedron	Heptagonal trapezohedron	trapezohedro Octagonal	Decagonal trapezohedron	Dodecagonal trapezohedron	...	Apeirogonal trapezohedron
Imagen de poliedro										...
Imagen de revestimiento esférico										Imagen de azulado plano
Configuración facial	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V dieta.3.3.3

Un proceso de truncamiento aplicado al tetraedro produce una serie de poliedros uniformes. Truncar los bordes hasta los puntos produce el octaedro como un tetraedro rectificado. El proceso se completa como una birectificación, reduciendo las caras originales a puntos y produciendo el tetraedro autodual una vez más.

Familia de polihedra de tetraedral uniforme
Simetría: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros regulares con los símbolos de Schläfli {3,n}, continuando en el plano hiperbólico.

*n32 mutación simetría de los revestimientos regulares: {3}n} v t e
Spherical				Euclid.	Hipersión compacta.		Paraco.	Hiperbólico no consumado

3.3	33	34	35	36	37	38	3 mujeres	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

El tetraedro está topológicamente relacionado con una serie de poliedros regulares y mosaicos con figuras de vértice de orden 3.

*n32 mutación simetría de los revestimientos regulares: {}n,3} v t e
Spherical				Euclidean	Hiperb compacto.		Paraco.	Hiperbólico no consumado

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	- ¿Qué?	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Compuestos de tetrahedra
Dos tetrahedra en un cubo
Compuesto de cinco tetrahedra
Compuesto de diez tetrahedra

Se puede construir un poliedro interesante a partir de cinco tetraedros que se cruzan. Este compuesto de cinco tetraedros se conoce desde hace cientos de años. Aparece regularmente en el mundo del origami. Uniendo los veinte vértices formaría un dodecaedro regular. Hay formas tanto para zurdos como para diestros, que son imágenes especulares entre sí. La superposición de ambas formas da un compuesto de diez tetraedros, en el que los diez tetraedros están dispuestos como cinco pares de stellae octangulae. Una stella octangula es un compuesto de dos tetraedros en posición dual y sus ocho vértices definen un cubo como su casco convexo.

El hosoedro cuadrado es otro poliedro de cuatro caras, pero no tiene caras triangulares.

El poliedro de Szilassi y el tetraedro son los dos únicos poliedros conocidos en los que cada cara comparte una arista entre sí. Además, el poliedro de Császár (en sí mismo es el dual del poliedro de Szilassi) y el tetraedro son los dos únicos poliedros conocidos en los que cada diagonal se encuentra en los lados.

Aplicaciones

Análisis numérico

Un volumen irregular en el espacio puede ser aproximado por una superficie irregular triangulada, y elementos irregulares de volumen tetraedral.

En el análisis numérico, las formas tridimensionales complicadas suelen descomponerse o aproximarse mediante una malla poligonal de tetraedros irregulares en el proceso de establecer las ecuaciones para el análisis de elementos finitos, especialmente en la solución numérica de ecuaciones diferenciales parciales. Estos métodos tienen amplias aplicaciones en aplicaciones prácticas en dinámica de fluidos computacional, aerodinámica, campos electromagnéticos, ingeniería civil, ingeniería química, arquitectura e ingeniería naval y campos relacionados.

Ingeniería estructural

Un tetraedro que tiene bordes rígidos es inherentemente rígido. Por esta razón, a menudo se utiliza para reforzar las estructuras de marcos, como los marcos espaciales.

Aviación

En algunos aeródromos, un marco grande en forma de tetraedro con dos lados cubiertos con un material delgado está montado sobre un pivote giratorio y siempre apunta hacia el viento. Está construido lo suficientemente grande como para ser visto desde el aire y, a veces, está iluminado. Su finalidad es servir de referencia a los pilotos indicando la dirección del viento.

Química

El iión de amonio es tetraedral

Cálculo del ángulo central con un producto de punto

La forma de tetraedro se ve en la naturaleza en moléculas unidas covalentemente. Todos los átomos con hibridación sp3 están rodeados por átomos (o pares de electrones solitarios) en las cuatro esquinas de un tetraedro. Por ejemplo, en una molécula de metano (CH
₄) o un ion de amonio (NH⁺
₄), cuatro átomos de hidrógeno rodean un átomo central de carbono o nitrógeno con simetría tetraédrica. Por esta razón, una de las revistas líderes en química orgánica se llama Tetrahedron. El ángulo central entre dos vértices cualesquiera de un tetraedro perfecto es arccos(−1/3), o aproximadamente 109,47°.

Agua, H
₂O, también tiene una estructura tetraédrica, con dos átomos de hidrógeno y dos pares de electrones solitarios alrededor los átomos centrales de oxígeno. Sin embargo, su simetría tetraédrica no es perfecta porque los pares solitarios se repelen más que los enlaces O-H simples.

Los diagramas de fase cuaternaria de mezclas de sustancias químicas se representan gráficamente como tetraedros.

Sin embargo, los diagramas de fase cuaternarios en ingeniería de comunicaciones se representan gráficamente en un plano bidimensional.

Electricidad y electrónica

Si se sueldan seis resistencias iguales para formar un tetraedro, entonces la resistencia medida entre dos vértices cualesquiera es la mitad de la de una resistencia.

Dado que el silicio es el semiconductor más común utilizado en la electrónica de estado sólido, y el silicio tiene una valencia de cuatro, la forma tetraédrica de los cuatro enlaces químicos en el silicio tiene una fuerte influencia en cómo se forman los cristales de silicio y qué formas asumen..

Espacio de color

Los tetraedros se utilizan en algoritmos de conversión de espacio de color específicamente para casos en los que el eje de luminancia segmenta diagonalmente el espacio de color (por ejemplo, RGB, CMY).

Juegos

dados de 4 caras

El Juego Real de Ur, que data del 2600 a. C., se jugaba con un juego de dados tetraédricos.

Especialmente en los juegos de rol, este sólido se conoce como dado de 4 caras, uno de los dados poliédricos más comunes, con el número que aparece alrededor de la parte inferior o en el vértice superior. Algunos rompecabezas tipo cubo de Rubik son tetraédricos, como Pyraminx y Pyramorphix.

Geología

La hipótesis tetraédrica, publicada originalmente por William Lowthian Green para explicar la formación de la Tierra, fue popular a principios del siglo XX.

Cultura popular

Stanley Kubrick originalmente pretendía que el monolito en 2001: A Space Odyssey fuera un tetraedro, según Marvin Minsky, un científico cognitivo y experto en inteligencia artificial que asesoró a Kubrick en la computadora HAL 9000 y otros aspectos de la película. Kubrick descartó la idea de usar el tetraedro porque un visitante que vio imágenes de él no reconoció lo que era y no quería nada en la película que la gente común no entendiera.

Gráfico tetraédrico

El esqueleto del tetraedro (que comprende los vértices y las aristas) forma un gráfico, con 4 vértices y 6 aristas. Es un caso especial del gráfico completo, K₄, y gráfico de rueda, W₄. Es uno de los 5 gráficos platónicos, cada uno un esqueleto de su sólido platónico.

Simetría 3 veces

Contenido relacionado

Más resultados...