Teodoro de Cirene

Teodoro de Cirene (griego: Θεόδωρος ὁ Κυρηναῖος) fue un matemático griego antiguo que vivió durante el siglo V a.C. Los únicos relatos de primera mano que se conservan de él se encuentran en tres de los diálogos de Platón: el Teeteto, el Sofista y el Estadista. En el diálogo anterior, plantea una construcción matemática ahora conocida como la Espiral de Teodoro.

Vida

Poco se conoce como Theodorus' biografía más allá de lo que se puede inferir de los diálogos de Platón. Nació en la colonia de Cirene, en el norte de África, y aparentemente enseñó tanto allí como en Atenas. Se queja de vejez en el Teeteto, cuya dramática fecha del 399 a. C. sugiere que su período de florecimiento se produjo a mediados del siglo V. El texto también lo asocia con el sofista Protágoras, con quien afirma haber estudiado antes de dedicarse a la geometría. Una dudosa tradición repetida entre biógrafos antiguos como Diógenes Laercio sostenía que Platón estudió más tarde con él en Cirene, Libia. Este eminente matemático Teodoro fue, junto con Alcibíades y muchos otros matemáticos de Sócrates, compañeros (muchos de los cuales estarían asociados con los Treinta Tiranos), acusados de distribuir los misterios en un simposio, según Plutarco, quien era sacerdote del templo de Delfos.

Trabajar en matemáticas

Teodoro' La obra se conoce a través de un único teorema, que se presenta en el contexto literario del Teeteto y se ha argumentado alternativamente como históricamente exacto o ficticio. En el texto, su alumno Teeteto le atribuye el teorema de que las raíces cuadradas de los números no cuadrados hasta 17 son irracionales:

Theodorus aquí estaba dibujando algunas figuras para nosotros en la ilustración de las raíces, mostrando que los cuadrados que contienen tres pies cuadrados y cinco pies cuadrados no son proporcionables en longitud con la unidad del pie, y por lo tanto, seleccionando cada uno en su turno hasta la plaza que contiene diecisiete pies cuadrados y en que se detuvo.

El cuadrado que contiene dos. unidades cuadradas no se menciona, tal vez porque la incommensurabilidad de su lado con la unidad ya era conocida.) El método de prueba de Theodorus no se conoce. Ni siquiera se sabe si, en el pasaje citado, "hasta" (μ Conceptχρι) significa que se incluye diecisiete. Si diecisiete está excluido, la prueba de Theodorus puede haber dependido simplemente de considerar si los números son iguales o extraños. De hecho, Hardy y Wright y Knorr sugiere pruebas que dependen en última instancia del siguiente teorema: Si x2=nSí.2{displaystyle ¿Qué? es soluble en enteros, y n{displaystyle n} es extraño, entonces n{displaystyle n} debe ser congruente con 1 modulo 8 (desde x{displaystyle x} y Sí.{displaystyle y} puede ser asumido extraño, por lo que sus cuadrados son congruentes a 1 modulo 8.

Que no se puede probar la irracionalidad la raíz cuadrada de 17 por consideraciones restringidas a la aritmética de la incluso y la extraña se ha mostrado en un sistema de la aritmética de la incluso y la extraña en y, pero es un problema abierto en un sistema de axioma natural más fuerte para la aritmética de la incluso y la rareza

Una posibilidad sugerida anteriormente por Zeuthen es que Teodoro aplicó el llamado algoritmo euclidiano, formulado en la Proposición X.2 de los Elementos como prueba de inconmensurabilidad. En términos modernos, el teorema es que un número real con una expansión fraccional continua infinita es irracional. Las raíces cuadradas irracionales tienen expansiones periódicas. El período de la raíz cuadrada de 19 tiene una longitud de 6, que es mayor que el período de la raíz cuadrada de cualquier número menor. El período de √17 tiene longitud uno (también la tiene √18; pero la irracionalidad de √18 se sigue de la de √2).

La llamada Espiral de Teodoro está compuesta por triángulos rectángulos contiguos con longitudes de hipotenusa iguales √2, √3, √4,…, √17; los triángulos adicionales hacen que el diagrama se superponga. Philip J. Davis interpoló los vértices de la espiral para obtener una curva continua. Analiza la historia de los intentos de determinar la identidad de Teodoro. método en su libro Espirales: De Theodorus al Caos, y hace breves referencias al asunto en su serie ficticia Thomas Gray.

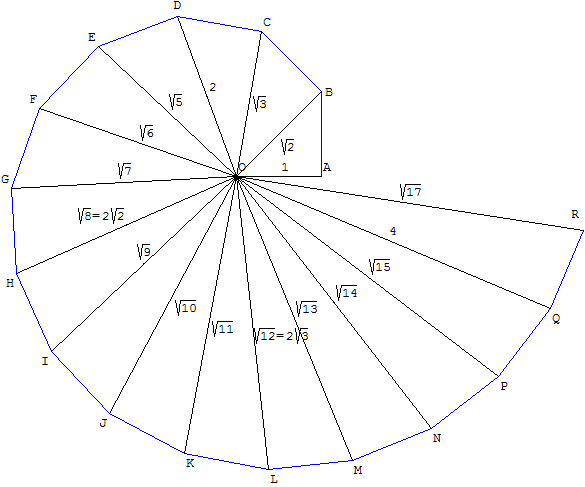
Que Teeteto estableció una teoría más general de los irracionales, según la cual las raíces cuadradas de números no cuadrados son irracionales, se sugiere en el diálogo platónico del mismo nombre, así como en el comentario y los escolios de los Elementos..