Superficie reglada

En geometría, una superficie S es gobernado (también llamado a Pergamino) si a través de cada punto S hay una línea recta que se encuentra en S. Ejemplos incluyen el plano, la superficie lateral de un cilindro o cono, una superficie cónica con directrix elíptico, el conoide derecho, el helicoide y el tangente desarrollado de una curva lisa en el espacio.

Una superficie reglada puede describirse como el conjunto de puntos barridos por una línea recta en movimiento. Por ejemplo, un cono se forma manteniendo fijo un punto de una línea mientras se mueve otro punto a lo largo de un círculo. Una superficie está doblemente reglada si por cada uno de sus puntos pasan dos rectas distintas que recorren la superficie. El paraboloide hiperbólico y el hiperboloide de una hoja son superficies doblemente regladas. El plano es la única superficie que contiene al menos tres líneas distintas que pasan por cada uno de sus puntos (Fuchs y Tabachnikov 2007).

Las propiedades de ser regido o doblemente regido se conservan en los mapas proyectivos y, por lo tanto, son conceptos de geometría proyectiva. En geometría algebraica, las superficies regladas a veces se consideran superficies en un espacio afín o proyectivo sobre un campo, pero también a veces se consideran superficies algebraicas abstractas sin incrustación en un espacio afín o proyectivo, en cuyo caso "línea recta" 34; Se entiende por línea afín o proyectiva.

Definición y representación paramétrica

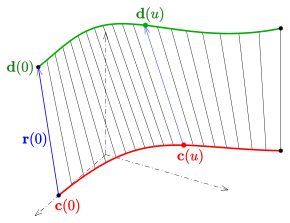
Una variedad diferenciable bidimensional se llama superficie reglada si es la unión de una familia paramétrica de líneas. Las líneas de esta familia son las generadoras de la superficie reglada.

Una superficie reglada se puede describir mediante una representación paramétrica de la forma

• (CR) x()u,v)=c()u)+vr()u) , v▪ ▪ R ,{displaystyle quad mathbf {x} (u,v)={color {red}mathbf {c} (u)}+v;{color {blue}mathbf {r} (u)}\ vin mathbb {R} ~.

Cualquier curva v↦ ↦ x()u0,v){displaystyle ;vmapsto mathbf {x} (u_{0},v);} con parámetro fijo u=u0{displaystyle U=u_{0} es un generador (línea) y la curva u↦ ↦ c()u){displaystyle ;umapsto mathbf {c} (u);} es directrix de la representación. Los vectores r()u)ل ل 0{displaystyle ;mathbf {r} (u)neq {bf {0}} describir las direcciones de los generadores.

La directriz puede colapsar hasta un punto (en el caso de un cono, consulte el ejemplo a continuación).

Alternativamente, la superficie reglada (CR) puede describirse mediante

• (CD) x()u,v)=()1− − v)c()u)+vd()u) {displaystyle quad mathbf {x} (u,v)=(1-v);{color {red}mathbf {c} (u)}+v;{color {grien}mathbf {d} (u)} }

con el segundo directo d()u)=c()u)+r()u){displaystyle ;mathbf {d} (u)=mathbf {c} (u)+mathbf {r} (u);}.

Alternativamente, se puede comenzar con dos curvas no intersectorias c()u),d()u){displaystyle mathbf {c} (u),mathbf {d} (u)} como directrices, y conseguir (CD) una superficie gobernada con direcciones de línea r()u)=d()u)− − c()u) .{displaystyle ;mathbf {r} (u)=mathbf {d} (u)-mathbf {c} (u).}

Para la generación de una superficie gobernada por dos directrices (o una directrix y los vectores de direcciones de línea) no sólo la forma geométrica de estas curvas son esenciales, sino también las representaciones paramétricas especiales de ellas influyen en la forma de la superficie gobernada (ver ejemplos a), d)).

Para la representación de investigaciones teóricas (CR) es más ventajoso, porque el parámetro v{displaystyle v} aparece sólo una vez.

Ejemplos

Cilindro circular derecho

x2+Sí.2=a2 {displaystyle #:

x()u,v)=()a#⁡ ⁡ u,apecado⁡ ⁡ u,v)T{displaystyle mathbf {x} (u,v)=(acos u,asin u,v)^{T}

=()a#⁡ ⁡ u,apecado⁡ ⁡ u,0)T+v()0,0,1)T{displaystyle ={color {red}(acos u,asin u,0)};+;v;{color {blue}(0,0,1)}{T}}

=()1− − v)()a#⁡ ⁡ u,apecado⁡ ⁡ u,0)T+v()a#⁡ ⁡ u,apecado⁡ ⁡ u,1)T .{displaystyle =(1-v);{color {red}(acos u,asin u,0)};+;v;{color {grien}(acos u,asin u,1)}

con

c()u)=()a#⁡ ⁡ u,apecado⁡ ⁡ u,0)T , r()u)=()0,0,1)T , d()u)=()a#⁡ ⁡ u,apecado⁡ ⁡ u,1)T .{displaystyle mathbf {c} (u)=(acos u,asin u,0)^{T}\\mathbf {r} (u)=(0,0,1)^{T}\mathbf {d} (u)=(acos u,asin u,1)^{T}

Cono circular recto

x2+Sí.2=z2 {displaystyle #:

x()u,v)=()#⁡ ⁡ u,pecado⁡ ⁡ u,1)T+v()#⁡ ⁡ u,pecado⁡ ⁡ u,1)T{displaystyle mathbf {x} (u,v)=(cos u,sin u,1)^{T};+;v;(cos u,sin u,1)}

=()1− − v)()#⁡ ⁡ u,pecado⁡ ⁡ u,1)T+v()2#⁡ ⁡ u,2pecado⁡ ⁡ u,2)T.{displaystyle =(1-v);(cos u,sin u,1)};+;v;(2cos u,2sin u,2)^{T}

con c()u)=()#⁡ ⁡ u,pecado⁡ ⁡ u,1)T=r()u) ,d()u)=()2#⁡ ⁡ u,2pecado⁡ ⁡ u,2)T .{displaystyle quad mathbf {c} (u)=(cos u,sin u,1)^{T};=;mathbf {r} (u)quad mathbf {d} (u)=(2cos u,2sin u,2)^{T}).
En este caso uno podría haber usado el ápice como el directrix, es decir: c()u)=()0,0,0)T {fnMicrosoft Sans Serif} y r()u)=()#⁡ ⁡ u,pecado⁡ ⁡ u,1)T {displaystyle mathbf {r} (u)=(cos u,sin u,1)^{T} } como las direcciones de línea.

Para cualquier cono se puede elegir el vértice como directriz. Este caso muestra: La directriz de una superficie reglada puede degenerar en un punto.

Helicoidal

x()u,v)=()v#⁡ ⁡ u,vpecado⁡ ⁡ u,ku)T{displaystyle mathbf {x} (u,v)=;(vcos u,vsin u,ku)^{T};}

=()0,0,ku)T+v()#⁡ ⁡ u,pecado⁡ ⁡ u,0)T {displaystyle =;(0,0,ku)};+;v;(cos u,sin u,0)^{T} }

=()1− − v)()0,0,ku)T+v()#⁡ ⁡ u,pecado⁡ ⁡ u,ku)T .{displaystyle =;(1-v);(0,0,ku)};+;v;(cos u,sin u,ku)^{T}.}

El directrix c()u)=()0,0,ku)T{displaystyle mathbf {c} (u)=(0,0,ku)^{T};} es el eje z, las direcciones de línea son r()u)= ()#⁡ ⁡ u,pecado⁡ ⁡ u,0)T{displaystyle ;mathbf {r} (u)=cos u,sin u,0)^{T};} y el segundo directrix d()u)=()#⁡ ⁡ u,pecado⁡ ⁡ u,ku)T {displaystyle mathbf {d} (u)=(cos u,sin u,ku)^{T} } es un helix.

El helicoide es un caso especial de los helicoides generalizados gobernados.

Cilindro, cono e hiperboloides

La representación paramétrica

x()u,v)=()1− − v)()#⁡ ⁡ ()u− − φ φ ),pecado⁡ ⁡ ()u− − φ φ ),− − 1)T+v()#⁡ ⁡ ()u+φ φ ),pecado⁡ ⁡ ()u+φ φ ),1)T{displaystyle mathbf {x} (u,v)=(1-v);(cos(u-varphi),sin(u-varphi),-1)^{T};+;v;(cos(u+varphi),sin(u+varphi),1)^{T}}}

tiene dos círculos horizontales como directrices. El parámetro adicional φ φ {displaystyle varphi } permite variar las representaciones paramétricas de los círculos. Para

φ φ =0 {displaystyle varphi =0} uno consigue el cilindro x2+Sí.2=1{displaystyle x^{2}+y^{2}=1}Para

φ φ =π π /2 {displaystyle varphi =pi /2} uno consigue el cono x2+Sí.2=z2{displaystyle ¿Qué? y para

<math alttext="{displaystyle 0<varphi 0c)φ φ c)π π /2 {displaystyle 0 madevarphi<img alt="{displaystyle 0<varphi uno consigue un hiperboloide de una hoja con ecuación x2+Sí.2a2− − z2c2=1 {displaystyle {tfrac {x^{2}+y^{2}{a^{2}}-{tfrac} {c} {c}}=1 } y los semi ejes a=#⁡ ⁡ φ φ ,c=cot⁡ ⁡ φ φ {displaystyle a=cos varphi ;,;c=cot varphi }.

Un hiperboloide de una hoja es un doblemente superficie gobernada.

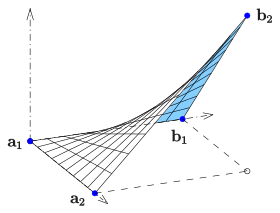
Paraboloide hiperbólico

Si las dos directrices en (CD) son las líneas

c()u)=()1− − u)a1+ua2,d()u)=()1− − u)b1+ub2{displaystyle mathbf {c} (u)=(1-u)mathbf {a} _{1}+umathbf {a} _{2},quad mathbf {d} (u)=(1-u)mathbf {b} _{1}+umathbf {b} ¿Qué?

uno obtiene

x()u,v)=()1− − v)()()1− − u)a1+ua2) + v()()1− − u)b1+ub2) {fnMitbf {x} (u,v)=(1-v){big (}(1-u)mathbf {a} _{1}+umathbf {a} _{2}{2}big)} + v{big (}(1-u)mathbf {b} {}{1} {b}} {b}}}}}b} {b}b} {b}b}}b}}}b}b}}b}b}b}b} {b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b}b},

que es el paraboloide hiperbólico que interpola los 4 puntos a1,a2,b1,b2 {displaystyle mathbf {a} _{1},;mathbf {a} ¿Qué? ¿Qué? ¿Qué? bilinealmente.

Obviamente la superficie reinada es una doble superficie, porque cualquier punto se encuentra en dos líneas de la superficie.

Para el ejemplo que se muestra en el diagrama:

a1=()0,0,0)T,a2=()1,0,0)T,b1=()0,1,0)T,b2=()1,1,1)T {,0};;;;cH9}; {c}cH0}\cH0}=(1,0,0)};;mtbf {b}=(0,0)}= {cH0} {cH0} {c} {c}cH0} {c}} {c}c}c}c}c}c}c}c}cc}cc}c}c}c}c}cccc}ccc}ccc}c}c}c}c}ccccc}cccc}ccc}cccccc}cccc}c}cc}c}cc}c}cccc}c}.

El paraboloide hiperbólico tiene la ecuación z=xSí.{displaystyle z=xy}.

La tira de Möbius

La superficie reglada

x()u,v)=c()u)+vr()u){displaystyle mathbf {x} (u,v)=mathbf {c} (u)+v;mathbf {r} (u)}

con

c()u)=()#⁡ ⁡ 2u,pecado⁡ ⁡ 2u,0)T {displaystyle mathbf {c} (u)=(cos 2u,sin 2u,0)^{T} } (circle as directrix),

<math alttext="{displaystyle mathbf {r} (u)=(cos ucos 2u,cos usin 2u,sin u)^{T}\quad 0leq ur()u)=()#⁡ ⁡ u#⁡ ⁡ 2u,#⁡ ⁡ upecado⁡ ⁡ 2u,pecado⁡ ⁡ u)T ,0≤ ≤ uc)π π ,{displaystyle mathbf {r} (u)=(cos ucos 2u,cos usin 2u,sin u)^{T}quad 0leq u madepi }<img alt="{displaystyle mathbf {r} (u)=(cos ucos 2u,cos usin 2u,sin u)^{T}\quad 0leq u

contiene una tira de Möbius.

El diagrama muestra la tira Möbius para − − 0.3≤ ≤ v≤ ≤ 0.3{displaystyle -0.3leq vleq 0.3}.

Un cálculo simple muestra Det()cÍ Í ()0),rÍ Í ()0),r()0))ل ل 0 {displaystyle det(mathbf {c} (0);;;;mathbf { dot {}} (0);;;mathbf {r} (0));neq;0 } (véase la sección siguiente). De ahí la realización dada de una tira Möbius es no susceptible de desarrollo. Pero existen tiras Möbius de desarrollo.

Más ejemplos

• Conoid
• Superficie catalana
• Rollos de desarrollo (oloide, esphericon)

Planos tangenciales, superficies desarrollables

Para las consideraciones siguientes se supone que existe cualquier derivada necesaria.

Para la determinación del vector normal en un punto uno necesita los derivados parciales de la representación x()u,v)=c()u)+vr()u){displaystyle quad mathbf {x} (u,v)=mathbf {c} (u)+v;mathbf {r} (u)}:

xu=cÍ Í ()u)+vrÍ Í ()u) {displaystyle mathbf {x} _{u}=mathbf { dot {c} (u)+v;mathbf { dot {} (u) }xv=r()u){displaystyle quad mathbf {x} _{v}=;mathbf {r} (u)}

Por lo tanto, el vector normal es

• n=xu× × xv=cÍ Í × × r+v()rÍ Í × × r) .{displaystyle mathbf {n} = 'mathbf {x} ####times mathbf {x} ¿Qué? times mathbf {r} +v(mathbf {dot {r} times mathbf {r}.}

Debido a n⋅ ⋅ r=0{displaystyle mathbf {n} cdot mathbf {r} =0} (Un producto mixto con dos vectores iguales es siempre 0 !), vector r()u0){displaystyle mathbf {r} (u_{0})} es un vector tangente en cualquier punto x()u0,v){displaystyle mathbf {x} (u_{0},v)}. Los planos tangentes a lo largo de esta línea son todos iguales, si rÍ Í × × r{displaystyle mathbf { dot {r} times mathbf {r} es un múltiple de cÍ Í × × r{displaystyle mathbf {dot {c} times mathbf {r}. Esto es posible sólo, si los tres vectores cÍ Í ,rÍ Í ,r {displaystyle mathbf {dot {c} ¿Qué? ;,;mathbf {r} } mienten en un avión, es decir, dependen linealmente. La dependencia lineal de tres vectores se puede comprobar utilizando el determinante de estos vectores:

• Los planos tangentes de la línea x()u0,v)=c()u0)+vr()u0){displaystyle mathbf {x} (u_{0},v)=mathbf {c} (u_{0})+v;mathbf {r} (u_{0})} son iguales, si

Det()cÍ Í ()u0),rÍ Í ()u0),r()u0))=0 .{displaystyle det(mathbf {dot {c} (u_{0});,;;mathbf { dot {r}}} (u_{0});,;;mathbf {r});=;0.}

La importancia de esta condición determinante se muestra en la siguiente afirmación:

• Una superficie gobernada x()u,v)=c()u)+vr()u){displaystyle quad mathbf {x} (u,v)=mathbf {c} (u)+v;mathbf {r} (u)} es desarrollo en un avión, si por cada punto la curvatura Gauss desaparece. Este es exactamente el caso si

Det()cÍ Í ,rÍ Í ,r)=0{displaystyle det(mathbf {dot {c} ¿Qué? ;,;mathbf {r});=;0quad }

en cada punto es verdad.

Los generadores de cualquier superficie reglada se fusionan con una familia de sus líneas asintóticas. Para superficies desarrollables también forman una familia de sus líneas de curvatura. Se puede demostrar que cualquier superficie desarrollable es un cono, un cilindro o una superficie formada por todas las tangentes de una curva espacial.

Aplicación e historia de las superficies urbanizables

La condición determinante para superficies desarrollables se utiliza para determinar conexiones numéricamente desarrollables entre curvas espaciales (directrices). El diagrama muestra una conexión desarrollable entre dos elipses contenidas en diferentes planos (una horizontal, la otra vertical) y su desarrollo.

En Diseño interactivo de superficies desarrollables se ofrece una impresión del uso de superficies desarrollables en el Diseño asistido por ordenador (CAD).

Puede encontrar un estudio histórico sobre superficies desarrollables en Superficies desarrollables: su historia y aplicación.

Superficies regladas en geometría algebraica

En geometría algebraica, las superficies regladas se definieron originalmente como superficies proyectivas en un espacio proyectivo que contenía una línea recta que pasaba por cualquier punto dado. Esto implica inmediatamente que hay una línea proyectiva en la superficie que pasa por cualquier punto dado, y esta condición ahora se usa a menudo como la definición de una superficie reglada: las superficies regladas se definen como superficies proyectivas abstractas que satisfacen esta condición de que hay una línea proyectiva. por cualquier punto. Esto equivale a decir que son birracionales al producto de una curva y una recta proyectiva. A veces se define una superficie reglada como aquella que satisface la condición más fuerte de que tiene una fibración sobre una curva con fibras que son líneas proyectivas. Esto excluye el plano proyectivo, que tiene una línea proyectiva en cada punto pero no puede escribirse como tal fibración.

Las superficies dominadas aparecen en la clasificación de Enriques de superficies complejas proyectivas, porque cada superficie algebraica de la dimensión Kodaira − − JUEGO JUEGO {displaystyle -infty es una superficie gobernada (o un plano proyectivo, si se utiliza la definición restrictiva de la superficie gobernada). Cada superficie proyectada mínima que no sea el plano proyectivo es el paquete proyectivo de un paquete vectorial de 2 dimensiones sobre una curva. Las superficies gobernadas con curva base del género 0 son las superficies Hirzebruch.

Superficies regladas en arquitectura

Las superficies doblemente regladas son la inspiración para estructuras hiperboloides curvas que se pueden construir con una red de elementos rectos, a saber:

• Paraboloides hiperbólicos, como techos de sillas.
• Hiperboloides de una hoja, tales como torres de refrigeración y algunos contenedores de basura.

El motor de cohete RM-81 Agena empleaba canales de enfriamiento rectos que se disponían en una superficie reglada para formar la garganta de la sección de la boquilla.

• 
  Torres hiperbólicas enfriantes en Didcot Power Station, Reino Unido; la superficie se puede gobernar doblemente.
• 
  Doubly gobernó torre de agua con tanque toroidal, por Jan Bogusławski en Ciechanów, Polonia
• 
  Un hiperboloide Kobe Port Tower, Kobe, Japón, con un doble fallo.
• 
  Torre de agua hiperboloide, 1896 en Nizhny Novgorod.
• 
  La cuadrícula de la torre de Shujov en Moscú, cuyas secciones están doblemente gobernadas.
• 
  Una escalera helicoidea gobernada en espiral dentro del Torrazzo de Cremona.
• 
  Iglesia de pueblo en Selo, Eslovenia: tanto el techo (conical) como la pared (cilíndrica) son superficies gobernadas.
• 
  Un techo paraboloide hiperbólico de la estación de tren Warszawa Ochota en Varsovia, Polonia.
• 
  Un sombrero cónico gobernado.
• 
  Azulejos corrugados de techo gobernados por líneas paralelas en una dirección, y sinusoidal en la dirección perpendicular
• 
  Construcción de una superficie planar por decisión (creación) concreta