Sistema cristalino triclínico

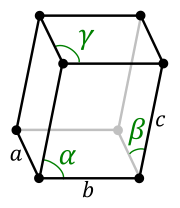
En cristalografía, el sistema cristalino triclínico (o anórtico) es uno de los 7 sistemas cristalinos. Un sistema cristalino se describe mediante tres vectores básicos. En el sistema triclínico, el cristal está descrito por vectores de longitud desigual, como en el sistema ortorrómbico. Además, los ángulos entre estos vectores deben ser todos diferentes y no pueden incluir 90°.
La red triclínica es la menos simétrica de las 14 redes tridimensionales de Bravais. Tiene (en sí mismo) la simetría mínima que tienen todas las redes: puntos de inversión en cada punto de la red y en 7 puntos más para cada punto de la red: en los puntos medios de las aristas y las caras, y en los puntos centrales. Es el único tipo de celosía que no tiene planos de espejo.
Clases de cristal
En la siguiente tabla se enumeran los nombres de clase del sistema cristalino triclínico, ejemplos, notación de Schönflies, notación de Hermann-Mauguin, grupos de puntos, tablas internacionales para cristalografía, número de grupo espacial, orbifold, tipo y grupos espaciales. Hay un total de 2 grupos espaciales.
| # | Grupo de puntos | Tipo | Ejemplo | Grupo espacial | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre | Schönflies | Intl | orbifold | Coxeter | |||||||||||
| 1 | Pedal | C1 | 1 | 11 | [ ]+ | polar enantiomorfo | Tantite | P1 | |||||||
| 2 | Pinacoidal | Ci (S2) | 1 | 1× | [2]+2+] | centros simétricos | Wollastonite | P1 | |||||||
A cada uno solo se le asocia un grupo espacial. Pinacoidal también se conoce como triclínica normal. Pedial es también hemiédrico triclínico.
Los ejemplos minerales incluyen plagioclasa, microclina, rodonita, turquesa, wollastonita y ambligonita, todos en triclínico normal (1).
Contenido relacionado
Ley de Fick
Miscibilidad
Masa molar
Ley de las proporciones múltiples
Anilina