Silla de mono

En matemáticas, la silla de mono es la superficie definida por la ecuación

${displaystyle z=x^{3}-3xy^{2},, }$

o en coordenadas cilíndricas

${displaystyle z=rho ^{3}cos(3varphi). }$

Pertenece a la clase de superficies de sillas, y su nombre deriva de la observación de que una silla para un mono requeriría dos depresiones para las piernas y una para la cola. El punto ${displaystyle (0,0,0)}$ en la silla de mono corresponde a un punto crítico degenerado de la función ${displaystyle z(x,y)}$ a ${displaystyle (0,0)}$. La silla de mono tiene un punto umbilical aislado con curvatura Gausiana cero en el origen, mientras que la curvatura es estrictamente negativa en todos los otros puntos.

Uno puede relacionar las ecuaciones rectangulares y cilíndricas utilizando números complejos ${displaystyle x+iy=re^{ivarphi$

${displaystyle z=x^{3}-3xy^{2}=operatorname {Re} [(x+iy)^{3}]=operatorname {Re} [r^{3}e^{3ivarphi]=r^{3}cos(3varphi).}$

Al reemplazar 3 en la ecuación cilíndrica con cualquier entero ${displaystyle kgeq 1,}$ uno puede crear una silla con ${displaystyle k}$ depresiones.

Otra orientación de la silla de mono es la Pétalo de fundición definidas por ${displaystyle x+y+z+xyz=0,}$ así que z-eje de la silla de mono corresponde a la dirección ${displaystyle (1,1,1)}$ en el pétalo Smelt.

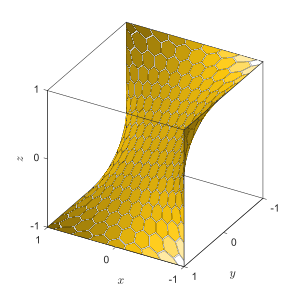
Silla de caballo

El término silla de caballo puede usarse en contraste con silla de mono, para designar una superficie de silla ordinaria en la que z(x,< i>y) tiene un punto de silla, un mínimo o máximo local en cada dirección del plano xy. Por el contrario, la silla de montar tiene un punto de inflexión estacionario en todas direcciones.