Serie armónica (matemáticas)

Compartir Imprimir Citar

Divergente suma de todas las fracciones positivas de las unidades

En matemáticas, la serie armónica es la serie infinita formada al sumar todas las fracciones unitarias positivas:

{displaystyle sum _{n=1}^{infty }{frac {1}{n}}=1+{frac {1}{2}}+{frac {1}{3}}+{frac {1}{4}}+{frac {1}{5}}+cdots.}

La primera $n$ términos de la serie suma a aproximadamente ${displaystyle ln n+gamma }$ , donde $ln$ es el logaritmo natural y ${displaystyle gamma approx 0.577}$ es la constante Euler-Mascheroni. Debido a que el logaritmo tiene valores arbitrariamente grandes, la serie armónica no tiene un límite finito: es una serie divergente. Su divergencia fue probada en el siglo XIV por Nicole Oresme usando un precursor de la prueba de condensación de Cauchy para la convergencia de series infinitas. También se puede probar que se diverjan comparando la suma con una integral, según la prueba integral de convergencia.

Las aplicaciones de la serie armónica y sus sumas parciales incluyen la prueba de Euler de que hay infinitos números primos, el análisis del problema del coleccionista de cupones sobre cuántos ensayos aleatorios se necesitan para proporcionar un rango completo de respuestas, los componentes conectados de gráficos aleatorios, el problema de apilamiento de bloques sobre qué tan lejos del borde de una tabla se puede colocar una pila de bloques en voladizo y el análisis de casos promedio del algoritmo de clasificación rápida.

Historia

Una ola y sus armónicos, con longitudes de onda

{displaystyle 1,{tfrac {1}{2}},{tfrac {1}{3}},dots }

El nombre de la serie armónica deriva del concepto de matices o armónicos en la música: las longitudes de onda de los matices de una cuerda vibradora son ${tfrac {1}{2}}$ , ${tfrac {1}{3}}$ , ${tfrac {1}{4}}$ , etc., de la longitud de onda fundamental de la cuerda. Cada término de la serie armónica después de la primera es el medio armónico de los términos vecinos, por lo que los términos forman una progresión armónica; las frases armónico y progreso armónico También derivan de la música. Más allá de la música, las secuencias armónicas también han tenido cierta popularidad con los arquitectos. Esto fue particularmente en el período barroco, cuando los arquitectos los utilizaron para establecer las proporciones de los planos del piso, de las elevaciones, y para establecer relaciones armónicas entre los detalles arquitectónicos interiores y exteriores de las iglesias y palacios.

La divergencia de la serie armónica fue probada por primera vez en 1350 por Nicole Oresme. El trabajo de Oresme y el trabajo contemporáneo de Richard Swineshead en una serie diferente marcaron la primera aparición de series infinitas distintas de las series geométricas en matemáticas. Sin embargo, este logro cayó en la oscuridad. Pietro Mengoli y Jacob Bernoulli publicaron pruebas adicionales en el siglo XVII. Bernoulli le dio crédito a su hermano Johann Bernoulli por encontrar la prueba, y luego se incluyó en las obras completas de Johann Bernoulli.

Las sumas parciales de la serie armónica fueron llamadas números armónicos, y dada su notación habitual $H_{n}$ , en 1968 por Donald Knuth.

Definición y divergencia

La serie armónica es la serie infinita

{displaystyle sum _{n=1}^{infty }{frac {1}{n}}=1+{frac {1}{2}}+{frac {1}{3}}+{frac {1}{4}}+{frac {1}{5}}+cdots }

Prueba de comparación

Una forma de probar la divergencia es comparar la serie armónica con otra serie divergente, donde cada denominador se reemplaza con la siguiente potencia de dos más grande:

{displaystyle {begin{alignedat}{8}1&+{frac {1}{2}}&&+{frac {1}{3}}&&+{frac {1}{4}}&&+{frac {1}{5}}&&+{frac {1}{6}}&&+{frac {1}{7}}&&+{frac {1}{8}}&&+{frac {1}{9}}&&+cdots \[5pt]{}geq 1&+{frac {1}{2}}&&+{frac {1}{color {red}{mathbf {4} }}}&&+{frac {1}{4}}&&+{frac {1}{color {red}{mathbf {8} }}}&&+{frac {1}{color {red}{mathbf {8} }}}&&+{frac {1}{color {red}{mathbf {8} }}}&&+{frac {1}{8}}&&+{frac {1}{color {red}{mathbf {16} }}}&&+cdots \[5pt]end{alignedat}}}

{displaystyle {begin{aligned}&1+left({frac {1}{2}}right)+left({frac {1}{4}}+{frac {1}{4}}right)+left({frac {1}{8}}+{frac {1}{8}}+{frac {1}{8}}+{frac {1}{8}}right)+left({frac {1}{16}}+cdots +{frac {1}{16}}right)+cdots \[5pt]{}={}&1+{frac {1}{2}}+{frac {1}{2}}+{frac {1}{2}}+{frac {1}{2}}+cdots.end{aligned}}}

entero

k

{displaystyle sum _{n=1}^{2^{k}}{frac {1}{n}}geq 1+{frac {k}{2}}}

prueba integral

Rectángulos con área dada por la serie armónica, y la hiperbola

y=1/x

a través de las esquinas superiores izquierdas de estos rectángulos

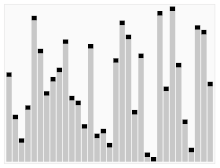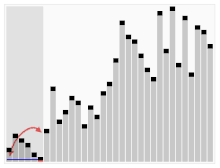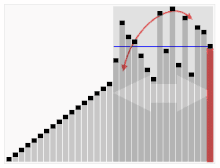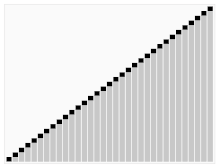
Es posible probar que la serie armónica se divierte comparando su suma con una integral inadecuada. Específicamente, considere la disposición de los rectángulos mostrados en la figura a la derecha. Cada rectángulo es 1 unidad de ancho y ${tfrac 1n}$ unidades altas, así que si la serie armónica converge entonces el área total de los rectángulos sería la suma de la serie armónica. La curva ${displaystyle y={tfrac {1}{x}}}$ permanece completamente por debajo del límite superior de los rectángulos, por lo que el área bajo la curva (en el rango de $x$ de uno a infinito que está cubierto por rectángulos) sería menos que el área de la unión de los rectángulos. Sin embargo, el área debajo de la curva es dada por una intrínseca divergente,

{displaystyle int _{1}^{infty }{frac {1}{x}},dx=infty.}

Reemplazar cada rectángulo por el siguiente en la secuencia produciría una secuencia de rectángulos cuyo límite se encuentra debajo de la curva en lugar de por encima de ella. Esto muestra que las sumas parciales de la serie armónica difieren de la integral por una cantidad que está limitada por encima y por debajo por el área de la unidad del primer rectángulo:

<math alttext="{displaystyle int _{1}^{N+1}{frac {1}{x}},dx<sum _{i=1}^{N}{frac {1}{i}}∫ ∫ 1N+11xdx... i=1N1i.∫ ∫ 1N1xdx+1.{displaystyle int - ¿Por qué? ¿Por qué? {1}{i}cantado ¿Por qué?<img alt="{displaystyle int _{1}^{N+1}{frac {1}{x}},dx<sum _{i=1}^{N}{frac {1}{i}}

n

Sumas parciales

$n$	Resumen parcial de la serie armónica, $H_{n}$
$n$	expresada como una fracción		decimal	tamaño relativo
1	1		~1	1
2	3	/2	1,5	1,5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774

Agregar el primero $n$ términos de la serie armónica produce una suma parcial, llamada número armónico y denotado $H_{n}$ :

{displaystyle H_{n}=sum _{k=1}^{n}{frac {1}{k}}.}

Tasa de crecimiento

Estos números crecen muy lentamente, con un crecimiento logarítmico, como se puede ver en la prueba integral. Más precisamente, por la fórmula de Euler-Maclaurin,

{displaystyle H_{n}=ln n+gamma +{frac {1}{2n}}-varepsilon _{n}}

{displaystyle gamma approx 0.5772}

{displaystyle 0leq varepsilon _{n}leq 1/8n^{2}}

n

Divisibilidad

No hay números armónicos son enteros, excepto para ${displaystyle H_{1}=1}$ . Una manera de probarlo $H_{n}$ no es un entero es considerar el poder más alto de dos $2^{k}$ en el rango desde 1 a 1 $n$ . Si $M$ es el múltiplo menos común de los números de 1 a 1 $n$ , entonces $H_{k}$ puede ser reescrita como una suma de fracciones con iguales denominadores

{displaystyle H_{n}=sum _{i=1}^{n}{tfrac {M/i}{M}}}

{displaystyle M/2^{k}}

,(cuando

1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>

)

M

Otra prueba de que los números armónicos no son enteros observa que el denominador de $H_{n}$ debe ser divisible por todos los números primos superiores $n/2$ , y usa el postulado de Bertrand para probar que este conjunto de primos no es vacío. El mismo argumento implica más fuertemente que, excepto por ${displaystyle H_{1}=1}$ , ${displaystyle H_{2}=1.5}$ , y ${displaystyle H_{6}=2.45}$ , ningún número armónico puede tener una representación decimal terminante. Se ha conjeturado que cada número primo divide a los numeradores de sólo un subconjunto finito de los números armónicos, pero esto sigue sin ser probado.

Interpolación

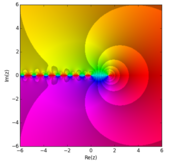
La función digamma en los números complejos

La función digamma se define como la derivada logarítmica de la función gamma

{displaystyle psi (x)={frac {d}{dx}}ln {big (}Gamma (x){big)}={frac {Gamma '(x)}{Gamma (x)}}.}

{displaystyle psi (n)=H_{n-1}-gamma }

aplicaciones

Muchos problemas matemáticos bien conocidos tienen soluciones que involucran la serie armónica y sus sumas parciales.

cruzando un desierto

Solución al problema jeep para

n=3

, mostrando la cantidad de combustible en cada depósito y en el jeep a cada paso

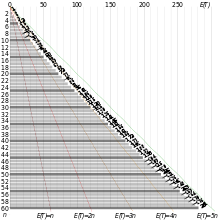
El problema de jeep o el problema del cruce de desierto está incluido en una colección de problemas del siglo IX por Alcuin, Proposiciones ad Acuendos Juvenes (formulado en términos de camellos en lugar de jeeps), pero con una solución incorrecta. El problema pregunta hasta qué punto en el desierto un jeep puede viajar y regresar, a partir de una base con $n$ cargas de combustible, transportando parte del combustible al desierto y dejándolo en depósitos. La solución óptima implica colocar depósitos espaciados a distancias ${displaystyle {tfrac {r}{2n}},{tfrac {r}{2(n-1)}},{tfrac {r}{2(n-2)}},dots }$ desde el punto de partida y el uno al otro, donde $r$ es la distancia que el jeep puede viajar con una sola carga de combustible. En cada viaje hacia fuera y hacia atrás desde la base, el jeep coloca un depósito más, repostando en los otros depósitos a lo largo del camino, y colocando tanto combustible como pueda en el depósito recién colocado mientras todavía deja suficiente para volver a los depósitos anteriores y la base. Por lo tanto, la distancia total alcanzada en $n$ t viaje es

{displaystyle {frac {r}{2n}}+{frac {r}{2(n-1)}}+{frac {r}{2(n-2)}}+cdots ={frac {r}{2}}H_{n},}

H_{n}

n

Por ejemplo, para la versión de Alcuin del problema, ${displaystyle r=30}$ : un camello puede llevar 30 medidas de grano y puede viajar una leuca mientras come una sola medida, donde una leuca es una unidad de distancia aproximadamente igual a 2,3 kilómetros (1,4 mi). El problema tiene $n=3$ : hay 90 medidas de grano, suficiente para abastecer tres viajes. Para la formulación estándar del problema del cruce del desierto, sería posible que el camello viajara ${displaystyle {tfrac {30}{2}}{bigl (}{tfrac {1}{3}}+{tfrac {1}{2}}+{tfrac {1}{1}})=27.5}$ leucas y regreso, colocando un depósito de almacenamiento de granos 5 leucas de la base en el primer viaje y 12.5 leucas de la base en el segundo viaje. Sin embargo, Alcuin en cambio hace una pregunta ligeramente diferente, cuánto grano se puede transportar a una distancia de 30 leucas sin un viaje final de retorno, y ya sea hebras algunos camellos en el desierto o no tiene en cuenta la cantidad de grano consumido por un camello en sus viajes de regreso.

Apilar bloques

El problema de bloqueo: bloques alineados de acuerdo a la serie armónica pueden sobresalir el borde de una tabla por los números armónicos

En el problema de bloqueo, uno debe colocar una pila de $n$ bloques rectangulares idénticos, uno por capa, para que cuelgan lo más lejos posible sobre el borde de una mesa sin caer. El bloque superior se puede colocar con ${tfrac {1}{2}}$ de su longitud que se extiende más allá del siguiente bloque inferior. Si se coloca de esta manera, el siguiente bloque abajo debe ser colocado con ${displaystyle {tfrac {1}{2}}cdot {tfrac {1}{2}}}$ de su longitud que se extiende más allá de la siguiente cuadra inferior, de modo que el centro de masa de los dos primeros bloques es soportado y no se encabezan. El tercer bloque debe ser colocado con la mayoría ${displaystyle {tfrac {1}{2}}cdot {tfrac {1}{3}}}$ de su longitud que se extiende más allá del siguiente bloque inferior, y así sucesivamente. De esta manera, es posible colocar el $n$ bloques de tal manera que se extienden ${displaystyle {tfrac {1}{2}}H_{n}}$ longitudes más allá de la tabla, donde $H_{n}$ es $n$ T número armónico. La divergencia de la serie armónica implica que no hay límite en cuanto más allá de la tabla se puede extender la pila de bloques. Para las pilas con un bloque por capa, no es posible una mejor solución, pero se puede lograr significativamente más overhang usando pilas con más de un bloque por capa.

Contar números primos y divisores

En 1737, Leonhard Euler observó que, como suma formal, la serie armónica es igual a un producto de Euler en el que cada término proviene de un número primo:

{displaystyle sum _{i=1}^{infty }{frac {1}{i}}=prod _{pin mathbb {P} }left(1+{frac {1}{p}}+{frac {1}{p^{2}}}+cdots right)=prod _{pin mathbb {P} }{frac {1}{1-1/p}},}

mathbb {P}

{displaystyle ln prod _{pin mathbb {P} }{frac {1}{1-1/p}}=sum _{pin mathbb {P} }ln {frac {1}{1-1/p}}=sum _{pin mathbb {P} }left({frac {1}{p}}+{frac {1}{2p^{2}}}+{frac {1}{3p^{3}}}+cdots right)=sum _{pin mathbb {P} }{frac {1}{p}}+K.}

K

Otro problema en la teoría de números estrechamente relacionado con la serie armónica se refiere al número promedio de divisores de los números en un rango de 1 a $n$ , formalizado como el orden promedio de la función divisor,

{displaystyle {frac {1}{n}}sum _{i=1}^{n}leftlfloor {frac {n}{i}}rightrfloor leq {frac {1}{n}}sum _{i=1}^{n}{frac {n}{i}}=H_{n}.}

{tfrac 1n}

{displaystyle ln n+2gamma -1+O(1/{sqrt {n}})}

COMECCIÓN COPONES

Gráfico del número de artículos frente al número previsto de juicios necesarios para recoger todos los artículos

Varios juegos o recreaciones comunes implican repetir una selección aleatoria de un conjunto de artículos hasta que se hayan seleccionado todas las opciones posibles; estos incluyen la colección de tarjetas de comercio y la terminación del bingo parkrun, en el que el objetivo es obtener los 60 números posibles de segundos en los tiempos de una secuencia de eventos de ejecución. Las aplicaciones más graves de este problema incluyen el muestreo de todas las variaciones de un producto fabricado para su control de calidad, y la conectividad de gráficos aleatorios. En situaciones de esta forma, una vez que $k$ de un total de $n$ artículos igualmente similares, la probabilidad de recoger un nuevo artículo en una sola elección al azar es $k/n$ y el número esperado de opciones aleatorias necesarias hasta que se recoja un nuevo artículo es $n/k$ . Resumiendo todos los valores de $k$ desde $n$ hasta 1 muestra que el número total esperado de opciones aleatorias necesarias para recoger todos los elementos es ${displaystyle nH_{n}}$ , Donde $H_{n}$ es $n$ T número armónico.

Análisis de algoritmos

Animación de la versión media del surtido rápido, con subproblemas recursivos indicados por flechas sombreadas y con pivotes (elementos rojos y líneas azules) elegidos como el último elemento en cada subproblema

El algoritmo rápido para ordenar un conjunto de elementos se puede analizar utilizando los números armónicos. El algoritmo funciona eligiendo un elemento como "pivot", comparándolo con todos los demás, y clasificando recursivamente los dos subconjuntos de elementos cuya comparación los sitúa antes del pivote y después del pivote. En su complejidad promedio (con la suposición de que todas las permutaciones de entrada son igualmente probables) o en su análisis de tiempo esperado de los insumos de casos peores con una opción aleatoria de pivote, todos los elementos son igualmente probables que sean elegidos como el pivote. Para estos casos, se puede calcular la probabilidad de que dos artículos se comparen uno con otro, a lo largo de la recursión, como función del número de otros elementos que los separan en el orden definitivo. If items $x$ y $y$ están separados $k$ otros elementos, entonces el algoritmo hará una comparación entre $x$ y $y$ sólo cuando, a medida que la recursión progresa, elige $x$ o $y$ como un pivote antes de elegir cualquiera de los otros $k$ artículos entre ellos. Porque cada uno de estos $k+2$ ítems es igualmente probable ser elegido primero, esto sucede con probabilidad ${displaystyle {tfrac {2}{k+2}}}$ . El número total esperado de comparaciones, que controla el tiempo total de funcionamiento del algoritmo, se puede calcular luego resumiendo estas probabilidades sobre todos los pares, dando

{displaystyle sum _{i=2}^{n}sum _{k=0}^{i-2}{frac {2}{k+2}}=sum _{i=1}^{n-1}2H_{i}=O(nlog n).}

Series relacionadas

Serie armónica alterna

Las primeras catorce sumas parciales de la serie armónica alterna (segmentos de líneas negras) muestran convergencia al logaritmo natural de 2 (línea roja).

La serie

{displaystyle sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}=1-{frac {1}{2}}+{frac {1}{3}}-{frac {1}{4}}+{frac {1}{5}}-cdots }

alternando la serie armónica

Explícitamente, la expansión asintótica de la serie es

{displaystyle {frac {1}{1}}-{frac {1}{2}}+cdots +{frac {1}{2n-1}}-{frac {1}{2n}}=H_{2n}-H_{n}=ln 2-{frac {1}{2n}}+O(n^{-2})}

Usar signos alternos con solo fracciones unitarias impares produce una serie relacionada, la fórmula de Leibniz para π

{displaystyle sum _{n=0}^{infty }{frac {(-1)^{n}}{2n+1}}=1-{frac {1}{3}}+{frac {1}{5}}-{frac {1}{7}}+cdots ={frac {pi }{4}}.}

Función zeta de Riemann

La función Riemann zeta se define para real $1}" xmlns="http://www.w3.org/1998/Math/MathML">x■1{displaystyle x confianza1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0549e1fb7ee2023519833093c6e3b60236e7d09f" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>$ por la serie convergente

{displaystyle zeta (x)=sum _{n=1}^{infty }{frac {1}{n^{x}}}={frac {1}{1^{x}}}+{frac {1}{2^{x}}}+{frac {1}{3^{x}}}+cdots}

x=1

excepto

x=1

zeta (2)=pi ^{2}/6

zeta (3)

,parte real

{tfrac {1}{2}}

Serie armónica aleatoria

La serie armónica aleatoria es

{displaystyle sum _{n=1}^{infty }{frac {s_{n}}{n}},}

s_{n}

+1

-1

probabilidad

{tfrac {1}{2}}

.cerca

{tfrac {1}{4}}

-1

1

,que

3

que

-3

.valores

pm 2

{displaystyle {tfrac {1}{8}}-varepsilon }

<math alttext="{displaystyle varepsilon ε ε .10- - 42{displaystyle varepsilon] <img alt="{displaystyle varepsilon

Serie armónica empobrecida

Se puede demostrar que la serie armónica empobrecida en la que se eliminan todos los términos en los que aparece el dígito 9 en cualquier parte del denominador converge al valor 22,92067661926415034816.... De hecho, cuando se eliminan todos los términos que contienen una determinada cadena de dígitos (en cualquier base), la serie converge.

Te puede interesar
Copo de nieve de Koch
(leer más)
Te puede interesar
Función holomorfa
(leer más)
Te puede interesar
Funciones de suelo y techo
(leer más)
Más resultados...