Romboedro

Rhombohedron
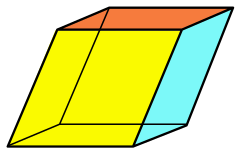Tipo	prisma
Caras	6 rhombi
Edges	12
Vertices	8
Grupo de simetría	Ci+2+], (×), orden 2
Propiedades	convex, equilateral, zonohedron, parallelohedron

En geometría, un romboedro (también llamado hexaedro rómbico o, incorrectamente, romboide) es una figura tridimensional con seis caras que son rombos. Es un caso especial de paralelepípedo donde todos los bordes tienen la misma longitud. Se puede utilizar para definir el sistema reticular romboédrico, un panal con células romboédricas. Un cubo es un caso especial de romboedro con todos sus lados cuadrados.

En general un romboedro puede tener hasta tres tipos de caras rómbicas en pares opuestos congruentes, C_i simetría, orden 2.

Cuatro puntos que forman vértices no adyacentes de un romboedro forman necesariamente los cuatro vértices de un tetraedro ortocéntrico, y todos los tetraedros ortocéntricos pueden formarse de esta manera.

Sistema de celosía romboédrica

El sistema reticular romboédrico tiene células romboédricas, con 6 caras rómbicas congruentes que forman un trapezoedro trigonal:

Casos especiales por simetría

Formulario	Cube	Trigonal trapezohedron	Derecho prisma rhombic	prisma romábico oblicua
Angle limitaciones	α α =β β =γ γ =90∘ ∘ {displaystyle alpha =beta = 'gamma =90^{circ }	α α =β β =γ γ {displaystyle alpha =beta = 'gamma'	α α =β β =90∘ ∘ {displaystyle alpha =beta =90^{circ }	α α =β β {displaystyle alpha =beta }
Simmetría	Oh. Orden 48	D3d Orden 12	D2h Orden 8	C2h Orden 4
Caras	6 plazas	6 rhombi congruente	2 rhombi, 4 plazas	6 rhombi

• Cube: con Oh simetría, orden 48. Todas las caras son cuadrados.
• Trigonal trapezohedron (también llamado isohedral rhombohedron): con D_3d simetría, orden 12. Todos los ángulos internos no obtusos de las caras son iguales (todas las caras son congruentes rhombi). Esto se puede ver estirando un cubo en su eje cuerpo-diagonal. Por ejemplo, un octaedro regular con dos tetrahedra regular pegado en caras opuestas construye un 60 grado trigonal trapezohedron.
• Derecho prisma rhombic: con D_2h simetría, orden 8. Está construido por dos rhombi y cuatro plazas. Esto se puede ver estirando un cubo en su eje diagonal facial. Por ejemplo, dos prismas correctos con bases triangulares regulares unidos hacen un 60 grado prisma rhombic derecho.
• prisma romábico oblicua: con simetría C2h, orden 4. Tiene sólo un plano de simetría, a través de cuatro vértices, y seis caras rhombic.

Geometría sólida

Para una unidad (es decir: con longitud lateral 1) isohedral rhombohedron, con ángulo agudo rhombic Silencio Silencio {displaystyle theta ~, con un vértice en el origen (0, 0, 0), y con un borde acostado a lo largo del eje x, los tres vectores generadores son

e₁: ()1,0,0),{displaystyle {biggl (}1,0,0{biggr)}

e₂: ()#⁡ ⁡ Silencio Silencio ,pecado⁡ ⁡ Silencio Silencio ,0),{displaystyle {biggl (}cos thetasin theta0{biggr)}}

e₃: ()#⁡ ⁡ Silencio Silencio ,#⁡ ⁡ Silencio Silencio − − #2⁡ ⁡ Silencio Silencio pecado⁡ ⁡ Silencio Silencio ,1− − 3#2⁡ ⁡ Silencio Silencio +2#3⁡ ⁡ Silencio Silencio pecado⁡ ⁡ Silencio Silencio ).{displaystyle {biggl (}cos theta{cos theta -cos ^{2}theta over sin theta },{sqrt {1-3cos ^{2}theta +2cos ^{3}theta }}} over sin theta } {biggr)}

Las otras coordenadas se pueden obtener de la suma de los 3 vectores de dirección: e₁ + e₂ e₁ + e₃ e₂ + e₃ y e₁ + e₂ + e₃.

El volumen V{displaystyle V} de un isohedral rhombohedron, en términos de su longitud lateral a{displaystyle a} y su ángulo agudo rhombic Silencio Silencio {displaystyle theta ~, es una simplificación del volumen de un paralelo, y se da por

V=a3()1− − #⁡ ⁡ Silencio Silencio )1+2#⁡ ⁡ Silencio Silencio =a3()1− − #⁡ ⁡ Silencio Silencio )2()1+2#⁡ ⁡ Silencio Silencio )=a31− − 3#2⁡ ⁡ Silencio Silencio +2#3⁡ ⁡ Silencio Silencio .{displaystyle V=a^{3}(1-cos theta){sqrt {1+2cos theta ## {2}(1+2cos theta)}}=a^{3}{3} {sqrt {1-3cos ^{2}theta +2cos ^{3}theta }~

Podemos expresar el volumen V{displaystyle V} otra manera:

V=23 a3pecado2⁡ ⁡ ()Silencio Silencio 2)1− − 43pecado2⁡ ⁡ ()Silencio Silencio 2) .{displaystyle V=2{sqrt {3}~a^{3}sin ^{2}left({frac {theta] - Sí. {1-{frac {4}sin ^{2}left({frac {theta } {2}right)}}}}~}}}}

Como el área de la base (rhombic) es dada por a2pecado⁡ ⁡ Silencio Silencio {displaystyle a^{2}sin theta ~, y como la altura de un romboedro es dada por su volumen dividido por el área de su base, la altura h{displaystyle h} de un isohedral rhombohedron en términos de su longitud lateral a{displaystyle a} y su ángulo agudo rhombic Silencio Silencio {displaystyle theta } es dado por

h=a ()1− − #⁡ ⁡ Silencio Silencio )1+2#⁡ ⁡ Silencio Silencio pecado⁡ ⁡ Silencio Silencio =a 1− − 3#2⁡ ⁡ Silencio Silencio +2#3⁡ ⁡ Silencio Silencio pecado⁡ ⁡ Silencio Silencio .{displaystyle h=a~{(1-cos theta){sqrt {1+2cos theta } over sin theta }=a~{sqrt {1-3cos ^{2}theta +2cos ^{3}theta} over sin theta }~

Nota:

h=a z{displaystyle h=a~z₃ Donde z{displaystyle z}₃ es la tercera coordinación e₃.

La diagonal del cuerpo entre los vértices de ángulos agudos es la más larga. Por simetría rotacional alrededor de esa diagonal, las otras tres diagonales del cuerpo, entre los tres pares de vértices opuestos de ángulos obtusos, tienen todas la misma longitud.