Regula falsa

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método numérico utilizado para soluciones aproximadas de ecuaciones univariadas

En matemáticas, la regula falsi, el método de posición falsa o el método de posición falsa es un método muy antiguo método para resolver una ecuación con una incógnita; este método, en forma modificada, todavía se utiliza. En términos simples, el método es la técnica de prueba y error que consiste en utilizar valores de prueba ("falsos") para la variable y luego ajustar el valor de prueba de acuerdo con el resultado. A esto a veces también se le llama "adivina y comprueba". Las versiones del método son anteriores a la llegada del álgebra y el uso de ecuaciones.

Como ejemplo, considere el problema 26 del papiro Rhind, que pide una solución de (escrita en notación moderna) la ecuación $x + x /4 = 15$ . Esto se soluciona con una posición falsa. Primero, adivina que $x = 4$ para obtener, a la izquierda, 4 + 4/4 = 5. Esta suposición es una buena opción ya que produce un valor entero. Sin embargo, 4 no es la solución de la ecuación original, ya que da un valor tres veces demasiado pequeño. Para compensar, multiplica $x$ (actualmente establecido en 4) por 3 y sustituye nuevamente para obtener 12. + 12/4 = 15, verificando que la solución es $x = 12$ .

Las versiones modernas de la técnica emplean formas sistemáticas de elegir nuevos valores de prueba y se ocupan de la cuestión de si se puede obtener o no una aproximación a una solución y, de ser posible, con qué rapidez se puede encontrar la aproximación.

Dos tipos históricos

Históricamente se pueden distinguir dos tipos básicos de método de posición falsa, posición falsa simple y posición falsa doble.

La Posición falsa simple tiene como objetivo resolver problemas que involucran proporción directa. Estos problemas se pueden escribir algebraicamente en la forma: determine $x$ tal que

{displaystyle ax=b,}

si se conocen $a$ y $b$ . El método comienza utilizando un valor de entrada de prueba $x'$ y encontrando el valor de salida correspondiente $b'$ por multiplicación: $ax' = b'$ . La respuesta correcta se encuentra entonces mediante ajuste proporcional, $x = b / b' x'$ .

Doble posición falsa tiene como objetivo resolver problemas más difíciles que se pueden escribir algebraicamente en la forma: determinar $x$ tal que

{displaystyle f(x)=ax+c=0,}

si se sabe que

{displaystyle f(x_{1})=b_{1},qquad f(x_{2})=b_{2}.}

La doble posición falsa es matemáticamente equivalente a la interpolación lineal. Al utilizar un par de entradas de prueba y el par de salidas correspondiente, el resultado de este algoritmo dado por,

{displaystyle x={frac {b_{1}x_{2}-b_{2}x_{1}}{b_{1}-b_{2}}},}

sería memorizado y realizado de memoria. De hecho, la regla dada por Robert Recorde en su Ground of Artes (c. 1542) es:

Gesse en este woorke como happe doth leade.
Por castigo a la verdad puede proceder.
Y primero temblando por la pregunta,
Aunque no hay verdad en eso sea don.
Tal falsedad es tan buena tierra,
Esa verdad pronto será encontrada.
De muchos bate a muchos mo,
De a pocos tomar a pocos también.
Con mucho ioyne a pocas de nuevo,
A poco añadir a muchas llanuras.
En los crossewaies se multiplican por contrario,
Toda la verdad por falsedades para Fynde.

Para una función lineal afín,

{displaystyle f(x)=ax+c,}

la doble posición falsa proporciona la solución exacta, mientras que para una función no lineal $f$ proporciona una aproximación que puede mejorarse sucesivamente mediante iteración.

Historia

La técnica simple de la posición falsa se encuentra en tablillas cuneiformes de las antiguas matemáticas babilónicas y en papiros de las antiguas matemáticas egipcias.

La doble posición falsa surgió en la antigüedad tardía como un algoritmo puramente aritmético. En el antiguo texto matemático chino llamado Los nueve capítulos sobre el arte matemático (九章算術), que data del 200 a. C. al 100 d. C., la mayor parte del capítulo 7 estaba dedicado al algoritmo. Allí, el procedimiento se justificó con argumentos aritméticos concretos y luego se aplicó creativamente a una amplia variedad de problemas narrativos, incluido uno que involucraba lo que llamaríamos líneas secantes en una sección cónica. Un ejemplo más típico es esta "compra conjunta" problema que implica una situación de "exceso y déficit" condición:

Ahora un artículo se compra conjuntamente; todos contribuyen 8 [coins], el exceso es 3; todos contribuyen 7, el déficit es 4. Dime: El número de personas, el precio del artículo, ¿qué es cada una? Respuesta: 7 personas, precio 53.

Entre los siglos IX y X, el matemático egipcio Abu Kamil escribió un tratado hoy perdido sobre el uso de la doble posición falsa, conocido como el Libro de los Dos Errores (Kitāb al -khaṭāʾayn). El escrito más antiguo que se conserva sobre la doble posición falsa en Oriente Medio es el de Qusta ibn Luqa (siglo X), un matemático árabe de Baalbek, Líbano. Justificó la técnica mediante una prueba geométrica formal de estilo euclidiano. Dentro de la tradición de las matemáticas musulmanas medievales, la doble posición falsa se conocía como hisāb al-khaṭāʾayn ("calcular mediante dos errores"). Se utilizó durante siglos para resolver problemas prácticos como cuestiones comerciales y jurídicas (particiones de bienes según las reglas de la herencia coránica), así como problemas puramente recreativos. El algoritmo a menudo se memorizaba con la ayuda de mnemónicos, como un verso atribuido a Ibn al-Yasamin y diagramas de balanza explicados por al-Hassar e Ibn al-Banna, los tres matemáticos de origen marroquí.

Leonardo de Pisa (Fibonacci) dedicó el capítulo 13 de su libro Liber Abaci (1202 d.C.) a explicar y demostrar los usos de la doble posición falsa, denominando al método regulis elchatayn según el método al-khaṭāʾayn que había aprendido de fuentes árabes. En 1494, Pacioli utilizó el término el cataym en su libro Summa de arithmetica, probablemente tomando el término de Fibonacci. Otros escritores europeos seguirían a Pacioli y en ocasiones proporcionarían una traducción al latín o a la lengua vernácula. Por ejemplo, Tartaglia traduce la versión latinizada del término de Pacioli a la lengua vernácula "falsas posiciones"; en 1556. El término de Pacioli casi desapareció en las obras europeas del siglo XVI y la técnica recibió varios nombres como "Regla de lo falso", "Regla de posición" y "Regla de la posición falsa". Regula Falsi aparece como la versión latinizada de Rule of False ya en 1690.

Varios autores europeos del siglo XVI sintieron la necesidad de pedir disculpas por el nombre del método en una ciencia que busca encontrar la verdad. Por ejemplo, en 1568 Humphrey Baker dice:

La regla de la falsedad no es así por lo que enseña a cualquiera engaño o falsedad, pero que por números falsos tomados en todas las aduenturas, enseña a descubrir el verdadero número que es demagado, y esto de todas las Reglas vulgares que están en práctica) es usted^e la mayor excelencia.

Análisis numérico

El método de posición falsa proporciona una solución exacta para funciones lineales, pero técnicas algebraicas más directas han suplantado su uso para estas funciones. Sin embargo, en el análisis numérico, la doble posición falsa se convirtió en un algoritmo de búsqueda de raíces utilizado en técnicas iterativas de aproximación numérica.

Muchas ecuaciones, incluidas la mayoría de las más complicadas, sólo pueden resolverse mediante una aproximación numérica iterativa. Este consiste en prueba y error, en el que se prueban varios valores de la cantidad desconocida. Ese ensayo y error puede guiarse calculando, en cada paso del procedimiento, una nueva estimación de la solución. Hay muchas maneras de llegar a una estimación calculada y regula falsi proporciona una de ellas.

Dada una ecuación, mueve todos sus términos hacia un lado para que tenga la forma, $f (x) = 0$ , donde $f$ es alguna función de la variable desconocida $x$ . Un valor $c$ que satisface esta ecuación, es decir, $f (c) = 0$ , se llama raíz o cero de la función $f$ y es una solución de la ecuación original. Si $f$ es una función continua y existen dos puntos $a 0$ y $b 0$ tal que $f (a 0)$ y $f (b 0)$ son de signos opuestos, entonces, según el teorema del valor intermedio, la función $f$ tiene una raíz en el intervalo $(a 0, b 0)$ .

Existen muchos algoritmos de búsqueda de raíces que se pueden utilizar para obtener aproximaciones a dicha raíz. Uno de los más comunes es el método de Newton, pero puede no encontrar una raíz en determinadas circunstancias y puede resultar costoso desde el punto de vista computacional, ya que requiere un cálculo de la derivada de la función. Se necesitan otros métodos y una clase general de métodos son los métodos de paréntesis de dos puntos. Estos métodos proceden produciendo una secuencia de intervalos de reducción $[a k, b k]$ , en el $k$ ésimo paso , de modo que $(a k, b k)$ contiene una raíz de $f$ .

Métodos de bracketing de dos puntos

Estos métodos comienzan con dos valores $x$ , encontrados inicialmente mediante prueba y error, en los cuales $f (x)$ tiene signos opuestos. Bajo el supuesto de continuidad, se garantiza que una raíz de $f$ se encuentra entre estos dos valores, es decir, estos valores &# 34;soporte" la raíz. Luego se selecciona un punto estrictamente entre estos dos valores y se utiliza para crear un intervalo más pequeño que todavía encierra una raíz. Si $c$ es el punto seleccionado, entonces el intervalo más pequeño va desde $c$ al punto final donde $f (x)$ tiene el signo opuesto al de $f (c)$ . En el caso improbable de que $f (c) = 0$ , se ha encontrado una raíz y el algoritmo se detiene. De lo contrario, el procedimiento se repite tantas veces como sea necesario para obtener una aproximación a la raíz con la precisión deseada.

El punto seleccionado en cualquier intervalo actual puede considerarse como una estimación de la solución. Las diferentes variaciones de este método implican diferentes formas de calcular esta estimación de solución.

Preservar el bracketing y asegurar que las estimaciones de la solución se encuentren en el interior de los intervalos de bracketing garantiza que las estimaciones de la solución convergerán hacia la solución, una garantía que no está disponible con otros métodos de búsqueda de raíces como el método de Newton o el método secante.

La variación más simple, llamada método de bisección, calcula la estimación de la solución como el punto medio del intervalo entre corchetes. Es decir, si en el paso $k$ , el intervalo de horquillado actual es $[a k, b k]$ , luego el La nueva estimación de la solución $c k$ se obtiene mediante,

{displaystyle c_{k}={frac {a_{k}+b_{k}}{2}}.}

Esto garantiza que $c k$ esté entre $a k$ y $b k$ , garantizando así la convergencia hacia la solución.

Dado que la longitud del intervalo de paréntesis se reduce a la mitad en cada paso, el error del método de bisección se reduce, en promedio, a la mitad con cada iteración. Por lo tanto, cada 3 iteraciones, el método gana aproximadamente un factor de 2³, es decir, aproximadamente un decimal, en precisión.

El método de la regula falsi (posición falsa)

La tasa de convergencia del método de bisección posiblemente podría mejorarse utilizando una estimación de solución diferente.

El método regula falsi calcula la nueva estimación de la solución como la intersección con el eje x del segmento de línea que une los puntos finales de la función en el intervalo de horquillado actual. Esencialmente, la raíz se aproxima reemplazando la función real por un segmento de línea en el intervalo entre corchetes y luego usando la fórmula clásica de doble posición falsa en ese segmento de línea.

Más precisamente, supongamos que en la $k$ -ésima iteración el intervalo entre corchetes es $(a k, b k). Construya la línea que pasa por los puntos (a k, f (a k)) y (b k, f (b k)), como se ilustra. Esta recta es una secante o cuerda de la gráfica de la función f . En forma punto-pendiente, su ecuación viene dada por$

{displaystyle y-f(b_{k})={frac {f(b_{k})-f(a_{k})}{b_{k}-a_{k}}}(x-b_{k}).}

Ahora elija $c k$ para que sea el $x$ -intersección de esta línea, es decir, el valor de $x$ para el cual $y = 0$ , y sustituya estos valores para obtener

{displaystyle f(b_{k})+{frac {f(b_{k})-f(a_{k})}{b_{k}-a_{k}}}(c_{k}-b_{k})=0.}

Resolver esta ecuación para c_k da:

{displaystyle c_{k}=b_{k}-f(b_{k}){frac {b_{k}-a_{k}}{f(b_{k})-f(a_{k})}}={frac {a_{k}f(b_{k})-b_{k}f(a_{k})}{f(b_{k})-f(a_{k})}}.}

Esta última forma simétrica tiene una ventaja computacional:

A medida que se aborda una solución, $a k$ y $b k$ estarán muy juntos y casi siempre serán del mismo signo. En tal resta se pueden perder dígitos significativos. Porque $f (b k)$ y $f (a k)$ son siempre de signo opuesto a la “resta ”en el numerador de la fórmula mejorada es efectivamente una suma (al igual que la resta en el denominador).

En la iteración número $k$ , el número $c k$ se calcula como arriba y luego, si $f (a k)$ y $f (c k a k + 1 = c k y b k + 1 = b k; de lo contrario, establezca un k + 1 = un k y b k + 1 = c k . Este proceso se repite hasta que la raíz se aproxime lo suficiente.$

La fórmula anterior también se usa en el método de la secante, pero el método de la secante siempre retiene los dos últimos puntos calculados y, por lo tanto, aunque es ligeramente más rápido, no conserva el bracketing y es posible que no converja.

El hecho de que regula falsi siempre converge y tiene versiones que funcionan bien para evitar desaceleraciones, lo convierte en una buena opción cuando se necesita velocidad. Sin embargo, su tasa de convergencia puede caer por debajo de la del método de bisección.

Análisis

Desde los puntos finales iniciales $a 0$ y $b 0$ se eligen de manera que $f (a 0)$ y $f (b 0)$ son de signos opuestos, en cada paso, uno de los los puntos finales se acercarán a una raíz de $f$ . Si la segunda derivada de $f$ es de signo constante (por lo que no hay punto de inflexión) en el intervalo, entonces un punto final (aquel donde $f$ también tiene el mismo signo) permanecerá fijo para todos los siguientes iteraciones mientras el punto final convergente se actualiza. Como resultado, a diferencia del método de bisección, el ancho del corchete no tiende a cero (a menos que el cero esté en un punto de inflexión alrededor del cual $signo(f) = -signo(f ")). Como consecuencia, la aproximación lineal a f (x), que se utiliza para elegir la posición falsa, no mejora tan rápidamente como sea posible.$

Un ejemplo de este fenómeno es la función

{displaystyle f(x)=2x^{3}-4x^{2}+3x}

en el soporte inicial [-1,1]. El extremo izquierdo, −1, nunca se reemplaza (no cambia al principio y después de las primeras tres iteraciones, $f "$ es negativo en el intervalo) y por lo tanto el ancho del corchete nunca cae por debajo de 1. Por lo tanto, el punto final derecho se aproxima a 0 en una tasa lineal (el número de dígitos precisos crece linealmente, con una tasa de convergencia de 2/3).

Para funciones discontinuas, solo se puede esperar que este método encuentre un punto donde la función cambia de signo (por ejemplo en $x = 0$ para $1/x$ o la función de signo). Además de los cambios de signo, también es posible que el método converja a un punto donde el límite de la función sea cero, incluso si la función no está definida (o tiene otro valor) en ese punto (por ejemplo en $x = 0$ para la función dada por $f (x) = abs(x) - x 2$ cuando $x \neq 0$ y por $f (0) = 5$ , comenzando con el intervalo [-0.5, 3.0]). Es matemáticamente posible con funciones discontinuas que el método no converja a un límite cero o a un cambio de signo, pero esto no es un problema en la práctica ya que requeriría una secuencia infinita de coincidencias para que ambos puntos finales se atasquen convergiendo en discontinuidades donde el signo no cambia, por ejemplo en $x = \pm1$ en

{displaystyle f(x)={frac {1}{(x-1)^{2}}}+{frac {1}{(x+1)^{2}}}.}

El método de bisección evita este hipotético problema de convergencia.

Mejoras en la regulación falsa

Aunque la regula falsi siempre converge, normalmente considerablemente más rápido que la bisección, hay situaciones que pueden ralentizar su convergencia, a veces hasta un grado prohibitivo. Ese problema no es exclusivo de regula falsi: aparte de la bisección, todos los métodos de resolución de ecuaciones numéricas pueden tener un problema de convergencia lenta o de no convergencia bajo algunas condiciones. A veces, el método de Newton y el método de la secante divergen en lugar de converger, y a menudo lo hacen en las mismas condiciones que frenan la convergencia de la regula falsa.

Pero, aunque regula falsi es uno de los mejores métodos, e incluso en su versión original no mejorada, a menudo sería la mejor opción; por ejemplo, cuando no se utiliza la ecuación de Newton porque la evaluación de la derivada requiere mucho tiempo, o cuando la ecuación de Newton y las sustituciones-sucesivas no han logrado converger.

El modo de

fallo Regula false es fácil de detectar: el mismo punto final se retiene dos veces seguidas. El problema se soluciona fácilmente eligiendo en su lugar una posición falsa modificada, elegida para evitar ralentizaciones debidas a situaciones desfavorables relativamente inusuales. Se han propuesto varias mejoras de este tipo en la regula falsi; dos de ellos, el algoritmo de Illinois y el algoritmo de Anderson-Björk, se describen a continuación.

El algoritmo de Illinois

El algoritmo de Illinois reduce a la mitad el valor $y$ del punto final retenido en el siguiente cálculo de estimación cuando la nueva $y$ -valor (es decir, $f (c k$ )) tiene el mismo signo que el anterior ( $f (c k - 1$ )), lo que significa que se mantendrá el punto final del paso anterior. Por eso:

{displaystyle c_{k}={frac {{frac {1}{2}}f(b_{k})a_{k}-f(a_{k})b_{k}}{{frac {1}{2}}f(b_{k})-f(a_{k})}}}

{displaystyle c_{k}={frac {f(b_{k})a_{k}-{frac {1}{2}}f(a_{k})b_{k}}{f(b_{k})-{frac {1}{2}}f(a_{k})}},}

reducir el peso de uno de los valores del punto final para forzar el siguiente $c k$ que ocurra en ese lado de la función. El factor ½ utilizado anteriormente parece arbitrario, pero garantiza una convergencia superlineal (asintóticamente, el algoritmo realizará dos pasos regulares después de cualquier paso modificado y tiene un orden de convergencia de 1,442). Hay otras formas de elegir el reescalamiento que dan tasas de convergencia superlineal aún mejores.

Algunos estudiosos denominan algoritmo de Illinois al ajuste anterior de la regula falsi. Ford (1995) resume y analiza esta y otras variantes superlineales similares del método de posición falsa.

Algoritmo de Anderson-Björck

Supongamos que en la $k$ -ésima iteración el intervalo de horquillado es $[a k, b k]$ y que el valor funcional de la nueva estimación calculada $c k$ tiene el mismo signo que $f (b k)$ . En este caso, el nuevo intervalo de horquillado $[a k + 1, b k + 1] = [a k, c k]$ y se ha conservado el punto final izquierdo. (Hasta ahora, es lo mismo que la Regula Falsi ordinaria y el algoritmo de Illinois).

Pero, mientras que el algoritmo de Illinois multiplicaría $f (a k)$ por 1/2, el algoritmo de Anderson-Björck lo multiplica por $m$ , donde $m$ tiene uno de los dos valores siguientes:

0,\{frac {1}{2}}&{text{otherwise.}}end{cases}}end{aligned}}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">m.=1− − f()ck)f()bk),m={}m.si m.■0,12de lo contrario.{displaystyle {begin{aligned}m' limit=1-{frac {f(c_{k}{f(b_{k}}}}}\m cl={begin{cases}m'ciendo{text{if} Estoy confundida.0,\{frac {1}{2}}&{text{otherwise.}}end{cases}}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-display mw-invert skin-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/51224305d6a010f2a37e5c526c99b0ff5e1505d3" style="vertical-align: -5.838ex; width:24.341ex; height:12.843ex;"/>

Para raíces simples, Anderson–Björck funciona muy bien en la práctica.

Método ITP

Dado ${displaystyle kappa _{1}in (0,infty),kappa _{2}in left[1,1+phi right)}$ , ${displaystyle n_{1/2}equiv lceil (b_{0}-a_{0})/2epsilon rceil }$ y ${displaystyle n_{0}in [0,infty)}$ Donde ${displaystyle phi }$ es la ración de oro ${displaystyle {tfrac {1}{2}}(1+{sqrt {5}})}$ , en cada iteración ${displaystyle j=0,1,2...}$ el método ITP calcula el punto ${displaystyle x_{text{ITP}}}$ siguientes tres pasos:

[Paso de Interpolación] Calcular la bisección y los puntos de falsi regulador: ${displaystyle x_{1/2}equiv {frac {a+b}{2}}}$ y ${displaystyle x_{f}equiv {frac {bf(a)-af(b)}{f(a)-f(b)}}}$ ;
[Paso de ejecución] Perturbe el estimador hacia el centro: ${displaystyle x_{t}equiv x_{f}+sigma delta }$ Donde ${displaystyle sigma equiv {text{sign}}(x_{1/2}-x_{f})}$ y ${displaystyle delta equiv min{kappa _{1}|b-a|^{kappa _{2}},|x_{1/2}-x_{f}|}}$ ;
[Projection Step] Proyecte el estimador a intervalo minmax: ${displaystyle x_{text{ITP}}equiv x_{1/2}-sigma rho _{k}}$ Donde ${displaystyle rho _{k}equiv min left{epsilon 2^{n_{1/2}+n_{0}-j}-{frac {b-a}{2}},|x_{t}-x_{1/2}|right}}$ .

El valor de la función ${displaystyle f(x_{text{ITP}})}$ en este punto es preguntado, y el intervalo se reduce para entretener la raíz manteniendo el subintervalo con valores de función de signo opuesto en cada extremo. Este procedimiento de tres pasos garantiza que las propiedades minmax del método de bisección son disfrutadas por la estimación así como la convergencia superlineal del método de secant. Y, se observa que se superponen tanto los métodos bisección como los métodos basados en la interpolación bajo funciones lisas y no mojadas.

Consideraciones prácticas

Al resolver una ecuación, o solo algunas, usando una computadora, el método de bisección es una opción adecuada. Aunque la bisección no es tan rápida como los otros métodos (cuando funcionan mejor y no tienen problemas), se garantiza que la bisección convergerá a una velocidad útil, reduciendo aproximadamente a la mitad el error con cada uno. iteración: gana aproximadamente un decimal de precisión con cada 3 iteraciones.

Para el cálculo manual, mediante calculadora, uno tiende a querer utilizar métodos más rápidos y, por lo general, aunque no siempre, convergen más rápido que la bisección. Pero una computadora, incluso usando la bisección, resolverá una ecuación, con la precisión deseada, tan rápidamente que no hay necesidad de intentar ahorrar tiempo usando un método menos confiable, y cada método es menos confiable que la bisección.

Una excepción sería si el programa de computadora tuviera que resolver ecuaciones muchas veces durante su ejecución. Entonces el tiempo ahorrado por los métodos más rápidos podría ser significativo.

Entonces, un programa podría comenzar con el método de Newton y, si el de Newton no converge, cambiar a regula falsi, tal vez en una de sus versiones mejoradas. Versiones, como las versiones Illinois o Anderson-Björck. O, si ni siquiera eso converge tan bien como lo haría la bisección, cambie a la bisección, que siempre converge a un ritmo útil, si no espectacular.

Cuando el cambio en $y$ se ha vuelto muy pequeño y $x$ también está cambiando muy poco, entonces lo más probable es que el método de Newton no tenga problemas y converja. Entonces, bajo esas condiciones favorables, uno podría cambiar al método de Newton si quisiera que el error fuera muy pequeño y quisiera una convergencia muy rápida.

Ejemplo: Crecimiento de una espadaña

En el capítulo 7 de Los Nueve Capítulos, un problema de búsqueda de raíces se puede traducir al lenguaje moderno de la siguiente manera:

Exceso y problema de déficit #11:
Un bulrush creció 3 unidades en su primer día. Al final de cada día, se observa que la planta ha crecido 1/2 del crecimiento del día anterior.
Un club-rush creció 1 unidad en su primer día. Al final de cada día, la planta ha crecido 2 veces más que el crecimiento del día anterior.
Encontrar el tiempo [en días fraccionados] que el pincel del club se hace tan alto como el baluarte.
Respuesta: ${displaystyle (2+{frac {6}{13}})}$ días; la altura es ${displaystyle (4+{frac {8}{10}}+{frac {6}{130}})}$ unidades.
Explicación:
Supongamos que es el día 2. El cepillo del club es más corto que el bulrush por 1,5 unidades.
Supongamos que es el día 3. El cepillo de clubes es más alto que el baluarte por 1,75 unidades. ∎

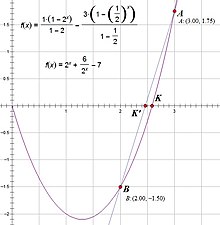
Para entender esto, modelaremos las alturas de las plantas el día $n$ ( $n$ = 1, 2, 3...) después de una serie geométrica.

{displaystyle B(n)=sum _{i=1}^{n}3cdot {frac {1}{2^{i-1}}}quad }

Bulrush

{displaystyle C(n)=sum _{i=1}^{n}1cdot 2^{i-1}quad }

Club-rush

Por el bien de las mejores notaciones, ${displaystyle k=i-1~.}$ Reescribir la serie de altura de la planta ${displaystyle B(n), C(n) }$ en términos de $k$ e invocar la fórmula de la suma.

{displaystyle B(n)=sum _{k=0}^{n-1}3cdot {frac {1}{2^{k}}}=3left({frac {1-({tfrac {1}{2}})^{n-1+1}}{1-{tfrac {1}{2}}}}right)=6left(1-{frac {1}{2^{n}}}right)}

{displaystyle C(n)=sum _{k=0}^{n-1}2^{k}={frac {~~1-2^{n}}{ 1-2 }}=2^{n}-1 }

Ahora, uso regulación falsi encontrar la raíz de ${displaystyle (C(n)-B(n)) }$

{displaystyle F(n):=C(n)-B(n)={frac {6}{2^{n}}}+2^{n}-7 }

Set ${displaystyle x_{1}=2 }$ y computación ${displaystyle F(x_{1})=F(2) }$ que es igual $-1.5$ (el "deficit").
Set ${displaystyle x_{2}=3 }$ y computación ${displaystyle F(x_{2})=F(3) }$ que es igual $1.75$ (el "exceso").

Raíz estimada (primera iteración):

{displaystyle {hat {x}}~=~{frac {~x_{1}F(x_{2})-x_{2}F(x_{1})~}{F(x_{2})-F(x_{1})}}~=~{frac {~2times 1.75+3times 1.5~}{1.75+1.5}}~approx ~2.4615 }

Código de ejemplo

Este programa de ejemplo, escrito en el lenguaje de programación C, es un ejemplo del algoritmo de Illinois. Para encontrar el número positivo $x$ donde $cos(x) = x 3$ , la ecuación se transforma en una forma para encontrar raíces $f (x) = porque(x) -- x 3 = 0$ .

#include Identificado.h#include - No.doble f()doble x) {} Regreso #()x) - x*x*x;}/* a,b: puntos finales de un intervalo donde buscamos e: mitad del límite superior por error relativo m: número máximo de iteración*/doble FalsiMethod()doble ()*f)doble), doble a, doble b, doble e, int m) {} doble c, fc; int n, lado = 0; /* valores de inicio en puntos finales de intervalo */ doble fa = f()a); doble fb = f()b); para ()n = 0; n c) m; n++) {} c = ()fa * b - fb * a) / ()fa - fb); si ()fabs()b - a) c) e * fabs()b + a) descanso; fc = f()c); si ()fc * fb ■ 0) {} /* fc y fb tienen el mismo signo, copia c a b */ b = c; fb = fc; si ()lado == -1) fa /= 2; lado = -1; } más si ()fa * fc ■ 0) {} /* fc y fa tienen el mismo signo, copia c a un */ a = c; fa = fc; si ()lado == +1) fb /= 2; lado = +1; } más {} /* fc * f_ muy pequeño (parece como cero) */ descanso; } } Regreso c;}int principal()vacío) {} printf()# 0.15fn", FalsiMethod()"f, 0, 1, 5E-15, 100)); Regreso 0;}

Después de ejecutar este código, la respuesta final es aproximadamente 0,865474033101614.

Contenido relacionado

Más resultados...