Punto de silla

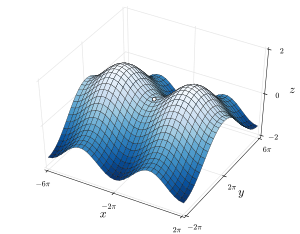
En matemáticas, a punto de entristecimiento o minimax punto es un punto en la superficie del gráfico de una función donde las pendientes (derivativas) en direcciones ortogonales son todos cero (un punto crítico), pero que no es un extremum local de la función. Un ejemplo de un punto de sillín es cuando hay un punto crítico con un mínimo relativo a una dirección axial (entre picos) y en un máximo relativo a lo largo del eje cruzado. Sin embargo, un punto de silla no necesita estar en esta forma. Por ejemplo, la función ${displaystyle f(x,y)=x^{2}+y^{3}$ tiene un punto crítico ${displaystyle (0,0)}$ que es un punto de silla ya que no es ni un mínimo relativo máximo ni relativo, pero no tiene un mínimo relativo máximo o relativo en el ${displaystyle y}$- dirección.

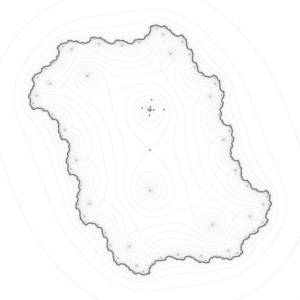
El nombre deriva del hecho de que el ejemplo prototípico en dos dimensiones es una superficie que se curva hacia arriba en una dirección y se curva hacia abajo en una dirección diferente, asemejándose a una Silla de montar o un paso de montaña entre dos picos que forman una silla de montar. En términos de curvas de nivel, un punto de silla en dos dimensiones da lugar a un mapa de curvas de nivel con un par de líneas que se cruzan en el punto. Estas intersecciones son raras en los mapas de estudios de artillería reales, ya que es poco probable que la altura del punto de silla coincida con los múltiplos enteros utilizados en dichos mapas. En cambio, el punto de silla aparece como un espacio en blanco en medio de cuatro conjuntos de líneas de contorno que se acercan y se alejan de él. Para un punto de silla básico, estos conjuntos se presentan en pares, con un par alto opuesto y un par bajo opuesto colocados en direcciones ortogonales. Las curvas de nivel críticas generalmente no tienen que cruzarse ortogonalmente.

Debate matemático

Un simple criterio para comprobar si un determinado punto estacionario de una función de valor real F()x,Sí.) de dos variables reales es un punto de sillín es calcular la matriz hesiana de la función en ese momento: si el hesiano es indefinido, entonces ese punto es un punto de sillín. Por ejemplo, la matriz hesiana de la función ${displaystyle z=x^{2}-y^{2}$ en el punto estacionario ${displaystyle (x,y,z)=(0,0,0)}$ es la matriz

${displaystyle {begin{bmatrix}2 âTMa âTMa âTMa {$