Número de Nusselt

Ajustar Compartir Imprimir Citar

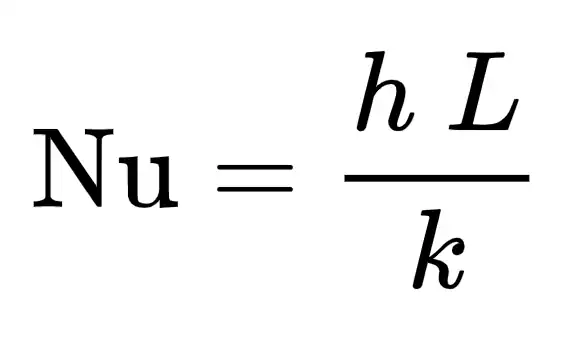
El número de Nusselt (Nu), es la proporción entre la transferencia de calor ocurrida por convección y aquella ocurrida por conducción, que tiene un fluido en una de sus superficies. El número de Nusselt representa que tanto del calor transferido ocurre por convección (movimiento dentro del sistema termodinámico).

Su nombre se debe al ingeniero alemán Wilhelm Nusselt, y es un concepto fundamental en la dinámica de fluidos térmicos. Este número es adimensional, pues no se mide en ningún tipo de unidades, y representa solamente la relación convección/conducción en la frontera de un fluido. Por convección se entiende tanto la advección (movimiento del fluido) como la difusión (conducción interna del fluido).

Su fórmula es Nu = hL / k, donde:

h = coeficiente de transferencia
convectiva
L = longitud característica
k = conductividad térmica

Para obtener este número, se compara heurísticamente una situación ceteris paribus (en iguales circunstancias) de transferencia de calor por convección junto a una situación de transferencia de calor por conducción, pero, en un fluido hipotéticamente inmóvil.

El valor del número de Nusselt proporciona información crucial sobre el tipo de flujo y la eficiencia de la transferencia de calor en el fluido. Un número de Nusselt igual a uno (Nu=1) indica una transferencia de calor exclusivamente por conducción. Valores entre uno y 10 sugieren un flujo laminar o slug flow, caracterizado por un movimiento fluido y ordenado. Por otro lado, un número de Nusselt mayor implica una convección más activa, asociada generalmente con un flujo turbulento, que suele encontrarse en el rango de 100 a 1000.

Al ser un número adimensional, está estrechamente relacionado con el número de Rayleigh del fluido. Además, existe una medida similar para los cuerpos sólidos, conocida como el número de Biot, que se enfoca en la conductividad térmica de sólidos en lugar de fluidos. En el contexto de la transferencia de masa, el análogo del número de Nusselt es el número de Sherwood, que desempeña un papel equivalente en el análisis de la transferencia de masa en fluidos. Y puede decirse además que al número de Nusselt es para la capa límite térmica lo que el coeficiente de fricción es para la capa límite de velocidad.

Este concepto es esencial para ingenieros y científicos en el diseño y análisis de sistemas de transferencia de calor, ofreciendo una herramienta valiosa para optimizar procesos y equipos en diversas aplicaciones industriales o de investigación.

HSD

Definición formal

El número de Nusselt es la relación entre la transferencia de calor por convección y la conductiva a través de un límite. Los flujos de calor por convección y conducción son paralelos entre sí y a la superficie normal de la superficie límite, y son todos perpendiculares al flujo de fluido medio en el caso simple.

NuL=Transferencia de calor convectivaTransferencia de calor conductiva=hk/L=hLk{displaystyle mathrm {Nu} {fnMicroc {mbox{Convective heat transfer # {mbox{Transferencia de calor conductiva }={frac {h}{k/L}={frac} {hL}{k}}

{displaystyle mathrm {Nu} _{L}={frac {mbox{Convective heat transfer }}{mbox{Conductive heat transfer }}}={frac {h}{k/L}}={frac {hL}{k}}}

donde h es el coeficiente de transferencia de calor por convección del flujo, L es la longitud característica y k es la conductividad térmica del flujo. líquido.

La selección de la longitud característica debe estar en la dirección del crecimiento (o el espesor) de la capa de límites; algunos ejemplos de longitud característica son: el diámetro exterior de un cilindro en (externo) flujo de la cruz (perpendicular al eje del cilindro), la longitud de una placa vertical sometida a convección natural, o el diámetro de una esfera. Para formas complejas, la longitud puede definirse como el volumen del cuerpo fluido dividido por la superficie.
La conductividad térmica del fluido es típicamente (pero no siempre) evaluada a la temperatura de la película, que para fines de ingeniería se puede calcular como el promedio de la temperatura del fluido a granel y la temperatura superficial de la pared.

En contraste con la definición anterior, conocida como número promedio de Nusselt, el número de Nusselt local se define tomando la longitud como la distancia desde el límite de la superficie hasta el punto de interés local.

Nux=hxxk{displaystyle mathrm {Nu} - ¿Qué? {h_{x}x} {k}}}

{displaystyle mathrm {Nu} _{x}={frac {h_{x}x}{k}}}

El número media, o promedio, se obtiene integrando la expresión sobre el rango de interés, como:

Nū ̄ =1L∫ ∫ 0LhxdxLk=h̄ ̄ Lk{displaystyle {fnMicrom} {Nu} }={frac {frac {1}{L}int ¿Qué? {fnMicrosoft Sans Serif} {}L}{k}} {}}}

{displaystyle {overline {mathrm {Nu} }}={frac {{frac {1}{L}}int _{0}^{L}h_{x} dx L}{k}}={frac {{overline {h}}L}{k}}}

Contexto

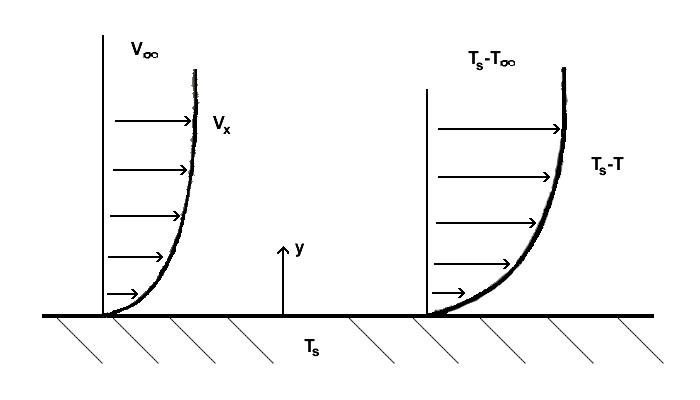
Es necesario comprender las capas límite de la convección para comprender la transferencia de calor por convección entre una superficie y un fluido que pasa por ella. Se desarrolla una capa límite térmica si la temperatura de la corriente libre de fluido y las temperaturas de la superficie difieren. Existe un perfil de temperatura debido al intercambio de energía resultante de esta diferencia de temperatura.

Thermal Boundary Layer

La tasa de transferencia de calor se puede escribir usando la ley de enfriamiento de Newton como

QSí.=hA()Ts- - TJUEGO JUEGO ){displaystyle ¿Qué?

{displaystyle Q_{y}=hAleft(T_{s}-T_{infty }right)}

donde h es el coeficiente de transferencia de calor y A es el área superficial de transferencia de calor. Debido a que la transferencia de calor en la superficie es por conducción, la misma cantidad se puede expresar en términos de la conductividad térmica k:

QSí.=− − kA∂ ∂ ∂ ∂ Sí.()T− − Ts)SilencioSí.=0{displaystyle Q_{y}=-kA{frac {partial }{partial Y}izquierda.

{displaystyle Q_{y}=-kA{frac {partial }{partial y}}left.left(T-T_{s}right)right|_{y=0}}

Estos dos términos son iguales; de este modo

− − kA∂ ∂ ∂ ∂ Sí.()T− − Ts)SilencioSí.=0=hA()Ts− − TJUEGO JUEGO ){displaystyle -kA{frac {partial }{partial Y}izquierda.

{displaystyle -kA{frac {partial }{partial y}}left.left(T-T_{s}right)right|_{y=0}=hAleft(T_{s}-T_{infty }right)}

Reorganización,

hk=∂ ∂ ()Ts− − T)∂ ∂ Sí.SilencioSí.=0()Ts− − TJUEGO JUEGO ){displaystyle {frac {fnh}={frac {left.{frac {partial left(T_{s}-Tright)}{partial y}}right_{y=0}{left(T_{infty }}}}}}}}}}}}}} {f}}}}}} {

{displaystyle {frac {h}{k}}={frac {left.{frac {partial left(T_{s}-Tright)}{partial y}}right|_{y=0}}{left(T_{s}-T_{infty }right)}}}

Al multiplicar por una longitud representativa L se obtiene una expresión adimensional:

hLk=\partial \partial ()Ts- - T)\partial \partial Sí.SilencioSí.=0()Ts- - TJUEGO JUEGO )L{fnMicroc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {nMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc {fnMicroc} {fnMicrosoft}}}}} {f}}}}} {f}}}}}} {f}}}}}}}}} {f} {f}f}}}}}}}}}}}f} {f} {f}f}}f}}f} {f}f}f} {f} {f}}f}}}}}f}f}f}f}f}f}}f}f}}f}}f}f}f}f}f}f}f}}}}}f}

{displaystyle {frac {hL}{k}}={frac {left.{frac {partial left(T_{s}-Tright)}{partial y}}right|_{y=0}}{frac {left(T_{s}-T_{infty }right)}{L}}}}

El lado derecho es ahora la relación entre el gradiente de temperatura en la superficie y el gradiente de temperatura de referencia, mientras que el lado izquierdo es similar al módulo de Biot. Esto se convierte en la relación entre la resistencia térmica conductiva y la resistencia térmica convectiva del fluido, también conocida como el número de Nusselt, Nu.

Nu=hk/L=hLk{displaystyle mathrm {Nu} ={frac} {h}{k/L}={frac} {hL}{k}}

{displaystyle mathrm {Nu} ={frac {h}{k/L}}={frac {hL}{k}}}

Derivación

El número de Nusselt se puede obtener mediante un análisis adimensional de la ley de Fourier, ya que es igual al gradiente de temperatura adimensional en la superficie:

q=- - kASilencio Silencio T{displaystyle q=-kAnabla T}

q=-kAnabla T

, donde q es la tasa de transferencia de calor, k es la conductividad térmica constante y T la temperatura del fluido.

De hecho, si:

Silencio Silencio .=LSilencio Silencio {displaystyle nabla 'Lnabla }

${displaystyle nabla '=Lnabla }$ y

T.=T− − ThTh− − Tc{displaystyle T'={frac {T-T_{h} {T-T_{c}}

${displaystyle T'={frac {T-T_{h}}{T_{h}-T_{c}}}}$

Llegamos a

- - Silencio Silencio .T.=LkA()Th- - Tc)q=hLk{displaystyle - ¿Qué? {hL}{k}}

{displaystyle -nabla 'T'={frac {L}{kA(T_{h}-T_{c})}}q={frac {hL}{k}}}

entonces definimos

NuL=hLk{displaystyle mathrm {Nu} - ¿Qué? {hL}{k}}

mathrm {Nu} _{L}={frac {hL}{k}}

así que la ecuación se convierte en

NuL=- - Silencio Silencio .T.{displaystyle mathrm {Nu} ¿Qué?

mathrm {Nu} _{L}=-nabla 'T'

Al integrarse sobre la superficie del cuerpo:

Nū ̄ =− − 1S.∫ ∫ S.NudS.{displaystyle {overline {mathrm {Nu} - Sí. {Nu} ,mathrm {d} S'!

${overline {mathrm {Nu} }}=-{{1} over {S'}}int _{S'}^{}mathrm {Nu} ,mathrm {d} S'!$ ,

Donde

S.=SL2{displaystyle S'={frac {S}{L^{2}}}

$S'={frac {S}{L^{2}}}$ .

Correlaciones empíricas

Normalmente, para la convección libre, el número de Nusselt promedio se expresa como una función del número de Rayleigh y el número de Prandtl, escrito como:

Nu=f()Ra,Pr){displaystyle mathrm {Nu} =f(mathrm {Ra}mathrm {Pr}}}

{displaystyle mathrm {Nu} =f(mathrm {Ra}mathrm {Pr})}

De lo contrario, para la convección forzada, el número de Nusselt generalmente es una función del número de Reynolds y el número de Prandtl, o

Nu=f()Re,Pr){displaystyle mathrm {Nu} =f(mathrm {Re}mathrm {Pr}}

{displaystyle mathrm {Nu} =f(mathrm {Re}mathrm {Pr})}

Existen correlaciones empíricas para una amplia variedad de geometrías que expresan el número de Nusselt en las formas antes mencionadas.

Convección libre

Convección libre en una pared vertical

Citado como proveniente de Churchill y Chu:

Nū ̄ L=0,688+0.663RaL1/4[1+()0.492/Pr)9/16]4/9RaL≤ ≤ 108{displaystyle {overline {mathrm {Nu} }_{L} =0.68+{frac {0.663,mathrm {Ra} ################################################################################################################################################################################################################################################################ - ¿Qué?

{displaystyle {overline {mathrm {Nu} }}_{L} =0.68+{frac {0.663,mathrm {Ra} _{L}^{1/4}}{left[1+(0.492/mathrm {Pr})^{9/16},right]^{4/9},}}quad mathrm {Ra} _{L}leq 10^{8}}

Convección libre desde placas horizontales

Si la longitud característica está definida

L=AsP{displaystyle L ={frac {fnK}} {fn}}} {fn}}}} {fn}}}}} {f}}}}}}} {fn}}}}}} {fn}}}}}}} {f}}}} {}}}}}}}} {}}}}}} {}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}

L ={frac {A_{s}}{P}}

Donde

As{displaystyle mathrm {A} _{s}

$mathrm {A} _{s}$ es la superficie de la placa y

P{displaystyle P}

$P$ es su perímetro.

Entonces, para la superficie superior de un objeto caliente en un ambiente más frío o la superficie inferior de un objeto frío en un ambiente más caliente

Nū ̄ L=0,544RaL1/4104≤ ≤ RaL≤ ≤ 107{displaystyle {overline {mathrm {Nu} }_{L} =0.54,mathrm {Ra} ¿Por qué? ¿Qué?

{overline {mathrm {Nu} }}_{L} =0.54,mathrm {Ra} _{L}^{1/4},quad 10^{4}leq mathrm {Ra} _{L}leq 10^{7}

Nū ̄ L=0.15RaL1/3107≤ ≤ RaL≤ ≤ 1011{displaystyle {overline {mathrm {Nu} }_{L} =0.15,mathrm {Ra} ¿Por qué? ¿Qué?

{overline {mathrm {Nu} }}_{L} =0.15,mathrm {Ra} _{L}^{1/3},quad 10^{7}leq mathrm {Ra} _{L}leq 10^{11}

Y para la superficie inferior de un objeto caliente en un ambiente más frío o la superficie superior de un objeto frío en un ambiente más caliente

Nū ̄ L=0,522RaL1/5105≤ ≤ RaL≤ ≤ 1010{displaystyle {overline {mathrm {Nu} }_{L} =0.52,mathrm {Ra} ¿Por qué? ¿Qué?

{displaystyle {overline {mathrm {Nu} }}_{L} =0.52,mathrm {Ra} _{L}^{1/5},quad 10^{5}leq mathrm {Ra} _{L}leq 10^{10}}

Convección forzada en placa plana

Placa plana en flujo laminar

El número local de Nusselt para el flujo laminar sobre una placa plana, a una distancia

x{displaystyle x}

$x$ abajo desde el borde de la placa, se da por

Nux=0.332Rex1/2Pr1/3,()Pr■0.6){displaystyle mathrm {Nu} _{x}.332,mathrm {Re} ¿Por qué?

mathrm {Nu} _{x} =0.332,mathrm {Re} _{x}^{1/2},mathrm {Pr} ^{1/3},(mathrm {Pr} >0.6)

El número promedio de Nusselt para el flujo laminar sobre una placa plana, desde el borde de la placa a una distancia aguas abajo

x{displaystyle x}

$x$ , se da por

Nū ̄ x=2⋅ ⋅ 0.332Rex1/2Pr1/3=0.664Rex1/2Pr1/3,()Pr■0.6){displaystyle {overline {mathrm {Nu} }_{x} ={2}cdot 0.332,mathrm {Re} ################################################################################################################################################################################################################################################################ ¿Por qué?

{displaystyle {overline {mathrm {Nu} }}_{x} ={2}cdot 0.332,mathrm {Re} _{x}^{1/2},mathrm {Pr} ^{1/3} =0.664,mathrm {Re} _{x}^{1/2},mathrm {Pr} ^{1/3},(mathrm {Pr} >0.6)}

Esfera en flujo convectivo

En algunas aplicaciones, como la evaporación de gotas esféricas de líquido en el aire, se utiliza la siguiente correlación:

NuD=2+0,4ReD1/2Pr1/3{displaystyle mathrm {Nu} _{D} ={2}+0.4,mathrm {Re} ¿Qué?

{displaystyle mathrm {Nu} _{D} ={2}+0.4,mathrm {Re} _{D}^{1/2},mathrm {Pr} ^{1/3},}

Convección forzada en flujo de tubería turbulento

Correlación de Gnielinski

Correlación de Gnielinski para flujo turbulento en tubos:

NuD=()f/8)()ReD− − 1000)Pr1+12.7()f/8)1/2()Pr2/3− − 1){displaystyle mathrm {Nu} _{D}={frac {left(f/8right)left(mathrm {Re} ¿Por qué?

mathrm {Nu} _{D}={frac {left(f/8right)left(mathrm {Re} _{D}-1000right)mathrm {Pr} }{1+12.7(f/8)^{1/2}left(mathrm {Pr} ^{2/3}-1right)}}

donde f es el factor de fricción de Darcy que puede obtenerse del gráfico de Moody o para tubos lisos de la correlación desarrollada por Petukhov:

f=()0,79In⁡ ⁡ ()ReD)− − 1.64)− − 2{displaystyle f=left(0.79lnleft(mathrm) [Re] _{D}right)-1.64right)^{-2}

f=left(0.79ln left(mathrm {Re} _{D}right)-1.64right)^{-2}

La correlación de Gnielinski es válida para:

0.5\leq \leq Pr\leq \leq 2000{displaystyle 0.5leq mathrm {Pr} leq 2000}

0.5leq mathrm {Pr} leq 2000

3000≤ ≤ ReD≤ ≤ 5× × 106{displaystyle 3000leq mathrm [Re] _{D}leq 5times 10^{6}

3000leq mathrm {Re} _{D}leq 5times 10^{6}

Ecuación de Dittus-Boelter

La ecuación de Dittus-Boelter (para flujo turbulento) tal como la introdujo W.H. McAdams es una función explícita para calcular el número de Nusselt. Es fácil de resolver pero es menos preciso cuando hay una gran diferencia de temperatura en el fluido. Está diseñado para tubos lisos, por lo que se recomienda su uso para tubos rugosos (la mayoría de las aplicaciones comerciales). La ecuación de Dittus-Boelter es:

NuD=0,023ReD4/5Prn{displaystyle mathrm {Nu} _{D}=0.023,mathrm {Re} _{D}^{4/5},mathrm {Pr}

mathrm {Nu} _{D}=0.023,mathrm {Re} _{D}^{4/5},mathrm {Pr} ^{n}

donde:

D{displaystyle D}

D

es el diámetro interior del conducto circular

Pr{displaystyle mathrm {Pr}

mathrm {Pr}

es el número de Prandtl

n=0,4{displaystyle n=0.4}

n=0.4

para el líquido que se calienta, y

n=0.3{displaystyle n=0.3}

n=0.3

para el líquido enfriado.

La ecuación de Dittus-Boelter es válida para

0.6\leq \leq Pr\leq \leq 160{displaystyle 0.6leq mathrm {Pr} leq 160}

0.6leq mathrm {Pr} leq 160

ReD≳ ≳ 10000{displaystyle mathrm {Re} _{D}gtrsim 10,000}

mathrm {Re} _{D}gtrsim 10,000

LD≳ ≳ 10{displaystyle {frac}gtrsim 10}

{frac {L}{D}}gtrsim 10

La ecuación Dittus-Boelter es una buena aproximación donde las diferencias de temperatura entre el fluido a granel y la superficie de transferencia de calor son mínimas, evitando la complejidad de la ecuación y la solución iterativa. Tomar agua con una temperatura media de fluido a granel de 20 °C (68 °F), viscosidad 10.07×10⁻⁴Pa.s y una temperatura superficial de transferencia de calor de 40 °C (104 °F) (viscosidad 6.96×10⁻⁴Pa.s, un factor de corrección de viscosidad

()μ μ /μ μ s){displaystyle ({mu }/{mu _{s}}}}

$({mu }/{mu _{s}})$ se puede obtener como 1.45. Esto aumenta a 3.57 con una temperatura superficial de transferencia de calor de 100 °C (212 °F) (viscosidad) 2.82×10⁻⁴Pa.s), haciendo una diferencia significativa al número Nusselt y el coeficiente de transferencia de calor.

Correlación Sieder-Tate

La correlación Sieder-Tate para el flujo turbulento es una función implícita, ya que analiza el sistema como un problema de valor límite no lineal. El resultado de Sieder-Tate puede ser más preciso ya que tiene en cuenta el cambio de viscosidad (

μ μ {displaystyle mu }

$mu$ y

μ μ s{displaystyle mu _{s}}

$mu _{s}$ ) debido al cambio de temperatura entre la temperatura promedio del fluido de vracs y la temperatura de la superficie de transferencia de calor, respectivamente. La correlación Sieder-Tate se resuelve normalmente por un proceso iterativo, ya que el factor de viscosidad cambiará a medida que el número Nusselt cambie.

NuD=0,027ReD4/5Pr1/3()μ μ μ μ s)0.14{displaystyle mathrm {Nu} _{D}=0.027,mathrm {Re} ¿Por qué?

mathrm {Nu} _{D}=0.027,mathrm {Re} _{D}^{4/5},mathrm {Pr} ^{1/3}left({frac {mu }{mu _{s}}}right)^{0.14}

donde:

μ μ {displaystyle mu }

mu

es la viscosidad del fluido a la temperatura del fluido a granel

μ μ s{displaystyle mu _{s}}

mu _{s}

es la viscosidad del fluido a la temperatura de la superficie del límite de transferencia de calor

La correlación Sieder-Tate es válida para

0.7\leq \leq Pr\leq \leq 16700{displaystyle 0.7leq mathrm {Pr} leq 16,700}

0.7leq mathrm {Pr} leq 16,700

ReD≥ ≥ 10000{displaystyle mathrm {Re} _{D}gq 10,000}

{displaystyle mathrm {Re} _{D}geq 10,000}

LD≳ ≳ 10{displaystyle {frac}gtrsim 10}

{frac {L}{D}}gtrsim 10

Convección forzada en flujo de tubería laminar completamente desarrollado

Para un flujo laminar interno completamente desarrollado, los números de Nusselt tienden hacia un valor constante para tuberías largas.

Para flujo interno:

Nu=hDhkf{displaystyle mathrm {Nu} ={frac} {hD_{h}{k_{f}}} {hD_} {h} {h} {h} {h} {h}} {h} {h}}}} {h} {h}}}} {h} {h} {h} {h} {h} {h}}}} {h} {h}}} {h} {h}} {h}}}}}}}} {h}}}}}}}}}}}}} {h} {h} {h} {h} {h} {h} {h} {h} {h} {h} {h} {h}} {h} {h} {h}}}}}}}} {h} {h}}}} {h}}}} {h}}}}} {h} {h} {h}}}}} {h}}}}} {h}}} {h}}}}}}}}}}} {h}}}} {h}}}}} {h}}}} {h} {h}}}}

mathrm {Nu} ={frac {hD_{h}}{k_{f}}}

donde:

D_h = Diámetro hidráulico

k_f = conductividad térmica del fluido

h = coeficiente de transferencia de calor convectivo

Convección con temperatura uniforme para tubos circulares

De Incropera & DeWitt,

NuD=3.66{displaystyle mathrm {Nu} _{D}=3.66}

mathrm {Nu} _{D}=3.66

OEIS secuencia A282581 da este valor como

NuD=3.6567934577632923619...{displaystyle mathrm {Nu} ¿Qué?

${displaystyle mathrm {Nu} _{D}=3.6567934577632923619...}$ .

Convección con flujo de calor uniforme para tubos circulares

Para el caso de flujo de calor superficial constante,

NuD=4.36{displaystyle mathrm {Nu} _{D}=4.36}

{displaystyle mathrm {Nu} _{D}=4.36}

Número de Nusselt

Definición formal

Contexto

Derivación

Correlaciones empíricas

Convección libre

Convección libre en una pared vertical

Convección libre desde placas horizontales

Placa plana en flujo laminar

Esfera en flujo convectivo

Convección forzada en flujo de tubería turbulento

Correlación de Gnielinski

Ecuación de Dittus-Boelter

Correlación Sieder-Tate

Convección forzada en flujo de tubería laminar completamente desarrollado

Convección con temperatura uniforme para tubos circulares

Convección con flujo de calor uniforme para tubos circulares

Calor latente

Constante de Stefan-Boltzmann

Transformación de la energía