Modus ponens

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Imágen de la representación formal del modus ponens — Representación formal del modus ponens

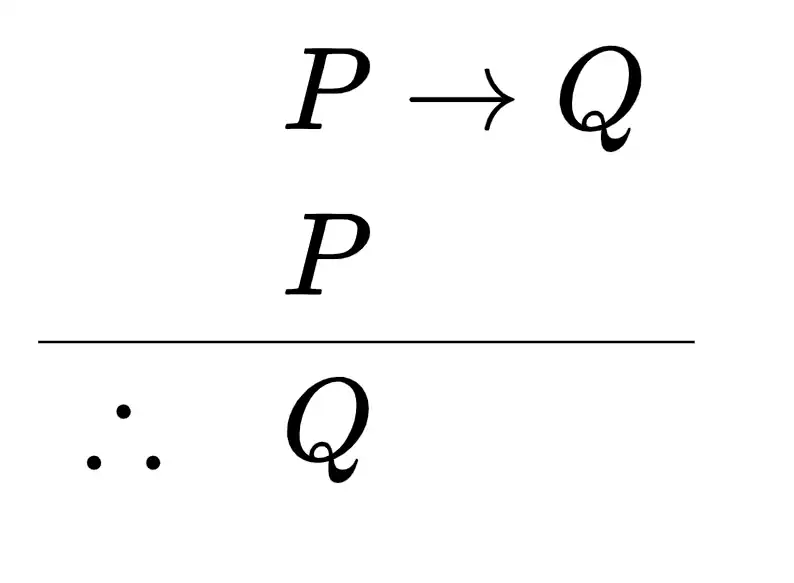
El modus ponens (MP), también conocido como modus ponendo ponens (del latín: modo que pone por posición) es una regla de inferencia deductiva de lógica proposicional. Este método representa una forma clásica de argumento deductivo donde: "Si P implica Q, cuando P es verdadero, entonces Q también debe ser verdadero". Esta regla permite establecer nuevas conclusiones a partir de las mismas premisas.

El modus ponens posee una estrecha relación con el modus tollens, otro tipo de argumento deductivo válido. Aunque ambos comparten una estructura similar, es importante no confundirlos con formas inválidas de argumentación, como "afirmar el consecuente", "negar el antecedente" o "evidencia de ausencia". Además, el dilema constructivo puede considerarse como una versión disyuntiva del modus ponens, y el silogismo hipotético a menudo se asocia con este, llegando a ser denominado en ocasiones como "doble modus ponens".

Si P implica Q, cuando P es verdadero, entonces Q también debe ser verdadero

La historia del modus ponens se remonta a la antigüedad, siendo Teofrasto uno de los primeros en describir explícitamente esta forma de argumento. Junto con el modus tollens, el modus ponens constituye uno de los patrones de inferencia más estándar y fundamentales en la lógica. Su aplicación es crucial para derivar cadenas de conclusiones lógicas que conducen a la meta del argumentador.

HSD

Explicación

La forma de un argumento modus ponens se asemeja a un silogismo, con dos premisas y una conclusión:

Si P, entonces Q.
pag _
Por lo tanto, Q.

La primera premisa es una afirmación condicional ("si-entonces"), es decir, que P implica Q. La segunda premisa es una afirmación de que P, el antecedente de la afirmación condicional, es el caso. De estas dos premisas se puede concluir lógicamente que Q, el consecuente de la afirmación condicional, también debe ser el caso.

Un ejemplo de un argumento que se ajusta a la forma modus ponens:

Si hoy es martes, entonces John irá a trabajar.
Hoy es martes.
Por lo tanto, John irá a trabajar.

Este argumento es válido, pero no influye en si alguna de las afirmaciones del argumento es realmente verdadera; para que modus ponens sea un argumento sólido, las premisas deben ser verdaderas para cualquier instancia verdadera de la conclusión. Un argumento puede ser válido pero, sin embargo, poco sólido si una o más premisas son falsas; si un argumento es válido y todas las premisas son verdaderas, entonces el argumento es sólido. Por ejemplo, John podría ir a trabajar el miércoles. En este caso, el razonamiento de que John va a trabajar (porque es miércoles) no es sólido. El argumento solo es sólido los martes (cuando John va a trabajar), pero válido todos los días de la semana. Se dice que un argumento proposicional que usa modus ponens es deductivo.

En los cálculos secuenciales de conclusión única, el modus ponens es la regla de corte. El teorema de eliminación de corte para un cálculo dice que toda prueba que involucre a Corte puede transformarse (generalmente, por un método constructivo) en una prueba sin Corte, y por lo tanto, ese Corte es admisible.

La correspondencia de Curry-Howard entre demostraciones y programas relaciona el modus ponens con la aplicación de funciones: si f es una función de tipo P → Q y x es de tipo P, entonces fx es de tipo Q.

En inteligencia artificial, el modus ponens a menudo se denomina encadenamiento hacia adelante.

Notación formal

La regla modus ponens se puede escribir en notación secuencial como $Pa Q,; PAGS;; vdash;; q$

donde P, Q y P → Q son declaraciones (o proposiciones) en un lenguaje formal y ⊢ es un símbolo metalógico que significa que Q es una consecuencia sintáctica de P y P → Q en algún sistema lógico.

Justificación mediante tabla de verdad

La validez del modus ponens en la lógica clásica de dos valores se puede demostrar claramente mediante el uso de una tabla de verdad.

pags	q	pag → q
T	T	T
T	F	F
F	T	T
F	F	T

En instancias de modus ponens asumimos como premisas que p → q es verdadera y p es verdadera. Solo una línea de la tabla de verdad, la primera, satisface estas dos condiciones (p y p → q). En esta línea, q también es cierto. Por lo tanto, siempre que p → q sea verdadera y p sea verdadera, q también debe ser verdadera.

Modus Ponens en la lógica actual

Si bien modus ponens es una de las formas de argumento más utilizadas en lógica, no debe confundirse con una ley lógica; más bien, es uno de los mecanismos aceptados para la construcción de pruebas deductivas que incluye la "regla de definición" y la "regla de sustitución". Modus ponens permite eliminar una declaración condicional de una prueba o argumento lógico (los antecedentes) y, por lo tanto, no llevar estos antecedentes hacia adelante en una cadena de símbolos cada vez más larga; por esta razón modus ponens a veces se llama la regla del desapego o la ley del desapego. Enderton, por ejemplo, observa que "el modus ponens puede producir fórmulas más cortas a partir de fórmulas más largas", y Russell observa que "el proceso de la inferencia no puede reducirse a símbolos. Su único registro es la ocurrencia de ⊦q [el consecuente]... una inferencia es la eliminación de una premisa verdadera; es la disolución de una implicación"..

Una justificación para la "confianza en la inferencia es la creencia de que si las dos afirmaciones anteriores [los antecedentes] no están equivocadas, la afirmación final [el consecuente] no está equivocada". En otras palabras: si una declaración o proposición implica una segunda, y la primera declaración o proposición es verdadera, entonces la segunda también lo es. Si P implica Q y P es verdadera, entonces Q es verdadera.

Correspondencia con otros marcos matemáticos

Cálculo de probabilidades

Modus ponens representa una instancia de la Ley de probabilidad total que para una variable binaria se expresa como:

${displaystyle Pr(Q)=Pr(Qmid P)Pr(P)+Pr(Qmid lnot P)Pr(lnot P),}$ ,

donde eg ${ estilo de visualización Pr (Q)}$ denota la probabilidad de $q$ y la probabilidad condicional ${ estilo de visualización Pr (Q mid P)}$ generaliza la implicación lógica $P a Q$ . Asuma que ${ estilo de visualización Pr (Q) = 1}$ es equivalente a $q$ ser VERDADERO, y eso ${ estilo de visualización Pr (Q) = 0}$ es equivalente a $q$ ser FALSO. Entonces es fácil ver que ${ estilo de visualización Pr (Q) = 1}$ cuando ${ estilo de visualización Pr (Q mid P) = 1}$ y ${ estilo de visualización Pr (P) = 1}$ . Por lo tanto, la ley de probabilidad total representa una generalización del modus ponens.

Lógica subjetiva

Modus ponens representa una instancia del operador de deducción binomial en lógica subjetiva expresada como:

${displaystyle omega_{Q|P}^{A}=(omega_{Q|P}^{A},omega_{Q|lnot P}^{A})circledcirc omega _ {P}^{A},}$ ,

donde ${displaystyle omega_{P}^{A}}$ denota la opinión subjetiva acerca $PAGS$ de lo expresado por la fuente $A$ , y la opinión condicional ${displaystyle omega_{Q|P}^{A}}$ generaliza la implicación lógica $P a Q$ . La opinión marginal deducida acerca de $q$ se denota por ${displaystyle omega_{Q|P}^{A}}$ . El caso donde ${displaystyle omega_{P}^{A}}$ hay una opinión absolutamente VERDADERA sobre $PAGS$ es equivalente a que la fuente $A$ diga que $PAGS$ es VERDADERO, y el caso donde ${displaystyle omega_{P}^{A}}$ hay una opinión absoluta FALSA sobre $PAGS$ es equivalente a que la fuente $A$ diga que $PAGS$ es FALSO. El operador ${displaystyle circledcirc}$ de deducción de la lógica subjetiva produce una opinión deducida VERDADERA absoluta ${displaystyle omega_{Q|P}^{A}}$ cuando la opinión condicional ${displaystyle omega_{Q|P}^{A}}$ es VERDADERA absoluta y la opinión antecedente ${displaystyle omega_{P}^{A}}$ es absolutamente VERDADERO. Por lo tanto, la deducción lógica subjetiva representa una generalización tanto del modus ponens como de la Ley de probabilidad total.

Supuestos casos de falla

Los filósofos y lingüistas han identificado una variedad de casos en los que el modus ponens parece fallar. Vann McGee, por ejemplo, argumentó que modus ponens puede fallar para condicionales cuyos consecuentes son ellos mismos condicionales. Lo siguiente es un ejemplo:

Ya sea Shakespeare o Hobbes escribieron Hamlet.
Si Shakespeare o Hobbes escribieron Hamlet, entonces si Shakespeare no lo hizo, Hobbes lo hizo.
Por lo tanto, si Shakespeare no escribió Hamlet, Hobbes lo hizo.

Dado que Shakespeare escribió Hamlet, la primera premisa es cierta. La segunda premisa también es cierta, ya que partiendo de un conjunto de posibles autores se limita a Shakespeare y Hobbes y eliminando a uno de ellos se deja solo al otro. Sin embargo, la conclusión puede parecer falsa, ya que descartar a Shakespeare como autor de Hamlet dejaría numerosos candidatos posibles, muchos de ellos alternativas más plausibles que Hobbes.

La forma general de los contraejemplos al modus ponens tipo McGee es simplemente ${displaystyle P,Prightarrow (Qrightarrow R)}$ , por lo tanto ${ estilo de visualización Q flecha derecha R}$ ; no es imprescindible que $PAGS$ sea una disyunción, como en el ejemplo dado. Que este tipo de casos constituyan fallas del modus ponens sigue siendo un punto de vista controvertido entre los lógicos, pero las opiniones varían sobre cómo se deben desechar los casos.

En lógica deóntica, algunos ejemplos de obligación condicional también plantean la posibilidad de falla modus ponens. Estos son casos en los que la premisa condicional describe una obligación basada en una acción inmoral o imprudente, por ejemplo, "Si Doe asesina a su madre, debe hacerlo con delicadeza", para lo cual la dudosa conclusión incondicional sería "Doe debe asesinar con delicadeza a su madre". madre." Parecería seguir que si Doe de hecho está asesinando suavemente a su madre, entonces por modus ponens está haciendo exactamente lo que debería, incondicionalmente, estar haciendo. Una vez más, el fracaso del modus ponens no es un diagnóstico popular, pero a veces se argumenta a favor.

Posibles falacias

La falacia de afirmar el consecuente es una mala interpretación común del modus ponens.

Contenido relacionado

Más resultados...