Modus tollens

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Representación formal del *modus tollens*

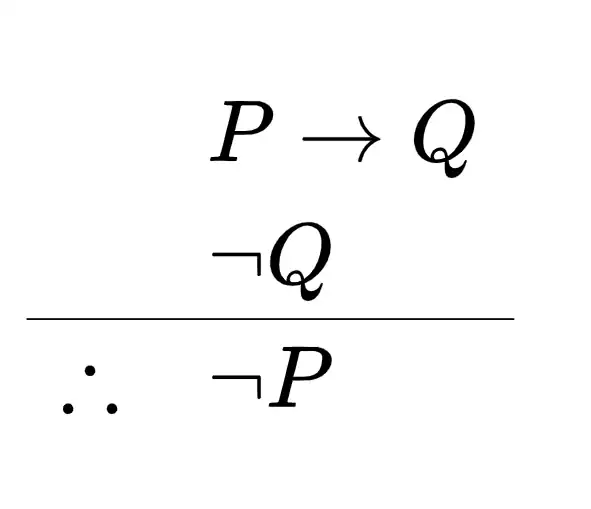
El modus tollens conocido también como modus tollendo tollens es una regla de inferencia lógica en forma de argumento deductivo que llega a una conclusión negativa por la negación de una premisa cuando existe una relación de causalidad. Esta forma de argumento deductivo se estructura de la siguiente manera: "Si P a Q, y no Q, por lo tanto, no P". La frase modus tollendo tollens proviene del latín: "método de quitar quitando". El modus tollens se conoce también como negación del consecuente.

La estructura del modus tollens subraya una verdad lógica fundamental: si un enunciado es verdadero, su contrapositivo también lo es. O en otras palabras, la inferencia de que P implica siempre Q lleva a que la negación de Q implique la negación de P, constituyendo a priori un argumento válido.

El modus tollens está intrínsecamente vinculado con el modus ponens, otra regla de inferencia lógica fundamental. Sin embargo, es crucial diferenciarlo de dos formas de argumentación también similares pero inválidas: la afirmación del consecuente y la negación del antecedente. Además, es importante considerar su relación con conceptos como la contraposición y la prueba por contrapositiva.

La historia de esta construcción lógica se remonta a la Grecia antigua, siendo Teofrasto uno de los primeros en describir explícitamente esta forma argumental. Su estudio es relevante para la comprensión de la deducción lógica, y para aquellos interesados en la filosofía, las matemáticas y la ciencia en general.

HSD

Explicación

La forma de un argumento modus tollens se asemeja a un silogismo, con dos premisas y una conclusión:

Si P, entonces Q.

No Q.

Por lo tanto, no P.

La primera premisa es una afirmación condicional ("si-entonces"), como P implica Q. La segunda premisa es una afirmación de que Q, el consecuente de la afirmación condicional, no es el caso. De estas dos premisas se puede concluir lógicamente que P, el antecedente de la afirmación condicional, tampoco es el caso.

Por ejemplo:

Si el perro detecta un intruso, el perro ladrará.

El perro no ladraba.

Por lo tanto, ningún intruso fue detectado por el perro.

Suponiendo que ambas premisas sean verdaderas (el perro ladrará si detecta un intruso y, de hecho, no ladra), se deduce que no se ha detectado ningún intruso. Este es un argumento válido ya que no es posible que la conclusión sea falsa si las premisas son verdaderas. (Es concebible que haya habido un intruso que el perro no detectó, pero eso no invalida el argumento; la primera premisa es "si el perro detecta un intruso" Lo importante es que el perro detecte o no un intruso, no si lo hay.)

Otro ejemplo:

Si soy el asesino del hacha, entonces puedo usar un hacha.

No puedo usar un hacha.

Por lo tanto, no soy el asesino del hacha.

Otro ejemplo:

Si Rex es un pollo, entonces es un pájaro.

Rex no es un pájaro.

Por lo tanto, Rex no es un pollo.

Relación con el modus ponens

Cada uso de modus tollens puede convertirse en un uso de modus ponens y un uso de transposición a la premisa, lo cual es una implicación material. Por ejemplo:

Si P, entonces Q. (premise – implicación material)

Si no Q, entonces no P. (derived by transposition)

No Q. (premise)

Por lo tanto, no P. (derived by modus ponens)

Del mismo modo, cada uso de modus ponens puede convertirse en un uso de modus tollens y transposición.

Notación formal

La regla modus tollens se puede establecer formalmente como:

{frac {Pto Q,neg Q}{therefore neg P}}

Donde $Pto Q$ significa la declaración "P implica Q". $neg Q$ significa "no es el caso que Q" (o en breve "no Q"). Entonces, cuando sea " $Pto Q$ "y" $neg Q$ " cada uno aparece por sí mismo como una línea de una prueba, luego " $neg P$ " se puede colocar válidamente en una línea posterior.

La regla modus tollens se puede escribir en notación secuencial:

Pto Q,neg Qvdash neg P

Donde $vdash$ es un símbolo metalógico que significa que $neg P$ es una consecuencia sintáctica de $Pto Q$ y $neg Q$ en algún sistema lógico;

o como el enunciado de una tautología funcional o teorema de lógica proposicional:

{displaystyle ((Pto Q)land neg Q)to neg P}

Donde $P$ y $Q$ son propuestas expresadas en algún sistema formal;

o incluyendo suposiciones:

{frac {Gamma vdash Pto Q~~~Gamma vdash neg Q}{Gamma vdash neg P}}

aunque dado que la regla no cambia el conjunto de suposiciones, esto no es estrictamente necesario.

A menudo se ven reescrituras más complejas que implican modus tollens, por ejemplo, en la teoría de conjuntos:

Psubseteq Q

xnotin Q

therefore xnotin P

("P es un subconjunto de Q. x no está en Q. Por lo tanto, x no está en P.")

También en lógica de predicados de primer orden:

forall x:~P(x)to Q(x)

{displaystyle neg Q(y)}

{displaystyle therefore ~neg P(y)}

("Para todo x si x es P entonces x es Q. y no es Q. Por lo tanto, y no es P.")

Estrictamente hablando, estas no son instancias de modus tollens, pero pueden derivarse de modus tollens siguiendo algunos pasos adicionales.

Justificación mediante tabla de verdad

La validez del modus tollens se puede demostrar claramente a través de una tabla de verdad.

p	q	p → q
T	T	T
T	F	F
F	T	T
F	F	T

En instancias de modus tollens asumimos como premisas que p → q es verdadera y q es falsa. Solo hay una línea de la tabla de verdad, la cuarta línea, que satisface estas dos condiciones. En esta línea, p es falsa. Por lo tanto, en todos los casos en que p → q es verdadera y q es falsa, p también debe ser falsa.

Prueba formal

Vía silogismo disyuntivo

Paso	Proposición	Derivación
1	$Prightarrow Q$	Dado
2	$neg Q$	Dado
3	${displaystyle neg Plor Q}$	implicación material (1)
4	$neg P$	Syllogismo disjuntivo (3,2)

Vía reducción al absurdo

Paso	Proposición	Derivación
1	$Prightarrow Q$	Dado
2	$neg Q$	Dado
3	$P$	Assumption
4	$Q$	Modus ponens (1,3)
5	${displaystyle Qland neg Q}$	Introducción de la orden (2,4)
6	$neg P$	Reductio ad absurdum (3,5)
7	${displaystyle neg Qrightarrow neg P}$	Introducción condicional (2,6)

Por contraposición

Paso	Proposición	Derivación
1	$Prightarrow Q$	Dado
2	$neg Q$	Dado
3	${displaystyle neg Qrightarrow neg P}$	Contraposición (1)
4	$neg P$	Modus ponens (2,3)

Correspondencia con otros marcos matemáticos

Cálculo de probabilidades

Modus tollens representa una instancia de la ley de probabilidad total combinada con Bayes' teorema expresado como:

${displaystyle Pr(P)=Pr(Pmid Q)Pr(Q)+Pr(Pmid lnot Q)Pr(lnot Q),}$ ,

donde los condicionales ${displaystyle Pr(Pmid Q)}$ y ${displaystyle Pr(Pmid lnot Q)}$ se obtiene con (la forma extendida de) el teorema de Bayes expresado como:

${displaystyle Pr(Pmid Q)={frac {Pr(Qmid P),a(P)}{Pr(Qmid P),a(P)+Pr(Qmid lnot P),a(lnot P)}};;;}$ y ${displaystyle ;;;Pr(Pmid lnot Q)={frac {Pr(lnot Qmid P),a(P)}{Pr(lnot Qmid P),a(P)+Pr(lnot Qmid lnot P),a(lnot P)}}}$ .

En las ecuaciones anteriores ${displaystyle Pr(Q)}$ denota la probabilidad de $Q$ , y ${displaystyle a(P)}$ denota la tasa de base (aka. probabilidad anterior) de $P$ . La probabilidad condicional ${displaystyle Pr(Qmid P)}$ generaliza la declaración lógica $Pto Q$ , es decir, además de asignar TRUE o FALSE también podemos asignar cualquier probabilidad a la declaración. Supongamos que ${displaystyle Pr(Q)=1}$ equivale a $Q$ y eso ${displaystyle Pr(Q)=0}$ equivale a $Q$ ser FALSE. Entonces es fácil ver que ${displaystyle Pr(P)=0}$ cuando ${displaystyle Pr(Qmid P)=1}$ y ${displaystyle Pr(Q)=0}$ . Esto es porque ${displaystyle Pr(lnot Qmid P)=1-Pr(Qmid P)=0}$ así ${displaystyle Pr(Pmid lnot Q)=0}$ en la última ecuación. Por lo tanto, los términos del producto en la primera ecuación siempre tienen un factor cero para que ${displaystyle Pr(P)=0}$ que equivale a $P$ ser FALSE. Por lo tanto, la ley de probabilidad total combinada con el teorema de Bayes representa una generalización de modus tollens.

Lógica subjetiva

Modus tollens representa una instancia del operador de abducción en lógica subjetiva expresada como:

${displaystyle omega _{P{tilde {|}}Q}^{A}=(omega _{Q|P}^{A},omega _{Q|lnot P}^{A}){widetilde {circledcirc }}(a_{P},,omega _{Q}^{A}),}$ ,

Donde ${displaystyle omega _{Q}^{A}}$ denota la opinión subjetiva sobre $Q$ , y ${displaystyle (omega _{Q|P}^{A},omega _{Q|lnot P}^{A})}$ denota un par de opiniones binomiales condicionales, expresadas por fuente $A$ . El parámetro ${displaystyle a_{P}}$ denota la tasa de base (aka. la probabilidad anterior) de $P$ . La opinión marginal abducida sobre $P$ es denotado ${displaystyle omega _{P{tilde {|}}Q}^{A}}$ . La opinión condicional ${displaystyle omega _{Q|P}^{A}}$ generaliza la declaración lógica $Pto Q$ , es decir, además de asignar TRUE o FALSE la fuente $A$ puede asignar cualquier opinión subjetiva a la declaración. El caso donde ${displaystyle omega _{Q}^{A}}$ es una opinión absoluta TRUE es equivalente a la fuente $A$ diciendo que $Q$ es TRUE, y el caso donde ${displaystyle omega _{Q}^{A}}$ es una opinión absoluta FALSE es equivalente a la fuente $A$ diciendo que $Q$ Es FALSE. The abduction operator ${displaystyle {widetilde {circledcirc }}}$ la lógica subjetiva produce una opinión abducida FALSE absoluta ${displaystyle omega _{P{widetilde {|}}Q}^{A}}$ cuando la opinión condicional ${displaystyle omega _{Q|P}^{A}}$ es TRUE absoluto y la opinión consiguiente ${displaystyle omega _{Q}^{A}}$ es FALSE absoluto. Por lo tanto, el secuestro subjetivo de lógica representa una generalización de ambos modus tollens y de la Ley de probabilidad total combinada con el teorema de Bayes.

Contenido relacionado

Más resultados...