Método del cuadrado medio

En matemáticas e informática, el método del cuadrado medio es un método para generar números pseudoaleatorios. En la práctica es un método muy defectuoso para muchos propósitos prácticos, ya que su período suele ser muy corto y tiene algunas debilidades graves; repetido suficientes veces, el método del cuadrado medio comenzará a generar repetidamente el mismo número o pasará a un número anterior en la secuencia y se repetirá indefinidamente.

Historia

En matemáticas

El método fue inventado por John von Neumann y descrito por él en una conferencia en 1949.

En la charla de 1949, Von Neumann bromeó diciendo que "Cualquiera que considere métodos aritméticos para producir dígitos aleatorios está, por supuesto, en un estado de pecado". Lo que quiso decir, explicó, fue que no había verdaderos "números aleatorios", sólo medios para producirlos, y "un procedimiento aritmético estricto", como el método del cuadrado medio. #34;no es ese método". Sin embargo, descubrió que estos métodos eran cientos de veces más rápidos que leer textos "verdaderos". números aleatorios de tarjetas perforadas, que tenían importancia práctica para su trabajo en ENIAC. Encontró la "destrucción" Las secuencias de cuadrados medios son un factor a su favor, porque pueden detectarse fácilmente: "siempre se teme la aparición de ciclos cortos no detectados". Nicholas Metropolis informó secuencias de 750.000 dígitos antes de la "destrucción" mediante el uso de números de 38 bits con el "cuadrado medio" método.

El libro Los dados rotos de Ivar Ekeland ofrece un relato detallado de cómo el método fue inventado por un fraile franciscano conocido sólo como el hermano Edvin en algún momento entre 1240 y 1250. Supuestamente, el manuscrito ahora está perdido., pero Jorge Luis Borges le envió a Ekeland una copia que hizo en la Biblioteca del Vaticano.

La modificación del algoritmo del cuadrado medio con una secuencia de Weyl mejora el período y la aleatoriedad.

El método

Para generar una secuencia de números pseudoaleatorios de n dígitos, se crea un valor inicial de n dígitos y se eleva al cuadrado, produciendo un valor de 2n. -dígito. Si el resultado tiene menos de 2n dígitos, se añaden ceros a la izquierda para compensar. Los n dígitos del medio del resultado serían el siguiente número de la secuencia y se devolverían como resultado. Luego, este proceso se repite para generar más números.

El valor de n debe ser incluso para que el método funcione – si el valor de n es extraño, entonces no habrá necesariamente un "middle" único n- dígitos para seleccionar. Considere lo siguiente: Si un número de 3 dígitos es cuadrado, puede producir un número de 6 dígitos (por ejemplo, 540)² = 291600). Si hubiera 3 dígitos medios, eso dejaría 6 − 3 = 3 dígitos que se distribuirían a la izquierda y a la derecha del medio. Es imposible distribuir uniformemente estos dígitos a ambos lados del número medio, y por lo tanto no hay " dígitos medio". Es aceptable acolchar las semillas con ceros a la izquierda para crear un valor n- Número de dígitos (por ejemplo, 540 → 0540).

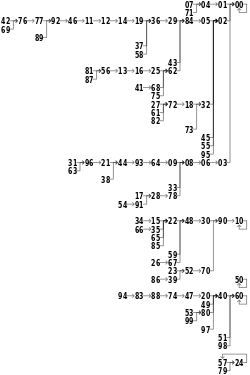
Para un generador de números de ndígitos, el período no puede ser superior a 8ⁿ. Si los n dígitos del medio son todos ceros, el generador genera ceros para siempre. Si la primera mitad de un número en la secuencia es cero, los números siguientes disminuirán hasta cero. Si bien estas corridas de cero son fáciles de detectar, ocurren con demasiada frecuencia para que este método sea de uso práctico. El método del medio cuadrado también puede atascarse en un número distinto de cero. Para n = 4, esto ocurre con los valores 0100, 2500, 3792 y 7600. Otros valores semilla forman ciclos repetitivos muy cortos, por ejemplo, 0540 → 2916 → 5030 → 3009. Estos fenómenos son aún más obvio cuando n = 2, ya que ninguna de las 100 semillas posibles genera más de 14 iteraciones sin volver a 0, 10, 50, 60 o un bucle 24 ↔ 57.

Ejemplo de implementación

Aquí, el algoritmo se representa en Python 3.11.

seed_number = int()entrada()"Por favor ingrese un número de cuatro dígitos:n[######])Número = seed_numberya_seen = set()contra = 0mientras Número no dentro ya_seen: contra += 1 ya_seen.añadir()Número) Número = int()str()Número * Número).zfill()8[2:6]) # zfill añade relleno de ceros impresión()f"#{}contra}: {}Número}")impresión()f"Comenzamos con {}seed_number} y f"nos han repetido después {}contra} pasos" fcon {}Número}.")