Mediana

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En estadística y teoría de la probabilidad, la mediana es el valor que separa la mitad superior de la mitad inferior de una muestra de datos, una población o una distribución de probabilidad. Para un conjunto de datos, puede considerarse como el valor "del medio". La característica básica de la mediana en la descripción de datos en comparación con la media (que sería más bien como un promedio "promedio") es que no está sesgada por una pequeña proporción de valores extremadamente grandes o pequeños y, por lo tanto, proporciona una mejor representación de un valor tipo. El ingreso medio (calculado por mediana), por ejemplo, puede ser una mejor manera de sugerir qué es un ingreso "típico", porque la distribución del ingreso puede ser muy sesgada. La mediana tiene una importancia central en las estadísticas robustas, ya que es la estadística más resistente, con un punto de ruptura del 50 %: siempre que no más de la mitad de los datos estén contaminados.

Conjunto de datos finitos de números

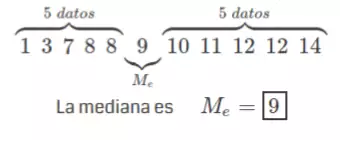
La mediana de una lista finita de números es el número "medio", cuando esos números se enumeran en orden de menor a mayor.

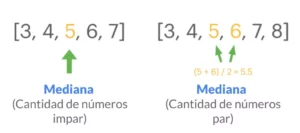
Si el conjunto de datos tiene un número impar de observaciones, se selecciona la del medio. Por ejemplo, la siguiente lista de siete números,1, 3, 3, 6, 7, 8, 9 tiene la mediana de 6, que es el cuarto valor.

Si el conjunto de datos tiene un número par de observaciones, no hay un valor medio distinto y la mediana generalmente se define como la media aritmética de los dos valores medios. Por ejemplo, este conjunto de datos de 8 números1, 2, 3, 4, 5, 6, 8, 9

tiene un valor mediano de 4.5, es decir ${\ estilo de visualización (4+5)/2}$ . (En términos más técnicos, esto interpreta la mediana como el rango medio totalmente recortado).

En general, con esta convención, la mediana se puede definir de la siguiente manera: Para un conjunto de datos $X$ de $norte$ elementos, ordenados de menor a mayor, Si $norte$ es impar, $\mathrm {mediana} (x)=x_{(n+1)/2}$ Si $norte$ incluso, $\mathrm {mediana} (x)={\frac {x_{(n/2)}+x_{(n/2)+1}}{2}}$

\scriptstyle {\bar {x}}={\frac {1}{n}}\sum_{{i=1}}^{n}x_{i}

Escribe	Descripción	Ejemplo	Resultado
Significado aritmetico	Suma de valores de un conjunto de datos dividida por el número de valores: $\scriptstyle {\bar {x}}={\frac {1}{n}}\sum_{{i=1}}^{n}x_{i}$	(1 + 2 + 2 + 3 + 4 + 7 + 9) / 7	4
Mediana	Valor medio que separa las mitades mayor y menor de un conjunto de datos	1, 2, 2, 3, 4, 7, 9	3
Modo	Valor más frecuente en un conjunto de datos	1, 2, 2, 3, 4, 7, 9	2

Definicion formal

Formalmente, la mediana de una población es cualquier valor tal que, como máximo, la mitad de la población es menor que la mediana propuesta y, como máximo, la mitad es mayor que la mediana propuesta. Como se vio anteriormente, las medianas pueden no ser únicas. Si cada conjunto contiene menos de la mitad de la población, entonces parte de la población es exactamente igual a la mediana única.

La mediana está bien definida para cualquier dato ordenado (unidimensional) y es independiente de cualquier métrica de distancia. Por lo tanto, la mediana se puede aplicar a clases clasificadas pero no numéricas (por ejemplo, calculando una calificación mediana cuando los estudiantes se califican de A a F), aunque el resultado puede estar a mitad de camino entre las clases si hay un número par de casos.

Una mediana geométrica, por otro lado, se define en cualquier número de dimensiones. Un concepto relacionado, en el que el resultado está obligado a corresponder a un miembro de la muestra, es el medoide.

No existe una notación estándar ampliamente aceptada para la mediana, pero algunos autores representan la mediana de una variable x como x͂ o como μ _1/2, a veces también como M. En cualquiera de estos casos, el uso de estos u otros símbolos para la mediana debe definirse explícitamente cuando se introduzcan.

La mediana es un caso especial de otras formas de resumir los valores típicos asociados con una distribución estadística: es el 2.º cuartil, el 5.º decil y el 50.º percentil.

Usos

La mediana se puede utilizar como una medida de ubicación cuando se concede poca importancia a los valores extremos, normalmente porque una distribución está sesgada, los valores extremos no se conocen o los valores atípicos no son fiables, es decir, pueden ser errores de medición/transcripción.

Por ejemplo, considere el conjunto múltiple1, 2, 2, 2, 3, 14.

La mediana es 2 en este caso (como lo es la moda), y podría verse como una mejor indicación del centro que la media aritmética de 4, que es mayor que todos menos uno de los valores. Sin embargo, la relación empírica ampliamente citada de que la media se desplaza "más hacia la cola" de una distribución que la mediana generalmente no es cierta. A lo sumo, se puede decir que las dos estadísticas no pueden estar "demasiado alejadas"; ver § Medias y medianas relacionadas con la desigualdad a continuación.

Como una mediana se basa en los datos intermedios de un conjunto, no es necesario conocer el valor de los resultados extremos para calcularlo. Por ejemplo, en una prueba de psicología que investiga el tiempo necesario para resolver un problema, si un pequeño número de personas no pudo resolver el problema en absoluto en el tiempo dado, aún se puede calcular una mediana.

Debido a que la mediana es simple de entender y fácil de calcular, además de ser una aproximación robusta a la media, la mediana es una estadística de resumen popular en las estadísticas descriptivas. En este contexto, hay varias opciones para una medida de variabilidad: el rango, el rango intercuartílico, la desviación absoluta media y la desviación absoluta mediana.

A efectos prácticos, a menudo se comparan diferentes medidas de ubicación y dispersión sobre la base de qué tan bien se pueden estimar los valores de población correspondientes a partir de una muestra de datos. La mediana, estimada a partir de la mediana muestral, tiene buenas propiedades en este sentido. Si bien no suele ser óptimo si se supone una distribución de población determinada, sus propiedades siempre son razonablemente buenas. Por ejemplo, una comparación de la eficiencia de los estimadores candidatos muestra que la media de la muestra es estadísticamente más eficiente cuando, y solo cuando, los datos no están contaminados por datos de distribuciones de colas pesadas o mezclas de distribuciones. Incluso entonces, la mediana tiene una eficiencia del 64 % en comparación con la media de varianza mínima (para muestras normales grandes), lo que significa que la varianza de la mediana será ~50 % mayor que la varianza de la media.

Distribuciones de probabilidad

Para cualquier distribución de probabilidad de valor real con función de distribución acumulativa F, una mediana se define como cualquier número real m que satisface las desigualdades $\int _{(-\infty ,m]}dF(x)\geq {\frac {1}{2}}{\text{ and }}\int _{[m,\infty )}dF (x)\geq {\frac{1}{2}}$ .

Una redacción equivalente utiliza una variable aleatoria X distribuida según F : $\operatorname {P} (X\leq m)\geq {\frac {1}{2}}{\text{ y }}\operatorname {P} (X\geq m)\geq {\frac { 1}{2}}$

Tenga en cuenta que esta definición no requiere que X tenga una distribución absolutamente continua (que tiene una función de densidad de probabilidad ƒ ), ni requiere una distribución discreta. En el primer caso, las desigualdades se pueden actualizar a la igualdad: una mediana satisface $\operatorname {P} (X\leq m)=\int _{-\infty}^{m}{f(x)\,dx}={\frac {1}{2}}=\int _{m}^{\infty }{f(x)\,dx}=\nombre del operador {P} (X\geq m)$ .

Cualquier distribución de probabilidad en R tiene al menos una mediana, pero en casos patológicos puede haber más de una mediana: si F es constante 1/2 en un intervalo (de modo que ƒ =0 allí), entonces cualquier valor de ese intervalo es un mediana.

Medianas de distribuciones particulares

Las medianas de ciertos tipos de distribuciones se pueden calcular fácilmente a partir de sus parámetros; además, existen incluso para algunas distribuciones que carecen de una media bien definida, como la distribución de Cauchy:

La mediana de una distribución unimodal simétrica coincide con la moda.
La mediana de una distribución simétrica que posee una media μ también toma el valor μ.
- La mediana de una distribución normal con media μ y varianza σ es μ. De hecho, para una distribución normal, media = mediana = moda.
- La mediana de una distribución uniforme en el intervalo [ a, b ] es ( a + b ) / 2, que también es la media.
La mediana de una distribución de Cauchy con parámetro de ubicación x ₀ y parámetro de escala y es x ₀, el parámetro de ubicación.
La mediana de una distribución de ley de potencia x, con exponente a > 1 es 2 x _min, donde x _min es el valor mínimo para el que se cumple la ley de potencia
La mediana de una distribución exponencial con parámetro de tasa λ es el logaritmo natural de 2 dividido por el parámetro de tasa: λ ln 2.
La mediana de una distribución de Weibull con parámetro de forma k y parámetro de escala λ es λ (ln 2).

Poblaciones

Propiedad de optimalidad

El error absoluto medio de una variable real c con respecto a la variable aleatoria X es $E(\izquierda|Xc\derecha|)\,$

Siempre que la distribución de probabilidad de X sea tal que exista la expectativa anterior, entonces m es una mediana de X si y solo si m es un minimizador del error absoluto medio con respecto a X. En particular, m es una mediana muestral si y solo si m minimiza la media aritmética de las desviaciones absolutas.

Más generalmente, una mediana se define como un mínimo de $E(|Xc|-|X|),$

como se analiza más adelante en la sección sobre medianas multivariadas (específicamente, la mediana espacial).

Esta definición de la mediana basada en la optimización es útil en el análisis de datos estadísticos, por ejemplo, en el agrupamiento de k -medianas.

Desigualdad que relaciona medias y medianas

Si la distribución tiene varianza finita, entonces la distancia entre la mediana ${\ tilde {X}}$ y la media ${\bar {X}}$ está acotado por una desviación estándar.

Este límite fue demostrado por Mallows, quien usó la desigualdad de Jensen dos veces, de la siguiente manera. Usando |·| para el valor absoluto, tenemos ${\begin{alineado}|\mu -m|=|\operatorname {E} (Xm)|&\leq \operatorname {E} (|Xm|)\\&\leq \operatorname {E} ( |X-\mu |)\\&\leq {\sqrt {\operatorname {E} \left((X-\mu )^{2}\right)}}=\sigma .\end{alineado}}$

La primera y la tercera desigualdades provienen de la desigualdad de Jensen aplicada a la función de valor absoluto ya la función del cuadrado, ambas convexas. La segunda desigualdad proviene del hecho de que una mediana minimiza la función de desviación absoluta $a\mapsto\operatorname {E} (|Xa|)$ .

La prueba de Mallows se puede generalizar para obtener una versión multivariada de la desigualdad simplemente reemplazando el valor absoluto con una norma: $\|\mu -m\|\leq {\sqrt {\operatorname {E} \left(\|X-\mu \|^{2}\right)}}={\sqrt {\operatorname { rastrear} \left(\nombre del operador {var} (X)\right)}}$

donde m es una mediana espacial, es decir, un minimizador de la función $a\mapsto\operatorname {E} (\|Xa\|).\,$ La mediana espacial es única cuando la dimensión del conjunto de datos es dos o más.

Una prueba alternativa utiliza la desigualdad de Chebyshev unilateral; aparece en una desigualdad en los parámetros de ubicación y escala. Esta fórmula también se sigue directamente de la desigualdad de Cantelli.

Distribuciones unimodales

Para el caso de distribuciones unimodales, se puede lograr un límite más definido en la distancia entre la mediana y la media: $\left|{\tilde {X}}-{\bar {X}}\right|\leq \left({\frac {3}{5}}\right)^{\frac {1}{ 2}}\sigma \aproximadamente 0,7746\sigma$ .

Una relación similar se da entre la mediana y la moda: $\left|{\tilde {X}}-\mathrm {modo} \right|\leq 3^{\frac {1}{2}}\sigma \approx 1,732\sigma .$

Desigualdad de Jensen para medianas

La desigualdad de Jensen establece que para cualquier variable aleatoria X con una expectativa finita E [ X ] y para cualquier función convexa f $f[E(x)]\leq E[f(x)]$

Esta desigualdad se generaliza a la mediana también. Decimos que una función f:ℝ→ℝ es una función C si, para cualquier t, $f^{-1}\left(\,(-\infty ,t]\,\right)=\{x\in \mathbb {R} \mid f(x)\leq t\}$

es un intervalo cerrado (permitiendo los casos degenerados de un solo punto o un conjunto vacío). Toda función convexa es una función C, pero no se cumple lo contrario. Si f es una función de C, entonces $f(\operatorname {Mediana} [X])\leq \operatorname {Mediana} [f(X)]$

Si las medianas no son únicas, el enunciado vale para la suprema correspondiente.

Medianas para muestras

En esta sección se analiza la teoría de la estimación de una mediana poblacional a partir de una muestra. Para calcular la mediana de una muestra "a mano", consulte § Conjunto de datos finitos de números anterior.

La mediana de la muestra

Cálculo eficiente de la mediana de la muestra

Aunque la clasificación por comparación de n elementos requiere operaciones Ω( n log n ), los algoritmos de selección pueden calcular el k -ésimo más pequeño de n elementos con solo operaciones Θ( n ). Esto incluye la mediana, que es lanorte/2estadístico de º orden (o para un número par de muestras, la media aritmética de los dos estadísticos de orden medio).

Los algoritmos de selección aún tienen la desventaja de requerir memoria Ω( n ), es decir, necesitan tener la muestra completa (o una porción de tamaño lineal) en la memoria. Debido a que esto, así como el requisito de tiempo lineal, puede ser prohibitivo, se han desarrollado varios procedimientos de estimación de la mediana. Una simple es la regla de la mediana de tres, que estima la mediana como la mediana de una submuestra de tres elementos; esto se usa comúnmente como una subrutina en el algoritmo de clasificación quicksort, que usa una estimación de la mediana de su entrada. Un estimador más robusto es el noveno de Tukey, que es la regla de la mediana de tres aplicada con recursividad limitada: si A es la muestra dispuesta como una matriz, ymed3( A ) = mediana( A [1], A [norte/2], A [ norte ]),

entoncesnoveno( A ) = med3(med3( A [1...1/3n ]), med3( A [1/3n...2/3n ]), med3( A [2/3n... n ]))

El remediador es un estimador de la mediana que requiere tiempo lineal pero memoria sublineal, operando en un solo paso sobre la muestra.

Distribución muestral

Laplace determinó las distribuciones tanto de la media muestral como de la mediana muestral. La distribución de la mediana muestral de una población con una función de densidad $f(x)$ es asintóticamente normal con media $metro$ y varianza ${\ fracción {1}{4nf(m)^{2}}}$

donde $metro$ es la mediana de $f(x)$ y $norte$ es el tamaño de la muestra. Una demostración moderna sigue a continuación. El resultado de Laplace ahora se entiende como un caso especial de la distribución asintótica de cuantiles arbitrarios.

Para muestras normales, la densidad es $f(m)=1/{\sqrt {2\pi \sigma ^{2}}}$ , por lo tanto, para muestras grandes, la varianza de la mediana es igual a $({\pi }/{2})\cdot (\sigma ^{2}/n).$ (Consulte también la sección #Eficiencia a continuación).

Derivación de la distribución asintótica

Tomamos el tamaño de la muestra como un número impar ${\ estilo de visualización N = 2n + 1}$ y supongamos nuestra variable continua; la fórmula para el caso de variables discretas se da a continuación en § Densidad local empírica. La muestra se puede resumir como "por debajo de la mediana", "en la mediana" y "por encima de la mediana", lo que corresponde a una distribución trinominal con probabilidades ${\ estilo de visualización F (v-1)}$ , ${\ estilo de visualización f (v)}$ y ${\ estilo de visualización 1-F (v)}$ . Para una variable continua, la probabilidad de que los valores de múltiples muestras sean exactamente iguales a la mediana es 0, por lo que se puede calcular la densidad de en el punto $v$ directamente de la distribución trinominal: $\Pr[\operatorname {Mediana} =v]\,dv={\frac {(2n+1)!}{n!n!}}F(v)^{n}(1-F(v ))^{n}f(v)\,dv$ .

Ahora introducimos la función beta. Para argumentos enteros $\beta$ , esto se puede expresar como $\mathrm {B} (\alpha ,\beta )={\frac {(\alpha -1)!(\beta -1)!}{(\alpha +\beta -1)!}}$ . Además, recuerda que ${\ estilo de visualización f (v) \, dv = dF (v)}$ . Usando estas relaciones y configurando ambas $\alfa$ y $\beta$ igual a $n+1$ permite que la última expresión se escriba como ${\frac {F(v)^{n}(1-F(v))^{n}}{\mathrm {B} (n+1,n+1)}}\,dF(v )$

Por lo tanto, la función de densidad de la mediana es una distribución beta simétrica impulsada por $F$ . Su media, como cabría esperar, es 0,5 y su varianza es ${\ estilo de visualización 1/(4 (N + 2))}$ . Por la regla de la cadena, la varianza correspondiente de la mediana muestral es ${\frac{1}{4(N+2)f(m)^{2}}}$ .

El 2 adicional es despreciable en el límite.

Densidad local empírica

En la práctica, las funciones $F$ y $F$ a menudo no se conocen o se suponen. Sin embargo, se pueden estimar a partir de una distribución de frecuencia observada. En esta sección damos un ejemplo. Considere la siguiente tabla, que representa una muestra de 3800 observaciones (de valor discreto):

v	0	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5
f(v)	0.000	0.008	0.010	0.013	0.083	0.108	0.328	0.220	0.202	0.023	0.005
F(v)	0.000	0.008	0.018	0.031	0.114	0.222	0.550	0.770	0.972	0.995	1.000

Debido a que las observaciones tienen valores discretos, construir la distribución exacta de la mediana no es una traducción inmediata de la expresión anterior para $\Pr(\operatorname {Mediana} =v)$ ; uno puede (y normalmente lo hace) tener múltiples instancias de la mediana en su muestra. Así que debemos sumar todas estas posibilidades: $\Pr(\operatorname {Mediana} =v)=\sum _{i=0}^{n}\sum _{k=0}^{n}{\frac {N!}{i!( Nik)!k!}}F(v-1)^{i}(1-F(v))^{k}f(v)^{Nik}$

Aquí, i es el número de puntos estrictamente menor que la mediana yk el número estrictamente mayor.

Usando estos preliminares, es posible investigar el efecto del tamaño de la muestra en los errores estándar de la media y la mediana. La media observada es 3,16, la mediana bruta observada es 3 y la mediana interpolada observada es 3,174. La siguiente tabla proporciona algunas estadísticas de comparación.

Tamaño de la muestraEstadística	3	9	15	21
Valor esperado de la mediana	3.198	3.191	3.174	3.161
Error estándar de la mediana (fórmula anterior)	0.482	0.305	0.257	0.239
Error estándar de la mediana (aproximación asintótica)	0.879	0.508	0.393	0.332
Error estándar de la media	0.421	0.243	0.188	0.159

El valor esperado de la mediana cae ligeramente a medida que aumenta el tamaño de la muestra mientras que, como era de esperar, los errores estándar tanto de la mediana como de la media son proporcionales a la raíz cuadrada inversa del tamaño de la muestra. La aproximación asintótica peca de precavida al sobrestimar el error estándar.

Estimación de la varianza a partir de datos muestrales

El valor de $(2f(x))^{-2}$ —el valor asintótico de $n^{-{\frac {1}{2}}}(\nu -m)$ donde $\nu$ es la mediana de la población— ha sido estudiada por varios autores. El método jackknife estándar "eliminar uno" produce resultados inconsistentes. Una alternativa, el método "eliminar k", donde $k$ crece con el tamaño de la muestra se ha demostrado que es asintóticamente consistente. Este método puede ser computacionalmente costoso para grandes conjuntos de datos. Se sabe que una estimación bootstrap es consistente, pero converge muy lentamente (orden de $n^{-{\frac {1}{4}}}$ ). Se han propuesto otros métodos pero su comportamiento puede diferir entre muestras grandes y pequeñas.

Eficiencia

La eficiencia de la mediana muestral, medida como el cociente entre la varianza de la media y la varianza de la mediana, depende del tamaño de la muestra y de la distribución de la población subyacente. Para una muestra de tamaño $N=2n+1$ de la distribución normal, la eficiencia para N grande es ${\frac {2}{\pi}}{\frac {N+2}{N}}$

La eficiencia tiende a ${\frac{2}{\pi }}$ como $norte$ tiende al infinito.

En otras palabras, la varianza relativa de la mediana será ${\ estilo de visualización \ pi /2 \ aproximadamente 1,57}$ , o 57% mayor que la varianza de la media, el error estándar relativo de la mediana será $(\pi /2)^{\frac {1}{2}}\aprox. 1,25$ , o 25% mayor que el error estándar de la media, ${\ estilo de visualización \ sigma / {\ sqrt {n}}}$ (ver también la sección #Distribución del muestreo arriba).

Otros estimadores

Para distribuciones univariadas que son simétricas con respecto a una mediana, el estimador de Hodges-Lehmann es un estimador robusto y altamente eficiente de la mediana de la población.

Si los datos están representados por un modelo estadístico que especifica una familia particular de distribuciones de probabilidad, entonces se pueden obtener estimaciones de la mediana ajustando esa familia de distribuciones de probabilidad a los datos y calculando la mediana teórica de la distribución ajustada. La interpolación de Pareto es una aplicación de esto cuando se supone que la población tiene una distribución de Pareto.

Mediana multivariada

Anteriormente, este artículo discutió la mediana univariada, cuando la muestra o población tenía una dimensión. Cuando la dimensión es dos o más, existen múltiples conceptos que amplían la definición de mediana univariante; cada una de esas medianas multivariadas concuerda con la mediana univariada cuando la dimensión es exactamente uno.

Mediana marginal

La mediana marginal se define para vectores definidos con respecto a un conjunto fijo de coordenadas. Una mediana marginal se define como el vector cuyas componentes son medianas univariadas. La mediana marginal es fácil de calcular y sus propiedades fueron estudiadas por Puri y Sen.

Mediana geométrica

La mediana geométrica de un conjunto discreto de puntos muestrales $x_{1},\ldots x_{N}$ en un espacio euclidiano es el punto que minimiza la suma de las distancias a los puntos muestrales. ${\hat {\mu }}={\underset {\mu \in \mathbb {R} ^{m}}{\operatorname {arg\,min} }}\sum _{n=1}^ {N}\izquierda\|\mu -x_{n}\derecha\|_{2}$

A diferencia de la mediana marginal, la mediana geométrica es equivariante con respecto a las transformaciones de similitud euclidiana, como traslaciones y rotaciones.

Mediana en todas las direcciones

Si las medianas marginales de todos los sistemas de coordenadas coinciden, su ubicación común puede denominarse "mediana en todas las direcciones". Este concepto es relevante para la teoría del voto debido al teorema del votante medio. Cuando existe, la mediana en todas las direcciones coincide con la mediana geométrica (al menos para distribuciones discretas).

Punto central

Una generalización alternativa de la mediana en dimensiones superiores es el punto central.

Otros conceptos relacionados con la mediana

Mediana interpolada

Cuando se trata de una variable discreta, a veces es útil considerar los valores observados como puntos medios de intervalos continuos subyacentes. Un ejemplo de esto es una escala de Likert, en la que se expresan opiniones o preferencias en una escala con un número determinado de respuestas posibles. Si la escala consta de números enteros positivos, una observación de 3 podría considerarse como la representación del intervalo de 2,50 a 3,50. Es posible estimar la mediana de la variable subyacente. Si, digamos, el 22 % de las observaciones tienen un valor de 2 o menos y el 55,0 % tienen un valor de 3 o menos (por lo que el 33 % tiene un valor de 3), entonces la mediana $metro$ es 3 ya que la mediana es el valor más pequeño de $X$ para cual $F(x)$ es mayor que la mitad. Pero la mediana interpolada está entre 2,50 y 3,50. Primero sumamos la mitad del ancho del intervalo $w$ a la mediana para obtener el límite superior del intervalo de la mediana. Luego restamos la proporción del ancho del intervalo que es igual a la proporción del 33% que se encuentra por encima de la marca del 50%. En otras palabras, dividimos el ancho del intervalo proporcionalmente al número de observaciones. En este caso, el 33 % se divide en un 28 % por debajo de la mediana y un 5 % por encima de ella, por lo que restamos 5/33 del ancho del intervalo del límite superior de 3,50 para obtener una mediana interpolada de 3,35. Más formalmente, si los valores $f(x)$ son conocidos, la mediana interpolada se puede calcular a partir de $m_{\text{int}}=m+w\left[{\frac {1}{2}}-{\frac {F(m)-{\frac {1}{2}}}{ f(m)}}\derecha].$

Alternativamente, si en una muestra observada hay $k$ puntajes por encima de la categoría mediana, $j$ puntuaciones en él y $I$ puntajes por debajo de él, entonces la mediana interpolada está dada por $m_{\text{int}}=m-{\frac {w}{2}}\left[{\frac {ki}{j}}\right].$

Pseudo-mediana

Para distribuciones univariadas que son simétricas con respecto a una mediana, el estimador de Hodges-Lehmann es un estimador robusto y altamente eficiente de la mediana de la población; para distribuciones no simétricas, el estimador de Hodges-Lehmann es un estimador robusto y altamente eficiente de la pseudomediana de la población, que es la mediana de una distribución simetrizada y que está cerca de la mediana de la población. El estimador de Hodges-Lehmann se ha generalizado a distribuciones multivariadas.

Variantes de regresión

El estimador de Theil-Sen es un método de regresión lineal robusta basado en la búsqueda de medianas de pendientes.

Filtro mediano

El filtro mediano es una herramienta importante del procesamiento de imágenes, que puede eliminar de manera efectiva cualquier ruido de sal y pimienta de las imágenes en escala de grises.

Análisis de conglomerados

En el análisis de conglomerados, el algoritmo de conglomerado de k-medianas proporciona una forma de definir conglomerados, en el que el criterio de maximizar la distancia entre las medias de los conglomerados que se utiliza en el agrupamiento de k-medias se reemplaza por maximizar la distancia entre las medianas de los conglomerados.

Línea mediana-mediana

Este es un método de regresión robusta. La idea se remonta a Wald en 1940, quien sugirió dividir un conjunto de datos bivariados en dos mitades según el valor del parámetro independiente. $X$ : una mitad izquierda con valores menores que la mediana y una mitad derecha con valores mayores que la mediana. Sugirió tomar los medios de los dependientes $y$ e independiente $X$ variables de las mitades izquierda y derecha y estimar la pendiente de la recta que une estos dos puntos. Luego, la línea podría ajustarse para que se ajuste a la mayoría de los puntos en el conjunto de datos.

Nair y Shrivastava en 1942 sugirieron una idea similar pero abogaron por dividir la muestra en tres partes iguales antes de calcular las medias de las submuestras. Brown y Mood en 1951 propusieron la idea de utilizar las medianas de dos submuestras en lugar de las medias. Tukey combinó estas ideas y recomendó dividir la muestra en tres submuestras de igual tamaño y estimar la línea con base en las medianas de las submuestras.

Estimadores imparciales de la mediana

Artículo principal: Sesgo de un estimador § Estimadores imparciales medianos

Cualquier estimador medio -insesgado minimiza el riesgo (pérdida esperada) con respecto a la función de pérdida de error cuadrático, según lo observado por Gauss. Un estimador insesgado de mediana minimiza el riesgo con respecto a la función de pérdida de desviación absoluta, como lo observó Laplace. Otras funciones de pérdida se utilizan en teoría estadística, particularmente en estadísticas robustas.

La teoría de los estimadores imparciales de la mediana fue revivida por George W. Brown en 1947:

Se dirá que una estimación de un parámetro unidimensional θ es medianamente insesgada si, para θ fijo, la mediana de la distribución de la estimación tiene el valor θ; es decir, la estimación subestima tan a menudo como sobrestima. Para la mayoría de los propósitos, este requisito parece lograr tanto como el requisito de imparcialidad media y tiene la propiedad adicional de que es invariante bajo la transformación uno a uno.— página 584

Se han informado otras propiedades de los estimadores imparciales de mediana. Los estimadores insesgados de mediana son invariantes bajo transformaciones uno a uno.

Existen métodos para construir estimadores de mediana insesgada que son óptimos (en un sentido análogo a la propiedad de varianza mínima para estimadores de media insesgada). Tales construcciones existen para distribuciones de probabilidad que tienen funciones de probabilidad monótonas. Uno de estos procedimientos es un análogo del procedimiento de Rao-Blackwell para estimadores medios no sesgados: el procedimiento se cumple para una clase más pequeña de distribuciones de probabilidad que el procedimiento de Rao-Blackwell, pero para una clase más grande de funciones de pérdida.

Contenido relacionado

Más resultados...