Maquina atwood

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Demostración de aulas utilizada para ilustrar los principios de la mecánica clásica

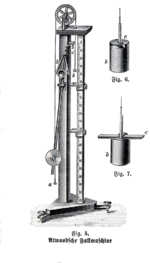
La máquina de Atwood (o máquina de Atwood) fue inventada en 1784 por el matemático inglés George Atwood como un experimento de laboratorio para verificar las leyes mecánicas del movimiento. con aceleración constante. La máquina de Atwood es una demostración común en el aula que se utiliza para ilustrar los principios de la mecánica clásica.

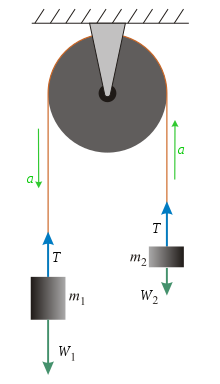
La máquina Atwood ideal consiste en dos objetos de masa $m 1$ y $m 2$ , conectado por una cadena inextensible sin masa sobre una polea ideal sin masa.

Ambas masas experimentan una aceleración uniforme. Cuando $m 1 = m 2$ , la máquina está en equilibrio neutro independientemente de la posición de los pesos.

Ecuación de aceleración constante

Los diagramas de cuerpo gratuitos de las dos masas colgantes de la máquina Atwood. Nuestra convención de firmas, representada por los vectores de aceleración es que $m 1$ se acelera hacia abajo y eso $m 2$ se acelera hacia arriba, como sería el caso si $m 1 ■ m 2$

Una ecuación para la aceleración se puede derivar mediante el análisis de fuerzas. Suponiendo una cuerda inextensible y sin masa y una polea ideal sin masa, las únicas fuerzas a considerar son: fuerza de tensión ( $T$ ), y el peso de las dos masas ( $W 1$ y $W 2$ ). Para encontrar una aceleración, considere las fuerzas que afectan a cada masa individual. Usando la segunda ley de Newton (con una convención de firmas) $m_{2}}" xmlns="http://www.w3.org/1998/Math/MathML">m1■m2{displaystyle m_{1} {2}m_{2}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert skin-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fe36df2b6f2ba500cbe0bc1c7be3962493b07c33" style="vertical-align: -0.671ex; width:9.288ex; height:2.176ex;"/>$ ) derivar un sistema de ecuaciones para la aceleración ( $a$ ).

Como convención de firmas, asuma que a es positivo cuando hacia abajo ${displaystyle m_{1}}$ y hacia arriba ${displaystyle m_{2}}$ . Peso de ${displaystyle m_{1}}$ y ${displaystyle m_{2}}$ es simplemente ${displaystyle W_{1}=m_{1}g}$ y ${displaystyle W_{2}=m_{2}g}$ respectivamente.

Fuerzas que afectan a m₁:

{displaystyle m_{1}g-T=m_{1}a}

₂

{displaystyle T-m_{2}g=m_{2}a}

{displaystyle m_{1}g-m_{2}g=m_{1}a+m_{2}a,}

{displaystyle a=g{frac {m_{1}-m_{2}}{m_{1}+m_{2}}}}

La máquina de Atwood se utiliza a veces para ilustrar el método lagrangiano de derivar ecuaciones de movimiento.

Ecuación de tensión

Puede resultar útil conocer una ecuación para la tensión en la cuerda. Para evaluar la tensión, sustituya la ecuación por aceleración en cualquiera de las dos ecuaciones de fuerza.

{displaystyle a=g{m_{1}-m_{2} over m_{1}+m_{2}}}

Por ejemplo, la sustitución en ${displaystyle m_{1}a=m_{1}g-T}$ , resultados en

{displaystyle T={2gm_{1}m_{2} over m_{1}+m_{2}}={2g over 1/m_{1}+1/m_{2}}=m_{h},g}

{displaystyle m_{h}={frac {2m_{1}m_{2}}{m_{1}+m_{2}}}}

{displaystyle m_{h}}

Ecuaciones para una polea con inercia y fricción

Para diferencias de masa muy pequeñas entre $m 1$ y $m 2$ , la inercia rotacional $I$ de la polea de radio $r$ no se puede pasar por alto. La aceleración angular de la polea está dada por la condición de no deslizamiento:

{displaystyle alpha ={frac {a}{r}},}

{displaystyle alpha }

{displaystyle tau _{mathrm {net} }=left(T_{1}-T_{2}right)r-tau _{mathrm {friction} }=Ialpha }

Combinando con la segunda ley de Newton para las masas colgantes, y resolviendo $T 1$ , $T 2$ , y $a$ , tenemos:

Aceleración:

{displaystyle a={{g(m_{1}-m_{2})-{tau _{mathrm {friction} } over r}} over {m_{1}+m_{2}+{{I} over {r^{2}}}}}}

Tensión en el segmento de cuerda más cercano a $m 1$ :

{displaystyle T_{1}={{m_{1}gleft(2m_{2}+{frac {I}{r^{2}}}+{frac {tau _{mathrm {friction} }}{rg}}right)} over {m_{1}+m_{2}+{frac {I}{r^{2}}}}}}

Tensión en el segmento de cuerda más cercano a $m 2$ :

{displaystyle T_{2}={{m_{2}gleft(2m_{1}+{frac {I}{r^{2}}}+{frac {tau _{mathrm {friction} }}{rg}}right)} over {m_{1}+m_{2}+{frac {I}{r^{2}}}}}}

Si la fricción del rodamiento fuera insignificante (pero no la inercia de la polea ni la tracción de la cuerda sobre el borde de la polea), estas ecuaciones se simplifican con los siguientes resultados:

Aceleración:

{displaystyle a={{gleft(m_{1}-m_{2}right)} over {m_{1}+m_{2}+{frac {I}{r^{2}}}}}}

Tensión en segmento de cuerda más cercano $m 1$ :

{displaystyle T_{1}={{m_{1}gleft(2m_{2}+{frac {I}{r^{2}}}right)} over {m_{1}+m_{2}+{frac {I}{r^{2}}}}}}

Tensión en el segmento de cuerda más cercano a $m 2$ :

{displaystyle T_{2}={{m_{2}gleft(2m_{1}+{frac {I}{r^{2}}}right)} over {m_{1}+m_{2}+{frac {I}{r^{2}}}}}}

Implementaciones prácticas

Las ilustraciones originales de Atwood muestran el eje de la polea principal apoyado sobre las llantas de otras cuatro ruedas, para minimizar las fuerzas de fricción de los cojinetes. Muchas implementaciones históricas de la máquina siguen este diseño.

Un ascensor con contrapeso se aproxima a una máquina Atwood ideal y, por tanto, libera al motor impulsor de la carga que supone sujetar la cabina del ascensor: sólo tiene que superar la diferencia de peso y la inercia de las dos masas. El mismo principio se aplica a los funiculares con dos vagones conectados sobre vías inclinadas, así como a los ascensores de la Torre Eiffel que se contrapesan entre sí. Los remontes son otro ejemplo, donde las góndolas se mueven sobre un sistema de poleas cerradas (continuas) hacia arriba y hacia abajo de la montaña. El remonte es similar al ascensor de contrapeso, pero con una fuerza de constricción proporcionada por el cable en la dimensión vertical, logrando así trabajo tanto en la dimensión horizontal como en la vertical. Los elevadores de botes son otro tipo de sistema de elevador con contrapeso que se aproxima a una máquina Atwood.

Contenido relacionado

Más resultados...