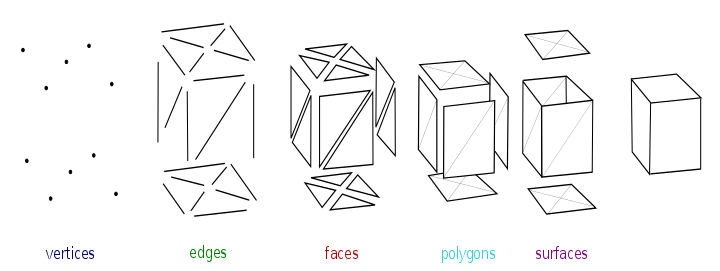
Malla poligonal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En gráficos por computadora 3D y modelado de sólidos, una malla poligonal es una colección de vértices, bordes y caras que define la forma de un objeto poliédrico. Las caras suelen consistir en triángulos (malla de triángulos), cuadriláteros (quads) u otros polígonos convexos simples (n-gonos), ya que esto simplifica la representación, pero también pueden estar compuestas de manera más general por polígonos cóncavos o incluso polígonos con agujeros.

El estudio de las mallas poligonales es un gran subcampo de los gráficos por computadora (específicamente gráficos por computadora en 3D) y el modelado geométrico. Se utilizan diferentes representaciones de mallas poligonales para diferentes aplicaciones y objetivos. La variedad de operaciones realizadas sobre mallas puede incluir: lógica booleana (geometría sólida constructiva), suavizado, simplificación y muchas otras. También existen algoritmos para trazado de rayos, detección de colisiones y dinámica de cuerpos rígidos con mallas poligonales. Si se representan los bordes de la malla en lugar de las caras, entonces el modelo se convierte en un modelo de estructura alámbrica.

Las mallas volumétricas se diferencian de las mallas poligonales en que representan explícitamente tanto la superficie como el volumen de una estructura, mientras que las mallas poligonales solo representan explícitamente la superficie (el volumen está implícito).

Existen varios métodos para la generación de mallas, incluido el algoritmo de cubos en marcha.

Elementos

Los objetos creados con mallas poligonales deben almacenar diferentes tipos de elementos. Estos incluyen vértices, aristas, caras, polígonos y superficies. En muchas aplicaciones, sólo se almacenan los vértices, aristas y caras o polígonos. Un renderizador puede admitir solo caras de 3 lados, por lo que se deben construir polígonos con muchas de ellas, como se muestra arriba. Sin embargo, muchos renderizadores admiten quads y polígonos de lados superiores, o pueden convertir polígonos en triángulos sobre la marcha, lo que hace innecesario almacenar una malla en forma triangulada.

vertex

Una posición (generalmente en espacio 3D) junto con otra información como las coordenadas de color, vector normal y textura.

borde

Una conexión entre dos vértices.

cara

Un conjunto cerrado de bordes, en el que cara triángulo tiene tres bordes, y un cara cuadrada tiene cuatro bordes. A poligonal es un conjunto de caras coplanar. En sistemas que soportan caras multi-sided, poligones y caras son equivalentes. Sin embargo, la mayoría de hardware de renderización soporta sólo caras de 3 o 4 caras, por lo que los polígonos están representados como múltiples caras. Matemáticamente una malla poligonal puede considerarse una cuadrícula no estructurada, o un gráfico no dirigido, con propiedades adicionales de geometría, forma y topología.

superficies

Más a menudo llamado grupos de alisamiento, son útiles, pero no necesarios para agrupar regiones lisas. Considere un cilindro con tapas, como una lata de soda. Para el afeitado suave de los lados, todas las normales de la superficie deben apuntar horizontalmente lejos del centro, mientras que las normales de las tapas deben apuntar directamente hacia arriba y hacia abajo. Rendered como una sola superficie confeccionada por Phong, los vértices de crease tendrían normales incorrectos. Por lo tanto, se necesita alguna manera de determinar dónde dejar de suavizar para agrupar partes lisas de una malla, al igual que los poligones grupo 3 caras. Como alternativa a proporcionar superficies/grupos de calma, una malla puede contener otros datos para calcular los mismos datos, como un ángulo de división (polígonos con normalidades por encima de este umbral se tratan automáticamente como grupos de licuado separados o alguna técnica como dividir o acarrear se aplica automáticamente al borde entre ellos). Además, las mallas de muy alta resolución están menos sujetas a cuestiones que requerirían grupos de suavizado, ya que sus polígonos son tan pequeños como para hacer la necesidad irrelevante. Además, existe otra alternativa en la posibilidad de simplemente separar las superficies mismas del resto de la malla. Los renderers no intentan lijar los bordes a través de polígonos no contiguos.

grupos

Algunos formatos de malla contienen grupos, que definen elementos separados de la malla, y son útiles para determinar subobjetos separados para la animación esquelética o actores separados para la animación no esquelética.

materiales

Generalmente materiales se definirá, permitiendo diferentes porciones de la malla para utilizar diferentes tonos cuando se renderice.

coordenadas UV

La mayoría de los formatos de malla también soportan alguna forma de coordenadas UV que son una representación separada 2d de la malla "desplegada" para mostrar qué parte de un mapa de textura 2-dimensional para aplicar a diferentes polígonos de la malla. También es posible que las mallas contengan otro vértice semejante atributo información como el color, vectores tangentes, mapas de peso para controlar la animación, etc (a veces también llamado canales).

Representaciones

Las mallas poligonales se pueden representar de diversas formas, utilizando diferentes métodos para almacenar los datos de vértices, aristas y caras. Éstas incluyen:

Meshes Face-vertex

Una simple lista de vértices, y un conjunto de polígonos que apuntan a los vértices que utiliza.

Ganada.

en el que cada borde apunta a dos vértices, dos caras, y los cuatro (a la derecha y en sentido contrario) bordes que los tocan. Las mallas de forja ganada permiten una constante traversión de tiempo de la superficie, pero con mayores requisitos de almacenamiento.

Meshes de media planta

Similar a las mallas alas-edge excepto que sólo se utiliza la mitad de la información de traversal del borde. (ver OpenMesh)

Mallas de cuádruple

que almacenan bordes, medias plantas y vértices sin ninguna referencia a polígonos. Los polígonos son implícitos en la representación, y pueden encontrarse atravesando la estructura. Los requerimientos de memoria son similares a las mallas de media planta.

Mesas de esquina

que almacena vértices en una tabla predefinida, tal que atravesar la tabla define implícitamente polígonos. Esto es en esencia el fan del triángulo utilizado en la renderización de gráficos de hardware. La representación es más compacta y más eficiente para recuperar polígonos, pero las operaciones para cambiar polígonos son lentas. Además, las mesas de esquina no representan las mallas completamente. Se necesitan múltiples mesas de esquina (aficionados al triángulo) para representar la mayoría de mallas.

Meshes Vertex-vertex

A "VV"la malla representa sólo vértices, que apuntan a otros vértices. Tanto la información de borde y cara es implícita en la representación. Sin embargo, la simplicidad de la representación no permite realizar muchas operaciones eficientes en mallas.

Cada una de las representaciones anteriores tiene ventajas e inconvenientes particulares, que se analizan con más detalle en Smith (2006). La elección de la estructura de datos se rige por la aplicación, el rendimiento requerido, el tamaño de los datos y las operaciones a realizar. Por ejemplo, es más fácil trabajar con triángulos que con polígonos generales, especialmente en geometría computacional. Para determinadas operaciones es necesario tener un acceso rápido a información topológica como aristas o caras vecinas; esto requiere estructuras más complejas, como la representación del borde alado. Para el renderizado de hardware, se necesitan estructuras compactas y simples; por lo tanto, la tabla de esquina (ventilador triangular) se incorpora comúnmente en API de renderizado de bajo nivel como DirectX y OpenGL.

Mallas vértice-vértice

Las

mallas vértice-vértice representan un objeto como un conjunto de vértices conectados a otros vértices. Esta es la representación más simple, pero no se usa mucho ya que la información de cara y borde está implícita. Por lo tanto, es necesario recorrer los datos para generar una lista de caras para renderizar. Además, las operaciones en aristas y caras no se realizan fácilmente.

Sin embargo, las mallas VV se benefician del pequeño espacio de almacenamiento y de una transformación eficiente de la forma. La figura anterior muestra una caja de cuatro lados representada por una malla VV. Cada vértice indexa sus vértices vecinos. Los dos últimos vértices, 8 y 9 en el centro superior e inferior del "cilindro de caja", tienen cuatro vértices conectados en lugar de cinco. Un sistema general debe poder manejar un número arbitrario de vértices conectados a cualquier vértice determinado.

Para obtener una descripción completa de las mallas VV, consulte Smith (2006).

Mallas cara-vértice

Las

mallas cara-vértice representan un objeto como un conjunto de caras y un conjunto de vértices. Esta es la representación de malla más utilizada y es la entrada que suele aceptar el hardware de gráficos moderno.

Las mallas cara-vértice mejoran las mallas VV para modelado porque permiten la búsqueda explícita de los vértices de una cara y de las caras que rodean un vértice. La figura anterior muestra el "cilindro de caja" ejemplo como una malla FV. Vertex v5 está resaltado para mostrar las caras que lo rodean. Observe que, en este ejemplo, se requiere que cada cara tenga exactamente 3 vértices. Sin embargo, esto no significa que cada vértice tenga el mismo número de caras circundantes.

Para renderizar, la lista de caras generalmente se transmite a la GPU como un conjunto de índices de vértices, y los vértices se envían como estructuras de posición/color/normal (en la figura, solo se proporciona la posición). Esto tiene la ventaja de que los cambios de forma, pero no de geometría, se pueden actualizar dinámicamente simplemente reenviando los datos del vértice sin actualizar la conectividad de la cara.

El modelado requiere un fácil recorrido de todas las estructuras. Con mallas cara-vértice es fácil encontrar los vértices de una cara. Además, la lista de vértices contiene una lista de caras conectadas a cada vértice. A diferencia de las mallas VV, tanto las caras como los vértices son explícitos, por lo que localizar caras y vértices vecinos es un tiempo constante. Sin embargo, las aristas están implícitas, por lo que aún es necesaria una búsqueda para encontrar todas las caras que rodean una cara determinada. Otras operaciones dinámicas, como dividir o fusionar una cara, también resultan difíciles con las mallas cara-vértice.

Mallas con borde alado

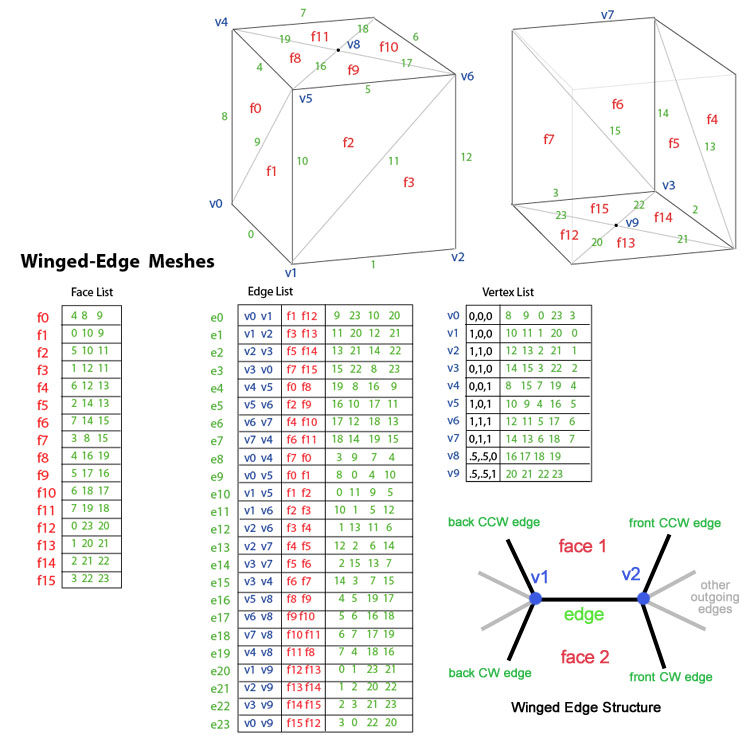
Figure 4. Winged-edge meshes — Gráfico 4. Manchas de filo ganado

Introducidas por Baumgart en 1975, las mallas de bordes alados representan explícitamente los vértices, caras y bordes de una malla. Esta representación se usa ampliamente en programas de modelado para proporcionar la mayor flexibilidad al cambiar dinámicamente la geometría de la malla, porque las operaciones de división y fusión se pueden realizar rápidamente. Su principal inconveniente son los grandes requisitos de almacenamiento y la mayor complejidad debido al mantenimiento de muchos índices. Se puede encontrar una buena discusión sobre los problemas de implementación de las mallas de borde alado en el libro Graphics Gems II.

Las mallas de bordes alados abordan el problema de atravesar de un borde a otro y proporcionar un conjunto ordenado de caras alrededor de un borde. Para cualquier arista dada, el número de aristas salientes puede ser arbitrario. Para simplificar esto, las mallas con bordes alados proporcionan solo cuatro, los bordes más cercanos en el sentido de las agujas del reloj y en el sentido contrario a las agujas del reloj en cada extremo. Los otros bordes se pueden recorrer de forma incremental. Por lo tanto, la información de cada borde se asemeja a una mariposa, de ahí el término "borde alado". mallas. La figura anterior muestra el "cilindro de caja" como una malla de borde alado. Los datos totales de una arista constan de 2 vértices (puntos finales), 2 caras (en cada lado) y 4 aristas (arista alada).

La renderización de mallas con bordes alados para hardware de gráficos requiere generar una lista de índice de caras. Por lo general, esto se hace solo cuando cambia la geometría. Las mallas de bordes alados son ideales para geometría dinámica, como superficies de subdivisión y modelado interactivo, ya que los cambios en la malla pueden ocurrir localmente. El recorrido a través de la malla, como podría ser necesario para la detección de colisiones, se puede lograr de manera eficiente.

Ver Baumgart (1975) para más detalles.

Renderizar mallas dinámicas

Las mallas de bordes alados no son la única representación que permite cambios dinámicos en la geometría. Una nueva representación que combina mallas de bordes alados y mallas de cara-vértice es la malla dinámica de renderizado, que almacena explícitamente tanto los vértices de una cara como las caras de un vértice (como las mallas FV), y la caras y vértices de una arista (como arista alada).

El renderizado de mallas dinámicas requiere un poco menos de espacio de almacenamiento que las mallas estándar con bordes alados y se pueden renderizar directamente mediante hardware de gráficos, ya que la lista de caras contiene un índice de vértices. Además, el recorrido de vértice a cara es explícito (tiempo constante), al igual que de cara a vértice. Las mallas RD no requieren los cuatro bordes salientes, ya que estos se pueden encontrar atravesando de borde a cara y luego de cara a borde vecino.

Las mallas RD se benefician de las características de las mallas de borde alado al permitir que la geometría se actualice dinámicamente.

Ver Tobler & Maierhofer (WSCG 2006) para más detalles.

Resumen de representación de malla

Operación		Vertex-vertex	Face-vertex	Ganada.	Dinámica de carga
V-V	Todos los vértices alrededor del vértice	Explicit	V → f1, f2, f3,... → v1, v2, v3,...	V → e1, e2, e3,... → v1, v2, v3,...	V → e1, e2, e3,... → v1, v2, v3,...
E-F	Todos los bordes de una cara	F(a,b,c) → {a,b}, {b,c}, {a,c}	F → {a,b}, {b,c}, {a,c}	Explicit	Explicit
V-F	Todos los vértices de una cara	F(a,b,c) → {a,b,c}	Explicit	F → e1, e2, e3 → a, b, c	Explicit
F-V	Todas las caras alrededor de un vértice	Búsqueda de pareja	Explicit	V → e1, e2, e3 → f1, f2, f3,...	Explicit
E-V	Todos los bordes alrededor de un vértice	V → {v,v1}, {v,v2}, {v,v3},...	V → f1, f2, f3,... → v1, v2, v3,...	Explicit	Explicit
F-E	Ambas caras de un borde	Comparación de listas	Comparación de listas	Explicit	Explicit
V-E	Ambos vértices de un borde	E(a,b) → {a,b}	E(a,b) → {a,b}	Explicit	Explicit
Flook	Encontrar cara con vértices dados	F(a,b,c) → {a,b,c}	Establecer intersección de v1,v2,v3	Establecer intersección de v1,v2,v3	Establecer intersección de v1,v2,v3
Tamaño del almacenamiento		V*avg(V,V)	3F + V*avg(F,V)	3F + 8E + V*avg(E,V)	6F + 4E + V*avg(E,V)
		Ejemplo con 10 vértices, 16 caras, 24 bordes:
		10 * 5 = 50	316 + 105 = 98	316 + 824 + 10*5 = 290	616 + 424 + 10*5 = 242
Figure 6: summary of mesh representation operations

En la tabla anterior, explícito indica que la operación se puede realizar en tiempo constante, ya que los datos se almacenan directamente; list compare indica que se debe realizar una comparación de listas entre dos listas para realizar la operación; y búsqueda por pares indica que se debe realizar una búsqueda en dos índices. La notación avg(V,V) significa el número promedio de vértices conectados a un vértice dado; avg(E,V) significa el número promedio de aristas conectadas a un vértice dado, y avg(F,V) es el número promedio de caras conectadas a un vértice dado.

La notación "V → f1, f2, f3,... → v1, v2, v3,..." describe que se requiere un recorrido a través de múltiples elementos para realizar la operación. Por ejemplo, para obtener "todos los vértices alrededor de un vértice V determinado" Usando la malla cara-vértice, primero es necesario encontrar las caras alrededor del vértice V dado usando la lista de vértices. Luego, a partir de esas caras, usa la lista de caras para encontrar los vértices a su alrededor. Las mallas de borde alado almacenan explícitamente casi toda la información, y otras operaciones siempre atraviesan primero el borde para obtener información adicional. Las mallas vértice-vértice son la única representación que almacena explícitamente los vértices vecinos de un vértice determinado.

A medida que las representaciones de la malla se vuelven más complejas (de izquierda a derecha en el resumen), aumenta la cantidad de información almacenada explícitamente. Esto proporciona un acceso más directo y constante en tiempo al recorrido y la topología de varios elementos, pero a costa de una mayor sobrecarga y espacio para mantener los índices correctamente.

La Figura 7 muestra la información de conectividad para cada una de las cuatro técnicas descritas en este artículo. También existen otras representaciones, como mesas de medio borde y de esquina. Todas estas son variantes de cómo los vértices, las caras y las aristas se indexan entre sí.

Como regla general, las mallas de cara-vértice se utilizan siempre que un objeto debe representarse en hardware de gráficos que no cambia la geometría (conectividad), pero puede deformarse o transformarse (posiciones de vértice), como la representación en tiempo real de imágenes estáticas. o transformar objetos. Las mallas dinámicas de renderizado o de borde alado se utilizan cuando la geometría cambia, como en paquetes de modelado interactivos o para calcular superficies de subdivisión. Las mallas vértice-vértice son ideales para cambios eficientes y complejos en geometría o topología, siempre que la representación del hardware no sea un problema.

Otras representaciones

Racionalización de las mallas

guardar caras en una forma ordenada, pero independiente, para que la malla pueda ser transmitida en pedazos. El orden de las caras puede ser espacial, espectral o basado en otras propiedades de la malla. Las mallas de transmisión permiten una malla muy grande para ser renderizada incluso mientras se está cargando.

Mallas progresivas

transmitir el vértice y los datos faciales con niveles crecientes de detalle. Diferente streaming de mallas, mallas progresivas dan la forma general de todo el objeto, pero a bajo nivel de detalle. Datos adicionales, nuevos bordes y caras, aumentan progresivamente el detalle de la malla.

Mallas normales

transmitir cambios progresivos a una malla como un conjunto de desplazamientos normales de una malla base. Con esta técnica, una serie de texturas representan las modificaciones incrementales deseadas. Las mallas normales son compactas, ya que sólo se necesita un único valor escalar para expresar el desplazamiento. Sin embargo, la técnica requiere una compleja serie de transformaciones para crear las texturas de desplazamiento.

Formatos de archivo

Existen muchos formatos de archivo diferentes para almacenar datos de malla poligonal. Cada formato es más eficaz cuando se utiliza para el propósito previsto por su creador. Algunos de estos formatos se presentan a continuación:

Sufijo de archivo	Nombre de formato	Organization(s)	Programas	Descripción
.raw	Malla cruda	Desconocido	Varios	Abrir, solo formato ASCII. Cada línea contiene 3 vértices, separados por espacios, para formar un triángulo, así: X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3
.blend	Formato de archivo Blender	Blender Foundation	Blender 3D	Fuente abierta, formato binario solo
.fbx	Autodesk FBX Formato	Autodesk	Varios	Propietario. Existen especificaciones binarias y ASCII.
.3ds	3ds Max File	Autodesk	3ds Max	Un formato común pero anticuado con límites de 16 bits duros sobre el número de vértices y caras. Ni estandarizado ni bien documentado, pero solía ser un "estándar de facto" para el intercambio de datos.
.dae	Intercambio de activos digitales (COLLADA)	Sony Computer Entertainment, Khronos Group	N/A	Se apoya en "COLLAaburrido DEsign Acautiverio". Un formato universal diseñado para prevenir la incompatibilidad.
.dgn	MicroStation Archivo	Bentley Systems	MicroStation	Hay dos formatos de archivo dgn: pre-versión 8 y versión 8 (V8)
.3dm	Rhino File	Robert McNeel & Associates	Rhinoceros 3D
.dxf,	Formato de intercambio de dibujo	Autodesk	AutoCAD
.obj	Wavefront OBJ	Wavefront Technologies	Varios	Formato ASCII que describe la geometría 3D. Todos los vértices de las caras se ordenan en sentido contrario, haciendo implícitas las normales de la faceta. Las normales de la espuma se especifican por vértice.
.ply	Formato de archivo de poligon	Stanford University	Varios	Binary y ASCII
.pmd	Película poligonal Datos del fabricante	Yu Higuchi	MikuMikuDance	Formato de archivo binario apropiado para almacenar geometría modelo humanoide con información de riego, material y física.
.stl	Formato de estereolitografía	3D Systems	Muchos	Formato binario y ASCII diseñado originalmente para ayudar en CNC.
.amf	Fabricación aditiva Formato de archivo	ASTM International	N/A	Como el formato STL, pero con soporte nativo de color, material y constelación añadido.
.wrl	Virtual Reality Modeling Language	Web3D Consortium	Navegadores web	ISO Standard 14772-1:1997
.wrz	VRML Comprimido	Web3D Consortium	Navegadores web
.x3d,.x3db,.x3dv	Extensible 3D	Web3D Consortium	Navegadores web	Base XML, código abierto, libre de regalías, extensible e interoperable; también admite información de color, textura y escena. ISO Standard 19775/19776/19777
.x3dz,.x3dbz,.x3dvz	X3D Binario comprimido	Web3D Consortium	Navegadores web
.c4d	Cine 4D Archivo	Maxon	CINEMA 4D
.lwo	LightWave 3D objeto Archivo	NewTek	LightWave 3D
.smb	SCOREC apf	RPI SCOREC	PUMI	Meshes 3D adaptables de código abierto para flujos de trabajo de simulación basados en PDE.
.msh	Gmsh Mesh	GMsh Developers	GMsh Project	Fuente abierta, que proporciona una descripción de malla ASCII para elementos lineales y polinomiales interpolados en 1 a 3 dimensiones.
. mal	OGRE XML	OGRE Development Team	OGRE, purbásico	Fuente abierta. Formato binario (.mesh) y ASCII (.mesh.xml) disponible. Incluye datos para animación de vertex y animación de destino Morph (blendshape). Datos de animación esquelética en archivo separado (.skeleton).
.veg	Vega FEM tetraedral mesh	Jernej Barbič	Vega FEM	Fuente abierta. Almacena una malla tetraedral y sus propiedades materiales para la simulación FEM. ASCII (.veg) y formatos binarios (.vegb) disponibles.
.z3d	Z3d	Oleg Melashenko	Zanoza Modeler	-
.vtk	Malla VTK	VTK, Kitware	VTK, Paraview	Open, ASCII o formato binario que contiene muchos campos de datos diferentes, incluyendo datos de puntos, datos de células y datos de campo.
.l4d	Dibujo LAI4D	Laboratorio de Inteligencia Artificial para el Diseño	LAI4D	Formato de datos ASCII que describe un árbol jerárquico de entidades.

Contenido relacionado

Más resultados...