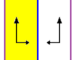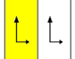Lista de grupos de simetría plana

Este artículo resume las clases de grupos de simetría discretos del plano euclidiano. Los grupos de simetría se nombran aquí mediante tres esquemas de nomenclatura: notación internacional, notación orbifold y notación de Coxeter. Hay tres tipos de grupos de simetría del plano:

• 2 familias de grupos de rosetas – 2D grupos de puntos
• 7 grupos frisos – Grupos de línea 2D
• 17 grupos de fondos de pantalla – 2D grupos espaciales.

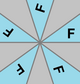
Grupos de rosetas

Hay dos familias de grupos de puntos bidimensionales discretos y se especifican con el parámetro n, que es el orden del grupo de rotaciones en el grupo.

Familia	Intl (orbifold)	Schön.	Geo Coxeter	Orden	Ejemplos
Simetría cíclica	n (n•)	Cn	n [n]+	n	C1, [ ]+ (•)	C2, [2]+ (2•)	C3[3]+ (3•)	C4[4]+ (4•)	C5, [5]+ (5•)	C6, [6]+ (6•)
Simetría Dihedral	nm (*n•)	Dn	n [n]	2n	D1[ ] (*•)	D2, [2] (*2•)	D3, [3] (*3•)	D4, [4] (*4•)	D5[5] (*5•)	D6, [6] (*6•)

Grupos de frisos

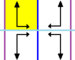
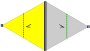
Los 7 grupos de frisos, los grupos de líneas bidimensionales, con una dirección de periodicidad, reciben cinco nombres de notación. La notación de Schönflies se da como límites infinitos de 7 grupos diédricos. Las regiones amarillas representan el dominio fundamental infinito en cada una.

[1, hígado], IUC (orbifold) Geo Schönflies Coxeter Fundamental dominio Ejemplo p1m1 (*∞•) p1 C∞v [1, hígado] silbido p1 (∞•) p1 CJUEGO [1, hígado]+ hop [2]+] IUC (orbifold) Geo Schönflies Coxeter Fundamental dominio Ejemplo p11m (∞*) p. 1 CLevántate [2]+] salto p11g (Firmado) p.g1 S2 mujeres [2]+, dieta+] paso

[2, hígado], IUC (orbifold) Geo Schönflies Coxeter Fundamental dominio Ejemplo p2mm (*22 Puestos) p2 DLevántate [2, hígado] salto giratorio p2mg (2*∞) p2g D∞d [2]+,∞] sillón giratorio p2 (22 hígados) p2 DJUEGO [2, hígado]+ spinning hop

Grupos de fondos de pantalla

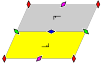
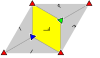
Los 17 grupos de papel tapiz, con dominios fundamentales finitos, están dados por notación internacional, notación orbifold y notación de Coxeter, clasificados por las 5 redes de Bravais en el plano: cuadrado, oblicuo (paralelogramático), hexagonal (triangular equilátero), rectangular (rómbico centrado) y rómbico (rectangular centrado).

Los grupos p1 y p2, sin simetría reflexiva, se repiten en todas las clases. El grupo de Coxeter reflexivo puro relacionado se proporciona con todas las clases excepto la oblicua.

Plaza [4,4], IUC (Orb.) Geo Coxeter Dominio Nombre de Conway p1 (°) p1 Monotropic p2 (2222) p2 [4,1]+4]+ [1]+,4,1+]+ Ditropic pgg (22×) pg2g [4]+,4+] Diglide pm (*22222) p2 [4,1]+4] [1]+,4,1+] Discópica cm (2*22) c2 [4.4.2]+) Dirhombic p4 (442) p4 [4,4]+ Tetratropic p4g (4*2) pg4 [4]+4] Tetragyro p4m (*442) p4 [4,4] Tetrascopio

Rectangular [Firmado]h,2, Vivirv] IUC (Orb.) Geo Coxeter Dominio Nombre de Conway p1 (°) p1 [Firmado]+,2, Vivir+] Monotropic p2 (2222) p2 [viejo,2, hígado]+ Ditropic pg(h) (××) pg1 h:+,(2, Vivir)+] Monoglide pg(v) (××) pg1 v: [(∞,2)+, dieta+] Monoglide pgm (22*) pg2 h:+,∞] Digyro pmg (22*) pg2 v: [Libertad,(2, hígado)+] Digyro h) (**) p1 h:+,2, hígado] Monoscopio pm(v) (**) p1 v: [puestos, 2, propuestos+] Monoscopio pm (*22222) p2 [viejo,2, hígado] Discópica

Rhombic [Firmado]h2+, dietav] IUC (Orb.) Geo Coxeter Dominio Nombre de Conway p1 (°) p1 [Firmado]+2+, dieta+] Monotropic p2 (2222) p2 [∞,2]+,∞]+ Ditropic cm(h) (*×) c1 h:+2+,∞] Monorhombic cm(v) (*×) c1 v: [∞,2]+, dieta+] Monorhombic pgg (22×) pg2g [(∞,2)+)[2]] Diglide cm (2*22) c2 [∞,2]+,∞] Dirhombic Paralelograma (oblicua) p1 (°) p1 Monotropic p2 (2222) p2 Ditropic

Hexagonal/Triangular [6,3], [3][3]] IUC (Orb.) Geo Coxeter Dominio Nombre de Conway p1 (°) p1 Monotropic p2 (2222) p2 [6,3]Δ Ditropic cm (2*22) c2 [6,3]⅄ Dirhombic p3 (333) p3 [1]+,6,3+] [3][3]]+ Tritrópico p3m1 (*333) p3 [1]+,6,3] [3][3]] Triscópico p31m (3*3) h3 [6,3]+] Trigyro p6 (632) p6 [6,3]+ Hexatropic p6m (*632) p6 [6,3] Hexascopio

Relaciones con subgrupos de papel pintado