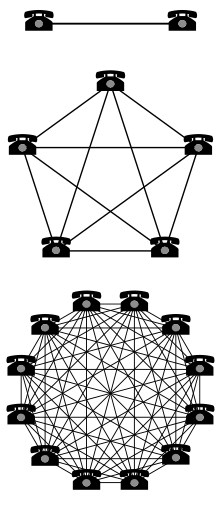
Ley de Metcalfe

Dos teléfonos pueden hacer sólo una conexión, cinco pueden hacer 10 conexiones, y doce pueden hacer 66 conexiones.

La ley de Metcalfe establece que el valor de una red de telecomunicaciones es proporcional al cuadrado del número de usuarios conectados del sistema (n²). Formulada por primera vez de esta forma por George Gilder en 1993, y atribuida a Robert Metcalfe con respecto a Ethernet, la ley de Metcalfe se presentó originalmente, c. 1980, no en términos de usuarios, sino de "dispositivos de comunicación compatibles" (por ejemplo, máquinas de fax, teléfonos). Solo más tarde, con la globalización de Internet, esta ley se trasladó a los usuarios y las redes, ya que su intención original era describir las conexiones Ethernet.

Efectos de red

La ley de Metcalfe caracteriza muchos de los efectos de la red de tecnologías y redes de comunicación como Internet, redes sociales y la World Wide Web. El ex Presidente de la Comisión Federal de Comunicaciones de EE.UU. Reed Hundt dijo que esta ley da la mayor comprensión a los trabajos de Internet. La Ley de Metcalfe está relacionada con el hecho de que el número de conexiones únicas posibles en una red de ${displaystyle n}$ nodos se pueden expresar matemáticamente como el número triangular ${displaystyle n(n-1)/2}$, que es asintóticamente proporcional a ${displaystyle n^{2}$.

La ley se ha ilustrado a menudo con el ejemplo de las máquinas de fax: una sola máquina de fax es inútil, pero el valor de cada máquina de fax aumenta con la cantidad total de máquinas de fax en la red, porque la cantidad total de personas con las que cada usuario podrá enviar y recibir documentos incrementa. Asimismo, en las redes sociales, cuanto mayor es el número de usuarios con el servicio, más valioso se vuelve el servicio para la comunidad.

Historia y derivación

La ley de Metcalfe fue concebida en 1983 en una presentación a la fuerza de ventas de 3Com. Declaró que V sería proporcional al número total de conexiones posibles, o aproximadamente n al cuadrado.

La encarnación original fue cuidadosa en delinear entre un costo lineal (Cn), un crecimiento no lineal, n², y un no -factor de proporcionalidad constante A “Afinidad”. El punto de equilibrio donde se recuperan los costos está dado por

${displaystyle Ctimes n=Atimes n(n-1)/2}$

En algún tamaño, el lado derecho de la ecuación V "Valor" excede el costo, y A describe la relación entre el tamaño y el valor agregado neto. Para n grandes, el valor neto de la red es entonces

${displaystyle Pi =n(Atimes (n-1)/2-C)}$

Metcalfe dimensionó correctamente A como "valor por usuario". La afinidad también es una función del tamaño de la red, y Metcalfe afirmó correctamente que A debe disminuir a medida que n crece. En una entrevista de 2006, Metcalfe declaró

Puede haber desaconomías de escala de red que eventualmente reducen los valores con un tamaño creciente. Entonces, si V=A*n², podría ser que A (para la “afinidad”, valor por conexión) es también una función de n y cabeza abajo después de un tamaño de red, abrumadora n².

Crecimiento de n

El tamaño de la red y, por lo tanto, el valor, no crece sin límites, sino que está limitado por limitaciones prácticas como la infraestructura, el acceso a la tecnología y la racionalidad limitada, como el número de Dunbar. Casi siempre ocurre que el crecimiento de usuarios n alcanza un punto de saturación. Con las tecnologías, los sustitutos, los competidores y la obsolescencia técnica limitan el crecimiento de n. Normalmente se supone que el crecimiento de n sigue una función sigmoidea, como una curva logística o una curva de Gompertz.

Densidad

A se rige también por la conectividad o densidad de la topología de la red. En una red no dirigida, cada borde conecta dos nodos tal que hay 2m nodos por borde. La proporción de nodos en contacto real se da por ${displaystyle c=2m/n}$.

El número máximo posible de bordes en una red simple (es decir, uno sin multi-edges o auto-edges) es ${displaystyle {binom} {n}{2}=n(n-1)/2}$. Por lo tanto la densidad *** de una red es la facción de los bordes que están realmente presentes es

${displaystyle rho =c/(n-1)}$que para las redes grandes se aproxima ${displaystyle rho =c/n}$.

Limitaciones

La ley de Metcalfe asume que el valor de cada nodo ${displaystyle n}$ es de igual beneficio. Si este no es el caso, por ejemplo porque una máquina de fax sirve a 60 trabajadores en una empresa, la segunda máquina de fax sirve la mitad de eso, el tercer tercio, y así sucesivamente, entonces el valor relativo de una conexión adicional disminuye. Asimismo, en las redes sociales, si los usuarios que se unen más tarde utilizan la red menos que los adoptadores tempranos, entonces el beneficio de cada usuario adicional puede disminuir, haciendo que la red global sea menos eficiente si los costos por usuario se fijan.

Modelos modificados

En el contexto de las redes sociales, muchos, incluido el propio Metcalfe, han propuesto modelos modificados en los que el valor de la red crece como ${displaystyle nlog n}$ en lugar de ${displaystyle n^{2}$. Reed y Andrew Odlyzko han buscado posibles relaciones con la Ley de Metcalfe en términos de describir la relación de una red y uno puede leer sobre cómo están relacionados. Tongia y Wilson también examinan la cuestión conexa de los costos para los excluidos.

Validación en datos

A pesar de muchos argumentos sobre la ley de Metcalfe, no hay evidencia real basada en datos para o contra estuvo disponible durante más de 30 años. Sólo en julio de 2013, investigadores holandeses lograron analizar patrones de uso de Internet europeos durante bastante tiempo y encontrados ${displaystyle n^{2}$ proporcionalidad para valores pequeños ${displaystyle n}$ y ${displaystyle nlog n}$ proporcionalidad para grandes valores ${displaystyle n}$. Unos meses más tarde, el propio Metcalfe proporcionó más pruebas, ya que utilizó los datos de Facebook en los últimos 10 años para mostrar un buen ajuste a la ley de Metcalfe (el modelo es ${displaystyle n^{2}$).

En 2015, Zhang, Liu y Xu parametrizaron la función Metcalfe en datos de Tencent y Facebook. Su trabajo demostró que la ley de Metcalfe se mantiene para ambos, a pesar de las diferencias de audiencia entre los dos sitios (Facebook que sirve a un público mundial y Tencent sólo sirve a los usuarios chinos). Las funciones de los dos sitios fueron ${displaystyle V_{Tencent}=7.39times 10^{-9}times n^{2}$ y ${displaystyle V_{Facebook}=5.70times 10^{-9}times n^{2}$ respectivamente.

En un documento de trabajo, Peterson vinculó los conceptos del valor del dinero en el tiempo con el valor de Metcalfe usando Bitcoin y Facebook como ejemplos numéricos de la prueba y en 2018 aplicó la ley de Metcalfe a Bitcoin, mostrando que más del 70 % de la variación en el valor de Bitcoin se explicó aplicando la ley de Metcalfe a los aumentos en el tamaño de la red de Bitcoin.