Lente lenticular

Una lente lenticular es un conjunto de lentes diseñadas para que, cuando se miran desde ángulos ligeramente diferentes, se muestren diferentes partes de la imagen que se encuentra debajo. El ejemplo más común son las lentes utilizadas en la impresión lenticular, donde la tecnología se utiliza para dar una ilusión de profundidad o para crear imágenes que parecen cambiar o moverse cuando se ve la imagen desde diferentes ángulos.

Aplicaciones

Impresión lenticular

La impresión lenticular es un proceso de varios pasos que consiste en crear una imagen lenticular a partir de al menos dos imágenes existentes y combinarla con una lente lenticular. Este proceso se puede utilizar para crear varios fotogramas de animación (para un efecto de movimiento), compensando las distintas capas en diferentes incrementos (para un efecto 3D) o simplemente para mostrar un conjunto de imágenes alternativas que pueden parecer transformarse entre sí.

Lentes correctoras

Las lentes lenticulares a veces se utilizan como lentes correctivas para mejorar la visión. Una lente bifocal podría considerarse un ejemplo sencillo.

Se han empleado lentes lenticulares para corregir la hipermetropía extrema (hipermetropía), una condición que a menudo se crea con la cirugía de cataratas cuando no es posible implantar lentes. Para limitar el gran grosor y peso que de otro modo requerirían lentes de alta potencia, toda la potencia de la lente se concentra en una pequeña área en el centro. En apariencia, una lente de este tipo a menudo se describe como parecida a un huevo frito: un hemisferio encima de una superficie plana. La superficie plana o "lente portador" tiene poca o ninguna potencia y está ahí simplemente para llenar el resto de la montura de las gafas y para sostener o "llevar" los lentes. la porción lenticular de la lente. Esta porción suele tener un diámetro de 40 mm (1,6 pulgadas), pero puede ser más pequeña, tan solo 20 mm (0,79 pulgadas), en potencias suficientemente altas. Estas lentes se utilizan generalmente para correcciones plus (hiperópicas) de aproximadamente 12 dioptrías o más. Un tipo similar de lente para anteojos es el miodisco, a veces denominado lente lenticular negativa, que se usa para correcciones negativas (miopes) muy altas. A veces se colocan diseños de lentes asféricos más estéticos. Se puede aplicar una película hecha de lentes cilíndricas moldeadas en un sustrato de plástico, como se muestra en la imagen de arriba, al interior de anteojos estándar para corregir la diplopía. La película normalmente se aplica al ojo con un buen control muscular de la dirección. La diplopía (también conocida como visión doble) generalmente es causada por una parálisis del sexto par craneal que impide el control total de los músculos que controlan la dirección hacia la que apunta el ojo. Estas películas se definen en la cantidad de grados de corrección que se necesitan donde cuanto mayor sea el grado, mayor será la corrección directiva que se necesita.

Pantallas lenticulares

Las pantallas con una superficie lenticular moldeada se utilizan frecuentemente con sistemas de televisión de proyección. En este caso, el propósito de las lentes es enfocar más luz en un haz horizontal y permitir que escape menos luz por encima y por debajo del plano del espectador. De esta forma se aumenta el brillo aparente de la imagen.

Las pantallas de proyección frontal comunes también pueden describirse como lenticulares. En este caso, en lugar de lentes transparentes, las formas formadas son pequeños reflectores curvos. Las pantallas lenticulares se utilizan con mayor frecuencia para pantallas de proyección que rechazan la luz ambiental para proyectores de alcance ultracorto. La estructura lenticular de la superficie refleja la luz del proyector al espectador sin reflejar la luz de las fuentes situadas encima de la pantalla.

Televisión 3D

A partir de 2010, varios fabricantes estaban desarrollando televisores 3D de alta definición autoestereoscópicos, utilizando sistemas de lentes lenticulares para evitar la necesidad de gafas especiales. Uno de ellos, el fabricante chino TCL, vendía un modelo LCD de 42 pulgadas (110 cm), el TD-42F, en China por unos 20.000 dólares.

En 2021, sólo los fabricantes especializados fabricarán este tipo de pantallas.

Procesos cinematográficos lenticulares en color

Las lentes lenticulares se utilizaron en los primeros procesos cinematográficos en color de la década de 1920, como el sistema Keller-Dorian y Kodacolor. Esto permitió obtener imágenes en color con el uso de películas meramente monocromáticas.

Ángulo de visión de una impresión lenticular

El ángulo de visión de una impresión lenticular es el rango de ángulos dentro del cual el observador puede ver la imagen completa. Esto está determinado por el ángulo máximo en el que un rayo puede salir de la imagen a través de la lentícula correcta.

Ángulo dentro de la lente

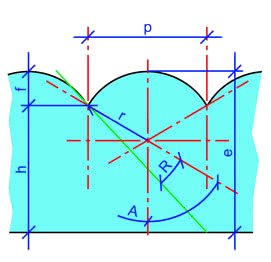
El diagrama de la derecha muestra en verde el rayo más extremo dentro de la lente lenticular que será refractado correctamente por la lente. Este rayo sale por un borde de una franja de imagen (en la parte inferior derecha) y sale por el borde opuesto de la lentícula correspondiente.

Definiciones

• R{displaystyle R. es el ángulo entre el rayo extremo y la normalidad en el punto donde sale la lente,
• p{displaystyle p} es el campo, o ancho de cada célula lenticular,
• r{displaystyle r} es el radio de curvatura de la cúpula,
• e{displaystyle e} es el espesor de la lente lenticular
• h{displaystyle h} es el espesor del sustrato debajo de la superficie curvada de la lente, y
• n{displaystyle n} es el índice de refracción de la lente.

Cálculo

R=A− − arctan⁡ ⁡ ()ph){displaystyle R=A-arctan left({pover h}right)},

dónde

A=arcsin⁡ ⁡ ()p2r){displaystyle A=arcsin left({p over 2r}right)},

h=e− − f{displaystyle h=e-f} es la distancia de la parte posterior de la grada al borde de la lenticule, y

f=r− − r2− − ()p2)2{displaystyle f=r-{sqrt {r^{2}-left({pover 2}right)}}}}.

Ángulo fuera de la lente

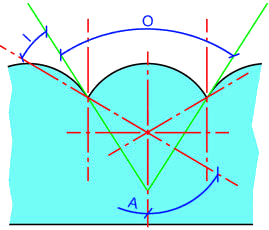
El ángulo fuera de la lente se da por refracción del rayo determinado arriba. El ángulo completo de la observación O{displaystyle O. es dado por

O=2()A− − I){displaystyle O=2(A-I)},

Donde I{displaystyle I} es el ángulo entre el rayo extremo y la normalidad afuera la lente. De la Ley de Snell,

I=arcsin⁡ ⁡ ()npecado⁡ ⁡ ()R)na){displaystyle I=arcsin left({nsin(R) over n_{a}right)},

Donde na. . 1.0003{displaystyle No. es el índice de refracción del aire.

Ejemplo

Considere una impresión lenticular que tiene lentes con 336.65 μm de campo, 190.5 μm de radio de curvatura, 457 μm de espesor, y un índice de refracción de 1.557. El ángulo completo de la observación O{displaystyle O. sería 64.6°.

Plano focal posterior de una red lenticular

La distancia focal de la lente se calcula a partir de la ecuación del fabricante de lentes, que en este caso se simplifica a:

F=rn− − 1{displaystyle F={r over n-1},

Donde F{displaystyle F} es la longitud focal de la lente.

El plano focal trasero se encuentra a una distancia BFD{displaystyle BFD} desde la parte posterior de la lente:

BFD=F− − en.{displaystyle BFD=F-{e over n}

Un BFD negativo indica que el plano focal se encuentra dentro de la lente.

En la mayoría de los casos, los lentes lenticulares están diseñados para que el plano focal posterior coincida con el plano posterior de la lente. La condición para esta coincidencia es BFD=0{displaystyle BFD=0}o

e=nrn− − 1.{displaystyle e={nr over n-1}

Esta ecuación impone una relación entre el espesor de la lente e{displaystyle e} y su radio de curvatura r{displaystyle r}.

Ejemplo

La lente lenticular en el ejemplo anterior tiene una distancia focal de 342 μm y una distancia focal trasera de 48 μm, lo que indica que el plano focal de la lente cae 48 micrómetros detrás de la imagen impresa en la parte posterior de la lente. .