Kappa de cohen

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Acuerdo estadístico de medición entre emisores para artículos categóricos

coeficiente kappa de Cohen (κ, kappa griego en minúsculas) es una estadística que se utiliza para medir la confiabilidad entre evaluadores. (y también la confiabilidad intraevaluador) para elementos cualitativos (categóricos). Generalmente se piensa que es una medida más sólida que el simple cálculo del acuerdo porcentual, ya que κ tiene en cuenta la posibilidad de que el acuerdo se produzca por casualidad. Existe controversia en torno al kappa de Cohen debido a la dificultad para interpretar los índices de concordancia. Algunos investigadores han sugerido que es conceptualmente más sencillo evaluar el desacuerdo entre ítems.

Historia

La primera mención de una estadística similar a kappa se atribuye a Galton en 1892.

El artículo fundamental que introdujo kappa como una nueva técnica fue publicado por Jacob Cohen en la revista Educational and Psychological Measurement en 1960.

Definición

Cohen's kappa mide el acuerdo entre dos tasadores que cada clasificación N ítems en C categorías mutuamente excluyentes. La definición de ${textstyle kappa }$ es

{displaystyle kappa equiv {frac {p_{o}-p_{e}}{1-p_{e}}}=1-{frac {1-p_{o}}{1-p_{e}}},}

Donde $p o$ es el acuerdo relativo observado entre los tasadores, y $p e$ es la probabilidad hipotética de acuerdo de oportunidad, utilizando los datos observados para calcular las probabilidades de cada observador al azar viendo cada categoría. Si los tasadores están en acuerdo completo entonces ${textstyle kappa =1}$ . Si no hay acuerdo entre los tasadores que no sea lo que se esperaría por casualidad (como se da por $p e$ ), ${textstyle kappa =0}$ . Es posible que la estadística sea negativa, que puede ocurrir por casualidad si no hay relación entre las calificaciones de los dos evaluadores, o puede reflejar una tendencia real de los tasadores a dar calificaciones diferentes.

Para $k$ categorías, $N$ observaciones para clasificar y clasificar ${displaystyle n_{ki}}$ el número de veces más $i$ Categoría prevista $k$ :

{displaystyle p_{e}={frac {1}{N^{2}}}sum _{k}n_{k1}n_{k2}}

Esto se deriva de la siguiente construcción:

{displaystyle p_{e}=sum _{k}{widehat {p_{k12}}}{overset {text{ind.}}{=}}sum _{k}{widehat {p_{k1}}}{widehat {p_{k2}}}=sum _{k}{frac {n_{k1}}{N}}{frac {n_{k2}}{N}}={frac {1}{N^{2}}}sum _{k}n_{k1}n_{k2}}

Donde ${displaystyle {widehat {p_{k12}}}}$ es la probabilidad estimada de que el valor 1 y el factor 2 clasificarán el mismo elemento que k, mientras que ${displaystyle {widehat {p_{k1}}}}$ es la probabilidad estimada que el factor 1 clasificará un elemento como k (y similarmente para el factor 2). La relación ${textstyle {widehat {p_{k}}}=sum _{k}{widehat {p_{k1}}}{widehat {p_{k2}}}}$ se basa en el uso de la suposición de que la calificación de los dos tasadores es independiente. El término ${displaystyle {widehat {p_{k1}}}}$ se calcula utilizando el número de artículos clasificados como k por rater 1 ( ${displaystyle n_{k1}}$ ) dividido por los elementos totales para clasificar ( ${displaystyle N}$ ): ${displaystyle {widehat {p_{k1}}}={n_{k1} over N}}$ (y similarmente para el rater 2).

Matriz de confusión de clasificación binaria

En la tradicional matriz de confusión 2 × 2 empleada en el aprendizaje automático y la estadística para evaluar clasificaciones binarias, la fórmula Kappa de Cohen se puede escribir como:

{displaystyle kappa ={frac {2times (TPtimes TN-FNtimes FP)}{(TP+FP)times (FP+TN)+(TP+FN)times (FN+TN)}}}

donde TP son los verdaderos positivos, FP son los falsos positivos, TN son los verdaderos negativos, y FN son los falsos negativos. En este caso, la Kappa de Cohen es equivalente a la Heidke puntuación de habilidad conocido en Meteorología. La medida fue introducida por primera vez por Myrick Haskell Doolittle en 1888.

Ejemplos

Ejemplo sencillo

Supongamos que está analizando datos relacionados con un grupo de 50 personas que solicitan una subvención. Cada propuesta de subvención fue leída por dos lectores y cada lector dijo "Sí" o "No" a la propuesta. Supongamos que los datos del recuento de desacuerdos fueran los siguientes, donde A y B son lectores, los datos en la diagonal principal de la matriz (a y d) cuentan el número de acuerdos y los datos fuera de la diagonal (byc) cuentan el número de desacuerdos:

B A	Sí.	No
Sí.	a	b
No	c	d

p.ej.

B A	Sí.	No
Sí.	20	5
No	10	15

El acuerdo proporcional observado es:

{displaystyle p_{o}={frac {a+d}{a+b+c+d}}={frac {20+15}{50}}=0.7}

Para calcular $p e$ (la probabilidad de acuerdo aleatorio) observamos que:

Reader A dijo "Sí" a 25 solicitantes y "No" a 25 solicitantes. Así el lector A dijo "Sí" 50% del tiempo.
El lector B dijo "Sí" a 30 solicitantes y "No" a 20 solicitantes. Así el lector B dijo "Sí" 60% del tiempo.

Entonces, la probabilidad esperada de que ambos digan que sí al azar es:

{displaystyle p_{text{Yes}}={frac {a+b}{a+b+c+d}}cdot {frac {a+c}{a+b+c+d}}=0.5times 0.6=0.3}

Del mismo modo:

{displaystyle p_{text{No}}={frac {c+d}{a+b+c+d}}cdot {frac {b+d}{a+b+c+d}}=0.5times 0.4=0.2}

La probabilidad general de acuerdo aleatorio es la probabilidad de que hayan acordado Sí o No, es decir:

{displaystyle p_{e}=p_{text{Yes}}+p_{text{No}}=0.3+0.2=0.5}

Así que ahora aplicando nuestra fórmula para la Kappa de Cohen obtenemos:

{displaystyle kappa ={frac {p_{o}-p_{e}}{1-p_{e}}}={frac {0.7-0.5}{1-0.5}}=0.4}

Mismos porcentajes pero diferentes números

Un caso que a veces se considera un problema con el Kappa de Cohen ocurre cuando se compara el Kappa calculado para dos pares de evaluadores con los dos evaluadores de cada par teniendo el mismo porcentaje de acuerdo pero un par da un número similar de calificaciones. en cada clase, mientras que el otro par da un número muy diferente de calificaciones en cada clase. (En los casos siguientes, la notificación B tiene 70 sí y 30 no, en el primer caso, pero esos números se invierten en el segundo). Por ejemplo, en los dos casos siguientes hay igual acuerdo entre A y B (60 de 100 en ambos casos) en términos de concordancia en cada clase, por lo que esperaríamos que los valores relativos de Kappa de Cohen reflejaran esto. Sin embargo, calculando el Kappa de Cohen para cada uno:

B A	Sí.	No
Sí.	45	15
No	25	15

{displaystyle kappa ={frac {0.60-0.54}{1-0.54}}=0.1304}

B A	Sí.	No
Sí.	25	35
No	5	35

{displaystyle kappa ={frac {0.60-0.46}{1-0.46}}=0.2593}

encontramos que muestra mayor similitud entre A y B en el segundo caso, en comparación con el primero. Esto se debe a que, si bien el acuerdo porcentual es el mismo, el acuerdo porcentual que se produciría "por casualidad" es diferente. es significativamente mayor en el primer caso (0,54 frente a 0,46).

Propiedades

Prueba de hipótesis e intervalo de confianza

Rara vez se informa el valor P para kappa, probablemente porque incluso valores relativamente bajos de kappa pueden ser significativamente diferentes de cero, pero no de magnitud suficiente para satisfacer a los investigadores. Aún así, su error estándar ha sido descrito. y se calcula mediante varios programas informáticos.

Se pueden construir intervalos de confianza para Kappa, para los valores de Kappa esperados si tuviéramos un número infinito de elementos verificados, usando la siguiente fórmula:

{displaystyle CI:kappa pm Z_{1-alpha /2}SE_{kappa }}

Donde ${displaystyle Z_{1-alpha /2}=1.960}$ es el percentil normal cuando ${displaystyle alpha =5%}$ , y ${displaystyle SE_{kappa }={sqrt {{p_{o}(1-p_{o})} over {N(1-p_{e})^{2}}}}}$

Esto se calcula ignorando que $p e$ se calcula a partir de los datos, y $p o$ como probabilidad estimada de una distribución binomial mientras utiliza la normalidad asintotica (es decir: suponiendo que el número de artículos es grande y que $p o$ no está cerca de 0 o 1). ${displaystyle SE_{kappa }}$ (y el CI en general) también se puede estimar utilizando métodos de arranque.

Interpretación de la magnitud

Si la significación estadística no es una guía útil, ¿qué magnitud de kappa refleja una concordancia adecuada? Sería útil disponer de directrices, pero otros factores además del acuerdo pueden influir en su magnitud, lo que hace que la interpretación de una magnitud determinada sea problemática. Como señalaron Sim y Wright, dos factores importantes son la prevalencia (son los códigos equiprobables o varían sus probabilidades) y el sesgo (son las probabilidades marginales para los dos observadores similares o diferentes). En igualdad de condiciones, los kappas son más altos cuando los códigos son equiprobables. Por otro lado, los Kappas son mayores cuando los códigos se distribuyen asimétricamente entre los dos observadores. A diferencia de las variaciones de probabilidad, el efecto del sesgo es mayor cuando Kappa es pequeño que cuando es grande.

Otro factor es el número de códigos. A medida que aumenta el número de códigos, los kappas aumentan. Basándose en un estudio de simulación, Bakeman y sus colegas concluyeron que para los observadores falibles, los valores de kappa eran más bajos cuando había menos códigos. Y, de acuerdo con Sim & Según la afirmación de Wright sobre la prevalencia, los kappas eran mayores cuando los códigos eran aproximadamente equiprobables. Así, Bakeman et al. concluyó que "ningún valor de kappa puede considerarse universalmente aceptable". También proporcionan un programa informático que permite a los usuarios calcular valores de kappa especificando el número de códigos, su probabilidad y la precisión del observador. Por ejemplo, dados códigos equiprobables y observadores con una precisión del 85%, el valor de kappa es 0,49, 0,60, 0,66 y 0,69 cuando el número de códigos es 2, 3, 5 y 10, respectivamente.

Sin embargo, en la literatura han aparecido pautas de magnitud. Quizás los primeros fueron Landis y Koch, quien caracterizó los valores < 0 indica que no hay acuerdo y 0-0,20 es leve, 0,21-0,40 es regular, 0,41-0,60 es moderado, 0,61-0,80 es sustancial y 0,81-1 es un acuerdo casi perfecto. Sin embargo, este conjunto de directrices no está en absoluto aceptado universalmente; Landis y Koch no aportaron pruebas que lo respaldaran, sino que se basaron en opiniones personales. Se ha observado que estas pautas pueden ser más perjudiciales que útiles. Las directrices igualmente arbitrarias de Fleiss caracterizan kappas superiores a 0,75 como excelentes, entre 0,40 y 0,75 como regulares o buenas y por debajo de 0,40 como deficientes.

Kappa máximo

Kappa asume su valor máximo teórico de 1 sólo cuando ambos observadores distribuyen códigos de la misma manera, es decir, cuando las sumas de filas y columnas correspondientes son idénticas. Cualquier cosa menos es un acuerdo menos que perfecto. Aún así, el valor máximo que kappa podría alcanzar dadas distribuciones desiguales ayuda a interpretar el valor de kappa realmente obtenido. La ecuación para el máximo κ es:

{displaystyle kappa _{max }={frac {P_{max }-P_{exp }}{1-P_{exp }}}}

Donde ${displaystyle P_{exp }=sum _{i=1}^{k}P_{i+}P_{+i}}$ , como siempre, ${displaystyle P_{max }=sum _{i=1}^{k}min(P_{i+},P_{+i})}$ ,

k = número de códigos, ${displaystyle P_{i+}}$ son las probabilidades de fila, y ${displaystyle P_{+i}}$ son las probabilidades de columna.

Limitaciones

Kappa es un índice que considera el acuerdo observado con respecto a un acuerdo base. Sin embargo, los investigadores deben considerar cuidadosamente si el acuerdo inicial de Kappa es relevante para la pregunta de investigación particular. La línea de base de Kappa se describe frecuentemente como el acuerdo debido al azar, lo cual es sólo parcialmente correcto. El acuerdo de referencia de Kappa es el acuerdo que se esperaría debido a la asignación aleatoria, dadas las cantidades especificadas por los totales marginales de la tabla de contingencia cuadrática. Por lo tanto, κ = 0 cuando la asignación observada es aparentemente aleatoria, independientemente del desacuerdo en la cantidad restringido por los totales marginales. Sin embargo, para muchas aplicaciones, los investigadores deberían estar más interesados en el desacuerdo cuantitativo en los totales marginales que en el desacuerdo en la asignación, como se describe en la información adicional en la diagonal de la tabla de contingencia cuadrada. Por lo tanto, para muchas aplicaciones, la línea base de Kappa distrae más que esclarecedora. Considere el siguiente ejemplo:

Comparación 1
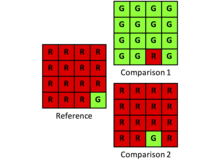
		Referencia
		G	R
Comparación	G	1	14
Comparación	R	0	1

La proporción de desacuerdo es 14/16 o 0,875. El desacuerdo se debe a la cantidad porque la asignación es óptima. κ es 0,01.

Comparación 2
		Referencia
		G	R
Comparación	G	0	1
Comparación	R	1	14

La proporción de desacuerdo es 2/16 o 0,125. El desacuerdo se debe a la asignación porque las cantidades son idénticas. Kappa es −0,07.

Aquí, informar el desacuerdo sobre la cantidad y la asignación es informativo, mientras que Kappa oscurece la información. Además, Kappa presenta algunos desafíos en el cálculo y la interpretación porque Kappa es una proporción. Es posible que la relación de Kappa devuelva un valor indefinido debido a cero en el denominador. Además, una razón no revela su numerador ni su denominador. Es más informativo para los investigadores informar desacuerdos en dos componentes: cantidad y asignación. Estos dos componentes describen la relación entre las categorías más claramente que una sola estadística resumida. Cuando el objetivo es la precisión predictiva, los investigadores pueden comenzar a pensar más fácilmente en formas de mejorar una predicción utilizando dos componentes de cantidad y asignación, en lugar de una proporción de Kappa.

Algunos investigadores han expresado preocupación por la tendencia de κ'a tomar las categorías observadas' frecuencias como dadas, lo que puede hacer que no sea confiable para medir la concordancia en situaciones como el diagnóstico de enfermedades raras. En estas situaciones, κ tiende a subestimar el acuerdo sobre la categoría rara. Por esta razón, κ se considera una medida de concordancia demasiado conservadora. Otros cuestionan la afirmación de que kappa "tiene en cuenta" acuerdo casual. Para hacer esto de manera efectiva se requeriría un modelo explícito de cómo el azar afecta las decisiones de los evaluadores. El llamado ajuste de probabilidad de las estadísticas kappa supone que, cuando no están completamente seguros, los evaluadores simplemente adivinan, un escenario muy poco realista. Además, algunos trabajos han demostrado cómo las estadísticas kappa pueden llevar a conclusiones erróneas en el caso de datos desequilibrados.

Estadísticas relacionadas

Pi de Scott

Scott (1955) propuso una estadística similar, llamada pi. La kappa de Cohen y la pi de Scott difieren en términos de cómo $p e$ es calculado.

Fleiss' kappa

Tenga en cuenta que el kappa de Cohen mide la concordancia entre dos evaluadores únicamente. Para una medida similar de acuerdo (kappa de Fleiss) utilizada cuando hay más de dos evaluadores, véase Fleiss (1971). Sin embargo, la kappa de Fleiss es una generalización de múltiples evaluadores del estadístico pi de Scott, no la kappa de Cohen. Kappa también se utiliza para comparar el rendimiento en el aprendizaje automático, pero se argumenta que la versión direccional conocida como Información o estadística J de Youden es más apropiada para el aprendizaje supervisado.

Kappa ponderado

El kappa ponderado permite ponderar los desacuerdos de manera diferente y es especialmente útil cuando se ordenan los códigos. Están involucradas tres matrices: la matriz de puntuaciones observadas, la matriz de puntuaciones esperadas basadas en el acuerdo aleatorio y la matriz de ponderación. Las celdas de la matriz de ponderación ubicadas en la diagonal (de arriba a la izquierda a abajo a la derecha) representan la concordancia y, por lo tanto, contienen ceros. Las celdas fuera de la diagonal contienen pesos que indican la gravedad de ese desacuerdo. A menudo, las celdas una de la diagonal tienen un peso de 1, las dos de 2, etc.

La ecuación para κ ponderada es:

{displaystyle kappa =1-{frac {sum _{i=1}^{k}sum _{j=1}^{k}w_{ij}x_{ij}}{sum _{i=1}^{k}sum _{j=1}^{k}w_{ij}m_{ij}}}}

Donde k= número de códigos y ${displaystyle w_{ij}}$ , ${displaystyle x_{ij}}$ , y ${displaystyle m_{ij}}$ son elementos en el peso, observado y matrices esperadas, respectivamente. Cuando las células diagonales contienen pesos de 0 y todos los pesos fuera de las células diagonales de 1, esta fórmula produce el mismo valor de kappa que el cálculo dado anteriormente.

Contenido relacionado

Más resultados...