Hiperrectángulo

En geometría, un hiperrectángulo (también llamado cuadro, hipercuadro u ortotopo), es el Generalización de un rectángulo (una figura plana) y del cuboide rectangular (una figura sólida) a dimensiones superiores. Una condición necesaria y suficiente es que sea congruente con el producto cartesiano de intervalos finitos. Si todas las aristas tienen la misma longitud, es un hipercubo. Un hiperrectángulo es un caso especial de paralelotopo.

Tipos

Un ortotopo de cuatro dimensiones es probablemente un hipercuboide.

El caso especial de un ortotopo n-dimensional donde todos los bordes tienen la misma longitud es el n-cubo o hipercubo.

Por analogía, el término "hiperrectángulo" puede referirse a productos cartesianos de intervalos ortogonales de otros tipos, como rangos de claves en teoría de bases de datos o rangos de números enteros, en lugar de números reales.

Politopo dual

El politopo dual de un ortotopo n se ha denominado de diversas formas n-orthoplex, rómbico n-fusil o n-lozenge. Está construido por 2n puntos ubicados en el centro de las caras rectangulares del ortotopo.

Un símbolo Schläfli de n-fusil se puede representar mediante una suma de n segmentos de línea ortogonales: { } + { } +... + { } o n{ }.

Un 1-fusil es un segmento de línea. Un 2-fusil es un rombo. Sus selecciones cruzadas planas en todos los pares de ejes son rombos.

n	Imagen de ejemplo
1	Serie de línea {}
2	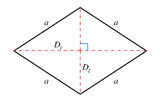Rhombus {fnK} 2{ }
3	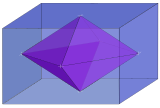Rhombic 3-orthoplex dentro 3-orthotope {} + {} + {} = 3{}