Hexaedro

Un hexaedro (plural: hexaedro) es cualquier poliedro de seis caras. Un cubo, por ejemplo, es un hexaedro regular con todas sus caras cuadradas y tres cuadrados alrededor de cada vértice.

Hay siete hexaedros convexos topológicamente distintos, uno de los cuales existe en dos formas de imagen especular. (Dos poliedros son 'topológicamente distintos' si tienen arreglos de caras y vértices intrínsecamente diferentes, de modo que es imposible distorsionar uno en el otro simplemente cambiando las longitudes de los bordes o los ángulos entre los bordes o las caras).

Cuboides

Hexaedro de caras cuadriláteras (cuboide) 6 caras, 12 aristas, 8 vértices
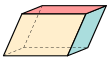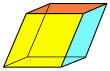Cubo (cuadrado)	Paralelepípedo rectangular (tres pares de rectángulos)	Trapezoedro trigonal (rombos congruentes)	Trapezoedro trigonal (cuadriláteros congruentes)	Frusto de cuadrilátero ( pirámide cuadrada truncada en el vértice )	Paralelepípedo (tres pares de paralelogramos)	Romboedro (tres pares de rombos)
Oh , [ 4,3 ], (*432) orden 48	D 2h , [2,2], (*222) orden 8	D 3 d , [2 ,6], (2*3) orden 12	D 3 , [2,3] , (223) orden 6	C 4v , [4], (*44) orden 8	C i , [2 ,2 ], (×) orden 2

Otros

Convexo
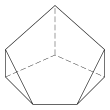Bipirámide triangular	Anticuña tetragonal. Quiral: existe en formas de imagen especular "zurdas" y "diestras".		Pirámide pentagonal
3 Caras 9 E, 5 V	4.4.3.3.3.3 Caras 10 E, 6 V	4.4.4.4.3.3 Caras 11 E, 7 V	5.3 Caras 10 E, 6 V	5.4.4.3.3.3 Caras 11 E, 7 V	5.5.4.4.3.3 Caras 12 E, 8 V

Hay otros tres hexaedros topológicamente distintos que solo se pueden realizar como figuras cóncavas :

Cóncavo
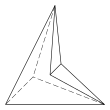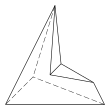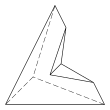4.4.3.3.3.3 Caras 10 E, 6 V	5.5.3.3.3.3 Caras 11 E, 7 V	6.6.3.3.3.3 Caras 12 E, 8 V

Un antiprisma digonal puede considerarse una forma degenerada de hexaedro, que tiene dos caras digonales opuestas y cuatro caras triangulares. Sin embargo, los digones generalmente no se tienen en cuenta en la definición de poliedros no esféricos, y este caso a menudo se considera simplemente un tetraedro y las cuatro caras triangulares restantes se consideran para componer el sólido completo.