Grupo heisenberg

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Grupo en teoría de grupos y física

En matemáticas, la Heisenberg group $H$ , nombrado por Werner Heisenberg, es el grupo de matrices triangulares superiores 3×3 de la forma

begin{pmatrix} 1 & a & c\ 0 & 1 & b\ 0 & 0 & 1\ end{pmatrix}

bajo la operación de multiplicación de matrices. Los elementos a, b y c se pueden tomar de cualquier anillo conmutativo con identidad, a menudo considerado como el anillo de números reales (lo que da como resultado el "grupo continuo de Heisenberg"). #34;) o el anillo de números enteros (lo que da como resultado el "grupo discreto de Heisenberg").

El grupo continuo de Heisenberg surge en la descripción de sistemas mecánicos cuánticos unidimensionales, especialmente en el contexto del teorema de Stone-von Neumann. De manera más general, se pueden considerar grupos de Heisenberg asociados a sistemas n-dimensionales y, más generalmente, a cualquier espacio vectorial simpléctico.

El caso tridimensional

En el caso tridimensional, el producto de dos matrices de Heisenberg viene dado por:

{displaystyle {begin{pmatrix}1&a&c\0&1&b\0&0&1\end{pmatrix}}{begin{pmatrix}1&a'&c'\0&1&b'\0&0&1\end{pmatrix}}={begin{pmatrix}1&a+a'&c+ab'+c'\0&1&b+b'\0&0&1\end{pmatrix}},.}

Showing translation for

As one can see from the term abn#39;, the group is non-abelian.

Did you mean:

The neutral element of the Heisenberg group is the identity matrix, and inverse are given by

begin{pmatrix} 1 & a & c\ 0 & 1 & b\ 0 & 0 & 1\ end{pmatrix}^{-1}= begin{pmatrix} 1 & -a & ab-c\ 0 & 1 & -b\ 0 & 0 & 1\ end{pmatrix},.

El grupo es un subgrupo del grupo Aff 2-dimensional (2): $begin{pmatrix} 1 & a & c\ 0 & 1 & b\ 0 & 0 & 1\ end{pmatrix}$ Actuando ${displaystyle ({vec {x}},1)}$ corresponde a la transformación de afine ${displaystyle {begin{pmatrix}1&a\0&1end{pmatrix}}{vec {x}}+{begin{pmatrix}c\bend{pmatrix}}}$ .

Hay varios ejemplos destacados del caso tridimensional.

Grupo continuo de Heisenberg

Did you mean:

If a, b, c, are real numbers (in the ring R) then one has the continuous Heisenberg group H₃(R).

Es un grupo de Lie real nilpotente de dimensión 3.

Además de la representación como matrices reales de 3×3, el grupo continuo de Heisenberg también tiene varias representaciones diferentes en términos de espacios funcionales. Según el teorema de Stone-von Neumann, existe, hasta el isomorfismo, una representación unitaria irreducible única de H en la que su centro actúa con un carácter no trivial dado. Esta representación tiene varias realizaciones o modelos importantes. En el modelo de Schrödinger, el grupo de Heisenberg actúa sobre el espacio de funciones cuadradas integrables. En la representación theta, actúa sobre el espacio de funciones holomorfas en el semiplano superior; Se llama así por su conexión con las funciones theta.

Grupo discreto de Heisenberg

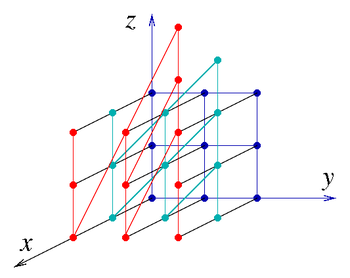
Una parte del gráfico Cayley del grupo discreto Heisenberg, con generadores *x,y,z* como en el texto. (La coloración es sólo para la ayuda visual.)

Si $a, b, c$ , son números enteros (en el anillo Z) entonces se tiene el grupo discreto de Heisenberg H₃(Z). Es un grupo nilpotente no abeliano. Tiene dos generadores,

x=begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 0\ 0 & 0 & 1\ end{pmatrix}, y=begin{pmatrix} 1 & 0 & 0\ 0 & 1 & 1\ 0 & 0 & 1\ end{pmatrix}

y relaciones

z^{}_{}=xyx^{-1}y^{-1}, xz=zx, yz=zy

dónde

z=begin{pmatrix} 1 & 0 & 1\ 0 & 1 & 0\ 0 & 0 & 1\ end{pmatrix}

es el generador del centro de H₃. (Tenga en cuenta que las inversas de x, y y z reemplazan el 1 sobre la diagonal con −1).

Did you mean:

By Bass 's theorem, it has a polynomial growth rate of order 4.

Se puede generar cualquier elemento a través de

begin{pmatrix} 1 & a & c\ 0 & 1 & b\ 0 & 0 & 1\ end{pmatrix}=y^bz^cx^a,.

Grupo de Heisenberg módulo un primo impar p

Si tomamos a, b, c en Z/p Z para un primo impar p, entonces tenemos el módulo del grupo de Heisenberg p. Es un grupo de orden p³ con generadores x,y y relaciones:

z^{}_{}=xyx^{-1}y^{-1}, x^p=y^p=z^p=1, xz=zx, yz=zy.

Los análogos de los grupos de Heisenberg sobre campos finitos de orden primo impar p se denominan grupos extra especiales, o más propiamente, grupos extra especiales de exponente p. De manera más general, si el subgrupo derivado de un grupo G está contenido en el centro Z de G, entonces el mapa de G/ Z × G/Z → Z es un operador bilineal simétrico sesgado en grupos abelianos.

Sin embargo, requerir que G/Z sea un espacio vectorial finito requiere que el subgrupo Frattini de G esté contenido en el centro, y requerir que Z sea un espacio vectorial unidimensional sobre Z/p Z requiere que Z tenga orden p, entonces si G no es abeliano, entonces G es extra especial. Si G es extra especial pero no tiene exponente p, entonces la construcción general siguiente aplicada al espacio vectorial simpléctico G/Z no produce un grupo isomorfo a G.

Grupo Heisenberg módulo 2

El grupo de Heisenberg módulo 2 es de orden 8 y es isomorfo al grupo diédrico D₄ (las simetrías de un cuadrado). Observa que si

x=begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 0\ 0 & 0 & 1\ end{pmatrix}, y=begin{pmatrix} 1 & 0 & 0\ 0 & 1 & 1\ 0 & 0 & 1\ end{pmatrix}

Entonces

xy=begin{pmatrix} 1 & 1 & 1\ 0 & 1 & 1\ 0 & 0 & 1\ end{pmatrix},

yx=begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1\ 0 & 0 & 1\ end{pmatrix}.

Los elementos x y y corresponden a reflexiones (con 45° entre ellos), mientras que xy y yx corresponden a rotaciones de 90°. Las otras reflexiones son xyx y yxy, y la rotación de 180° es xyxy (=yxyx).

Álgebra de Heisenberg

El álgebra de Lie ${mathfrak {h}}$ del grupo Heisenberg $H$ (sobre los números reales) se conoce como el álgebra Heisenberg. Puede ser representado usando el espacio de 3×3 matrices de la forma

{displaystyle {begin{pmatrix}0&a&c\0&0&b\0&0&0\end{pmatrix}},}

con ${displaystyle a,b,cin mathbb {R} }$ .

Los tres elementos siguientes constituyen una base para ${mathfrak {h}}$ ,

{displaystyle X={begin{pmatrix}0&1&0\0&0&0\0&0&0\end{pmatrix}};quad Y={begin{pmatrix}0&0&0\0&0&1\0&0&0\end{pmatrix}};quad Z={begin{pmatrix}0&0&1\0&0&0\0&0&0\end{pmatrix}}.}

Estos elementos básicos satisfacen las relaciones de conmutación,

{displaystyle [X,Y]=Z;quad [X,Z]=0;quad [Y,Z]=0}

Did you mean:

The name "Heisenberg group#34; is motivated by the preceding relations, which have the same form as the canonical commutation relations in quantum mechanics,

{displaystyle left[{hat {x}},{hat {p}}right]=ihbar I;quad left[{hat {x}},ihbar Iright]=0;quad left[{hat {p}},ihbar Iright]=0,}

Donde ${hat {x}}$ es el operador de posición, ${hat {p}}$ es el operador de impulso, y $hbar$ Es constante de Planck.

El grupo Heisenberg $H$ tiene la propiedad especial que el mapa exponencial es uno a uno y en el mapa del álgebra de Lie ${mathfrak {h}}$ al grupo $H$ ,

{displaystyle exp {begin{pmatrix}0&a&c\0&0&b\0&0&0\end{pmatrix}}={begin{pmatrix}1&a&c+{frac {ab}{2}}\0&1&b\0&0&1\end{pmatrix}}.}

En la teoría de campos conforme

En la teoría del campo conformado, el término álgebra Heisenberg se utiliza para referirse a una generalización infinita-dimensional del álgebra anterior. Es abarcado por elementos ${displaystyle a_{n},nin mathbb {Z} }$ , con relaciones de conmutación

{displaystyle [a_{n},a_{m}]=ndelta _{n+m,0}.}

Bajo un cambio de escala, esto es simplemente un número infinito y contable de copias del álgebra anterior.

Dimensiones superiores

Más general Grupos Heisenberg ${displaystyle H_{2n+1}}$ puede definirse para dimensiones superiores en el espacio euclidiano, y más generalmente en espacios vectoriales simpácticos. El caso general más simple es el verdadero grupo Heisenberg de dimensión $2n+1$ , para cualquier entero $ngeq 1$ . Como grupo de matrices, ${displaystyle H_{2n+1}}$ (o ${displaystyle H_{2n+1}(mathbb {R})}$ para indicar que este es el grupo Heisenberg sobre el terreno $mathbb {R}$ de números reales) se define como el grupo ${displaystyle (n+2)times (n+2)}$ matrices con entradas $mathbb {R}$ y tener la forma:

{displaystyle {begin{bmatrix}1&mathbf {a} &c\mathbf {0} &I_{n}&mathbf {b} \0&mathbf {0} &1end{bmatrix}}}

dónde

a es un vector de fila de longitud n,

b es un vector de columna de longitud n,

I_n es la matriz de identidad del tamaño n.

Estructura del grupo

Esto sí que es un grupo, como lo muestra la multiplicación:

begin{bmatrix} 1 & mathbf a & c \ 0 & I_n & mathbf b \ 0 & 0 & 1 end{bmatrix} cdot begin{bmatrix}1 & mathbf a' & c' \ 0 & I_n & mathbf b' \ 0 & 0 & 1 end{bmatrix} = begin{bmatrix} 1 & mathbf a+ mathbf a' & c+c' +mathbf a cdot mathbf b' \ 0 & I_n & mathbf b+mathbf b' \ 0 & 0 & 1 end{bmatrix}

begin{bmatrix} 1 & mathbf a & c \ 0 & I_n & mathbf b \ 0 & 0 & 1 end{bmatrix} cdot begin{bmatrix}1 & -mathbf a & -c +mathbf a cdot mathbf b\ 0 & I_n & -mathbf b \ 0 & 0 & 1 end{bmatrix} = begin{bmatrix} 1 & 0 & 0 \ 0 & I_n & 0 \ 0 & 0 & 1 end{bmatrix}.

Álgebra de mentiras

El grupo de Heisenberg es un grupo de Lie simplemente conexo cuyo álgebra de Lie consta de matrices

begin{bmatrix} 0 & mathbf a & c \ 0 & 0_n & mathbf b \ 0 & 0 & 0 end{bmatrix},

dónde

a es un vector de fila de longitud n,

b es un vector de columna de longitud n,

0_n es la matriz cero del tamaño n.

Al permitir que e₁,..., e_n sea la base canónica de Rⁿ y configuración

{displaystyle {begin{aligned}p_{i}&={begin{bmatrix}0&operatorname {e} _{i}^{mathrm {T} }&0\0&0_{n}&0\0&0&0end{bmatrix}},\q_{j}&={begin{bmatrix}0&0&0\0&0_{n}&operatorname {e} _{j}\0&0&0end{bmatrix}},\z&={begin{bmatrix}0&0&1\0&0_{n}&0\0&0&0end{bmatrix}},end{aligned}}}

el álgebra de Lie asociada se puede caracterizar por las relaciones de conmutación canónicas,

{begin{bmatrix}p_{i},q_{j}end{bmatrix}}=delta _{{ij}}z,qquad {begin{bmatrix}p_{i},zend{bmatrix}}=0,qquad {begin{bmatrix}q_{j},zend{bmatrix}}=0~,

donde p₁,..., p_n, q₁,..., q_n, z son los generadores de álgebra.

En particular, z es un elemento central del álgebra de Lie de Heisenberg. Tenga en cuenta que el álgebra de Lie del grupo de Heisenberg es nilpotente.

Mapa exponencial

Dejar

{displaystyle u={begin{bmatrix}0&mathbf {a} &c\0&0_{n}&mathbf {b} \0&0&0end{bmatrix}},}

que cumple ${displaystyle u^{3}=0_{n+2}}$ . El mapa exponencial evalúa a

{displaystyle exp(u)=sum _{k=0}^{infty }{frac {1}{k!}}u^{k}=I_{n+2}+u+{tfrac {1}{2}}u^{2}={begin{bmatrix}1&mathbf {a} &c+{1 over 2}mathbf {a} cdot mathbf {b} \0&I_{n}&mathbf {b} \0&0&1end{bmatrix}}.}

El mapa exponencial de cualquier álgebra de Lie nilpotente es un difeomorfismo entre el álgebra de Lie y el único grupo de Lie asociado, conectado y simplemente conectado.

Esta discusión (aparte de las declaraciones que se refieren a la dimensión y al grupo de Lie) se aplica aún más si reemplazamos R por cualquier anillo conmutativo A. El grupo correspondiente se denota H_n(A).

Bajo el supuesto adicional de que el primo 2 es invertible en el anillo A, el mapa exponencial también está definido, ya que se reduce a una suma finita y tiene la forma anterior (por ejemplo, A podría ser un anillo Z/p Z con un primo impar p o cualquier campo de característica 0).

Teoría de la representación

La teoría de la representación unitaria del grupo de Heisenberg es bastante simple (posteriormente generalizada por la teoría de Mackey) y fue la motivación para su introducción en la física cuántica, como se analiza a continuación.

Para cada número real no cero $hbar$ , podemos definir una representación unitaria irreducible ${displaystyle Pi _{hbar }}$ de ${displaystyle H_{2n+1}}$ actuando en el espacio Hilbert $L^2(mathbb R^n)$ por la fórmula:

{displaystyle left[Pi _{hbar }{begin{pmatrix}1&mathbf {a} &c\0&I_{n}&mathbf {b} \0&0&1end{pmatrix}}psi right](x)=e^{ihbar c}e^{ibcdot x}psi (x+hbar a)}

Esta representación se conoce como la representación Schrödinger. La motivación para esta representación es la acción de los operadores de posición y impulso exponentes en la mecánica cuántica. El parámetro $a$ describe las traducciones en espacio de posición, el parámetro $b$ describe las traducciones en el espacio de impulso, y el parámetro $c$ da un factor de fase general. El factor de fase es necesario para obtener un grupo de operadores, ya que las traducciones en el espacio de posición y las traducciones en el espacio de impulso no se comunican.

El resultado clave es el teorema Stone-von Neumann, que afirma que cada representación unitaria irreducible (fuertemente continua) del grupo Heisenberg en el que el centro actúa no triplicadamente equivale a ${displaystyle Pi _{hbar }}$ para algunos $hbar$ . Alternativamente, que todos son equivalentes al álgebra de Weyl (o álgebra de CCR) en un espacio simpléctico de la dimensión 2n.

Puesto que el grupo Heisenberg es una extensión central unidimensional $mathbb {R} ^{2n}$ , sus representaciones unitarias irreducibles pueden considerarse como representaciones proyectivas unitarias irreducibles de $mathbb {R} ^{2n}$ . Conceptualmente, la representación dada arriba constituye la contraparte mecánica cuántica al grupo de simetrías traduccionales en el espacio de fase clásica, $mathbb {R} ^{2n}$ . El hecho de que la versión cuántica sea sólo una proyecto representación de $mathbb {R} ^{2n}$ se sugiere ya a nivel clásico. Los generadores Hamiltonianos de traducciones en espacio de fase son las funciones de posición e impulso. El lazo de estas funciones no forman un álgebra de Lie bajo el soporte de Poisson, sin embargo, porque ${displaystyle {x_{i},p_{j}}=delta _{i,j}.}$ Más bien, el alcance de las funciones de posición e impulso y las constantes forma un álgebra Lie bajo el soporte Poisson. Este álgebra Lie es una extensión central unidimensional del álgebra de Lie conmutativa $mathbb {R} ^{2n}$ , isomorfo al álgebra de Lie del grupo Heisenberg.

Sobre espacios vectoriales simplécticos

La abstracción general de un grupo de Heisenberg se construye a partir de cualquier espacio vectorial simpléctico. Por ejemplo, sea (V, ω) un espacio vectorial simpléctico real de dimensión finita (por lo que ω es una forma bilineal simétrica sesgada no degenerada en V). El grupo de Heisenberg H(V) en (V, ω) (o simplemente V para abreviar) es el conjunto V×R dotado de la ley de grupo

{displaystyle (v,t)cdot left(v',t'right)=left(v+v',t+t'+{frac {1}{2}}omega left(v,v'right)right).}

El grupo de Heisenberg es una extensión central del grupo aditivo V. Por lo tanto hay una secuencia exacta

{displaystyle 0to mathbf {R} to H(V)to Vto 0.}

Cualquier espacio vectorial simpléctico admite una base de Darboux {e_j, f^k}_{1 ≤ j,k ≤ n} que satisface ω(e_j, f^k) = δ_j^k y donde 2n es la dimensión de V (la dimensión de V es necesariamente par). En términos de esta base, cada vector se descompone como

{displaystyle v=q^{a}mathbf {e} _{a}+p_{a}mathbf {f} ^{a}.}

La q^a y la p_a son coordenadas canónicamente conjugadas.

Si {e_j, f^k}_{1 ≤ j,k ≤ n} es una base de Darboux para V, entonces sea {E} una base para R y {e_j, f^k, E}_{1 ≤ j, k ≤ n} es la base correspondiente para V×R. Un vector en H(V) viene dado por

{displaystyle v=q^{a}mathbf {e} _{a}+p_{a}mathbf {f} ^{a}+tE}

y la ley de grupo se convierte en

{displaystyle (p,q,t)cdot left(p',q',t'right)=left(p+p',q+q',t+t'+{frac {1}{2}}(pq'-p'q)right).}

Debido a que la variedad subyacente del grupo de Heisenberg es un espacio lineal, los vectores en el álgebra de Lie pueden identificarse canónicamente con los vectores del grupo. El álgebra de Lie del grupo de Heisenberg viene dada por la relación de conmutación

{displaystyle {begin{bmatrix}(v_{1},t_{1}),(v_{2},t_{2})end{bmatrix}}=omega (v_{1},v_{2})}

o escrito en términos de la base Darboux

{displaystyle left[mathbf {e} _{a},mathbf {f} ^{b}right]=delta _{a}^{b}}

y todos los demás conmutadores desaparecen.

También es posible definir la ley de grupos de una manera diferente pero que produce un grupo isomorfo al grupo que acabamos de definir. Para evitar confusiones, usaremos u en lugar de t, por lo que un vector viene dado por

{displaystyle v=q^{a}mathbf {e} _{a}+p_{a}mathbf {f} ^{a}+uE}

y la ley de grupo es

{displaystyle (p,q,u)cdot left(p',q',u'right)=left(p+p',q+q',u+u'+pq'right).}

Un elemento del grupo

{displaystyle v=q^{a}mathbf {e} _{a}+p_{a}mathbf {f} ^{a}+uE}

puede entonces expresarse como una matriz

{displaystyle {begin{bmatrix}1&p&u\0&I_{n}&q\0&0&1end{bmatrix}}}

que da una representación matriz fiel de H(V). El u en esta formulación se relaciona con t en nuestra formulación anterior por ${displaystyle u=t+{tfrac {1}{2}}pq}$ Así que t valor para el producto viene a

{displaystyle {begin{aligned}&u+u'+pq'-{frac {1}{2}}left(p+p'right)left(q+q'right)\={}&t+{frac {1}{2}}pq+t'+{frac {1}{2}}p'q'+pq'-{frac {1}{2}}left(p+p'right)left(q+q'right)\={}&t+t'+{frac {1}{2}}left(pq'-p'qright)end{aligned}}}

como antes.

El isomorfismo del grupo que utiliza matrices triangulares superiores se basa en la descomposición de V en una base de Darboux, lo que equivale a una elección de isomorfismo V ≅ U ⊕ U*. Aunque la nueva ley de grupo produce un grupo isomorfo al grupo dado anteriormente, el grupo con esta ley a veces se denomina grupo de Heisenberg polarizado como recordatorio de que esta ley de grupo se basa en una elección de base. (una elección de un subespacio lagrangiano de V es una polarización).

Para cualquier álgebra de Lie, existe un grupo de Lie único, conectado y simplemente conectado G. Todos los demás grupos de Lie conectados con la misma álgebra de Lie que G tienen la forma G/N donde N es un grupo discreto central en G. En este caso, el centro de H(V) es R y los únicos subgrupos discretos son isomorfos a Z. Por tanto, H(V)/Z es otro grupo de Lie que comparte este álgebra de Lie. Es de destacar que este grupo de Lie no admite representaciones fieles de dimensión finita; no es isomorfo a ningún grupo matricial. Sin embargo, tiene una familia bien conocida de representaciones unitarias de dimensión infinita.

La conexión con el álgebra de Weyl

El álgebra de Lie $mathfrak{h}_n$ del grupo Heisenberg fue descrito anteriormente, (1), como álgebra de las matrices. El teorema Poincaré-Birkhoff-Witt se aplica para determinar el álgebra universal envolvente $U(mathfrak{h}_n)$ . Entre otras propiedades, el álgebra universal envolviendo es un álgebra asociativa en la que $mathfrak{h}_n$ inyectores.

Según el teorema de Poincaré-Birkhoff-Witt, es el espacio vectorial libre generado por los monomios

z^j p_1^{k_1} p_2^{k_2} cdots p_n^{k_n} q_1^{ell_1} q_2^{ell_2} cdots q_n^{ell_n} ~,

donde los exponentes son todos no negativos.

En consecuencia, $U(mathfrak{h}_n)$ consiste en polinomios reales

{displaystyle sum _{j,{vec {k}},{vec {ell }}}c_{j{vec {k}}{vec {ell }}},,z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}cdots p_{n}^{k_{n}}q_{1}^{ell _{1}}q_{2}^{ell _{2}}cdots q_{n}^{ell _{n}}~,}

con las relaciones de conmutación

p_k p_ell = p_ell p_k, quad q_k q_ell = q_ell q_k, quad p_k q_ell - q_ell p_k = delta_{k ell} z, quad z p_k - p_k z =0, quad z q_k - q_k z =0~.

El álgebra $U(mathfrak{h}_n)$ está estrechamente relacionado con el álgebra de operadores diferenciales en Rⁿ con coeficientes polinomio, ya que cualquier operador tiene una representación única en la forma

P=sum_{vec{k}, vec{ell}} c_{vec{k} vec{ell}} ,, partial_{x_1}^{k_1} partial_{x_2}^{k_2} cdots partial_{x_n}^{k_n} x_1^{ell_1} x_2^{ell_2} cdots x_n^{ell_n} ~.

Este álgebra se llama el álgebra Weyl. Sigue de tonterías abstractas que el álgebra de Weyl W_n es un cociente de $U(mathfrak{h}_n)$ . Sin embargo, esto también es fácil de ver directamente de las representaciones anteriores; viz.

z^j p_1^{k_1} p_2^{k_2} cdots p_n^{k_n} q_1^{ell_1} q_2^{ell_2} cdots q_n^{ell_n} , mapsto , partial_{x_1}^{k_1} partial_{x_2}^{k_2} cdots partial_{x_n}^{k_n} x_1^{ell_1} x_2^{ell_2} cdots x_n^{ell_n}~.

Aplicaciones

Did you mean:

Weyl 's parameterization of quantum mechanics

La aplicación que llevó a Hermann Weyl a una comprensión explícita del grupo de Heisenberg fue la pregunta de por qué el cuadro de Schrödinger y el cuadro de Heisenberg son físicamente equivalentes. De manera abstracta, la razón es el teorema de Stone-von Neumann: existe una representación unitaria única con la acción dada del elemento central del álgebra de Lie z, hasta una equivalencia unitaria: los elementos no triviales del álgebra son todos equivalente a los operadores habituales de posición y momento.

Por lo tanto, la imagen de Schrödinger y la imagen de Heisenberg son equivalentes: son simplemente formas diferentes de realizar esta representación esencialmente única.

Representación theta

David Mumford utilizó el mismo resultado de unicidad para grupos discretos de Heisenberg, en su teoría de ecuaciones que definen variedades abelianas. Esta es una gran generalización del enfoque utilizado en las funciones elípticas de Jacobi, que es el caso del grupo de Heisenberg módulo 2, de orden 8. El caso más simple es la representación theta del grupo de Heisenberg, del cual el caso discreto da la función theta.

Análisis de Fourier

El grupo de Heisenberg también aparece en el análisis de Fourier, donde se utiliza en algunas formulaciones del teorema de Stone-von Neumann. En este caso, se puede entender que el grupo de Heisenberg actúa sobre el espacio de funciones cuadradas integrables; el resultado es una representación de los grupos de Heisenberg, a veces llamada representación de Weyl.

Como variedad subriemanniana

El grupo tridimensional de Heisenberg H₃(R) en los reales también puede entenderse como una variedad suave, y específicamente, un ejemplo simple de variedad subriemanniana. Dado un punto p=(x,y,z) en R³, defina una forma 1 diferencial Θ en este punto como

{displaystyle Theta _{p}=dz-{frac {1}{2}}left(xdy-ydxright).}

Esta forma única pertenece al paquete cotangente de R³; eso es,

{displaystyle Theta _{p}:T_{p}mathbf {R} ^{3}to mathbf {R} }

es un mapa en el paquete tangente. Dejar

{displaystyle H_{p}=left{vin T_{p}mathbf {R} ^{3}mid Theta _{p}(v)=0right}.}

Se puede ver que H es un subbundeo del paquete tangente TR³. Un cometa H es dado por proyectar vectores al espacio bidimensional abarcado por vectores en los x y Sí. dirección. Es decir, vectores dados ${displaystyle v=(v_{1},v_{2},v_{3})}$ y ${displaystyle w=(w_{1},w_{2},w_{3})}$ en TR³, el producto interior es dado por

{displaystyle langle v,wrangle =v_{1}w_{1}+v_{2}w_{2}.}

La estructura resultante convierte H en la variedad del grupo de Heisenberg. Un marco ortonormal en la variedad está dado por los campos vectoriales de Lie.

{displaystyle {begin{aligned}X&={frac {partial }{partial x}}-{frac {1}{2}}y{frac {partial }{partial z}},\Y&={frac {partial }{partial y}}+{frac {1}{2}}x{frac {partial }{partial z}},\Z&={frac {partial }{partial z}},end{aligned}}}

que obedecen a las relaciones [X, Y] = Z y [X, Z ] = [Y, Z] = 0. Al ser campos vectoriales de Lie, forman una base invariante a la izquierda para la acción grupal. Las geodésicas del colector son espirales que se proyectan hasta formar círculos en dos dimensiones. Es decir, si

{displaystyle gamma (t)=(x(t),y(t),z(t))}

es una curva geodésica, luego la curva ${displaystyle c(t)=(x(t),y(t))}$ es un arco de un círculo, y

{displaystyle z(t)={frac {1}{2}}int _{c}xdy-ydx}

con la integral limitada al plano bidimensional. Es decir, la altura de la curva es proporcional al área del círculo subtendido por el arco circular, que sigue la curva de Stokes. teorema.

Grupo Heisenberg de un grupo abeliano localmente compacto

Es más generalmente posible definir el grupo Heisenberg de un grupo abeliano compacto localmente K, equipado con una medida Haar. Tal grupo tiene un doble Pontrjagin ${hat {K}}$ , que consiste en todo continuo $U(1)$ - caracteres valorados K, que es también un grupo abeliano localmente compacto si dotado con la topología compacta-abierto. The Heisenberg group associated with the locally compact abelian group K es el subgrupo del grupo unitario ${displaystyle L^{2}(K)}$ generada por traducciones de K y multiplicaciones por elementos ${hat {K}}$ .

En más detalle, el espacio Hilbert ${displaystyle L^{2}(K)}$ consiste en funciones de valor complejo integrado cuadrado $f$ on K. Las traducciones en K forma una representación unitaria K como operadores en ${displaystyle L^{2}(K)}$ :

{displaystyle (T_{x}f)(y)=f(x+y)}

para ${displaystyle x,yin K}$ . Así también las multiplicaciones por caracteres:

{displaystyle (M_{chi }f)(y)=chi (y)f(y)}

para ${displaystyle chi in {hat {K}}}$ . Estos operadores no se comunican, y en cambio satisfacen

{displaystyle left(T_{x}M_{chi }T_{x}^{-1}M_{chi }^{-1}fright)(y)={overline {chi (x)}}f(y)}

multiplicación por un número complejo de módulo unitario fijo.

Así que el grupo Heisenberg ${displaystyle H(K)}$ asociado con K es un tipo de extensión central ${displaystyle Ktimes {hat {K}}}$ , a través de una secuencia exacta de grupos:

{displaystyle 1to U(1)to H(K)to Ktimes {hat {K}}to 0.}

Más general Los grupos de Heisenberg son descritos por 2 cocitos en el grupo de cohomología ${displaystyle H^{2}(K,U(1))}$ . La existencia de una dualidad entre $K$ y ${hat {K}}$ da lugar a un cociclo canónico, pero generalmente hay otros.

El grupo Heisenberg actúa irreductiblemente ${displaystyle L^{2}(K)}$ . De hecho, los caracteres continuos separan puntos por lo que cualquier operador unitario de ${displaystyle L^{2}(K)}$ que se comunica con ellos es un $L^{infty }$ multiplicador. Pero la comunicación con traducciones implica que el multiplicador es constante.

Una versión del teorema Stone-von Neumann, probada por George Mackey, sostiene para el grupo Heisenberg ${displaystyle H(K)}$ . El transformado Fourier es el único entrelazador entre las representaciones de ${displaystyle L^{2}(K)}$ y ${displaystyle L^{2}left({hat {K}}right)}$ . Ver la discusión en Stone–von Neumann teorem#Relación a la transformación Fourier para detalles.