Gráfico dual

En la disciplina matemática de la teoría de grafos, el gráfico dual de un gráfico plano G es un gráfico que tiene un vértice para cada cara de G. El gráfico dual tiene una arista para cada par de caras en G que están separadas entre sí por una arista y una bucle cuando aparece la misma cara en ambos lados de un borde. Por lo tanto, cada borde e de G tiene un borde dual correspondiente, cuyos puntos finales son los vértices duales correspondientes a las caras a cada lado de e. La definición del dual depende de la elección de incrustación del gráfico G, por lo que es una propiedad de los gráficos planos (gráficos que ya están incrustados en el plano) en lugar de gráficos planos (gráficos que pueden estar incrustados pero cuya incrustación aún no se conoce). En general, para los gráficos planos, puede haber múltiples gráficos duales, dependiendo de la elección de la incrustación plana del gráfico.

Históricamente, la primera forma de dualidad gráfica que se reconoció fue la asociación de los sólidos platónicos en pares de poliedros duales. La dualidad de gráficos es una generalización topológica de los conceptos geométricos de poliedros duales y teselaciones duales y, a su vez, se generaliza combinatoriamente mediante el concepto de matroide dual. Las variaciones de la dualidad de gráficos planos incluyen una versión de dualidad para gráficos dirigidos y dualidad para gráficos incrustados en superficies bidimensionales no planas.

Estas nociones de gráficos duales no deben confundirse con una noción diferente, el gráfico lineal o dual de borde a vértice de un gráfico.

El término dual se usa porque la propiedad de ser un gráfico dual es simétrico, lo que significa que si H es un dual de un gráfico conectado G, luego G es un dual de H. Cuando se analiza el dual de un gráfico G, el gráfico G en sí mismo puede denominarse "gráfico primario". Muchas otras propiedades y estructuras de los gráficos pueden traducirse en otras propiedades y estructuras naturales del dual. Por ejemplo, los ciclos son duales con los cortes, los árboles de expansión son duales con los complementos de los árboles de expansión y los gráficos simples (sin aristas paralelas ni bucles propios) son duales con los gráficos conectados de 3 aristas.

La dualidad gráfica puede ayudar a explicar la estructura de laberintos y cuencas de drenaje. Los gráficos duales también se han aplicado en visión por computadora, geometría computacional, generación de mallas y diseño de circuitos integrados.

Ejemplos

Ciclos y dipolos

Un gráfico dipole

Un gráfico de ciclo

La incrustación plana única de un gráfico de ciclo divide el plano en solo dos regiones, el interior y el exterior del ciclo, según el teorema de la curva de Jordan. Sin embargo, en un ciclo n, estas dos regiones están separadas entre sí por n bordes diferentes. Por lo tanto, el gráfico dual del n-ciclo es un multigrafo con dos vértices (duales a las regiones), conectados entre sí. por n bordes duales. Un gráfico de este tipo se denomina gráfico de aristas múltiples, de enlace o, a veces, de dipolo. Por el contrario, el gráfico dipolo de borde dual a n es un n-ciclo.

Poliedros duales

De acuerdo con el teorema de Steinitz, cada gráfico poliedral (el gráfico formado por los vértices y bordes de un poliedro convexo tridimensional) debe ser planar y 3-vertex-conectado, y cada gráfico plano de 3 vértigos conectado viene de un poliedro convexo de esta manera. Cada poliedro convexo tridimensional tiene un poliedro dual; el poliedro dual tiene un vértice para cada cara del poliedro original, con dos vértices duales adyacentes cada vez que las dos caras correspondientes comparten un borde. Cada vez que dos polihedra son duales, sus gráficos también son duales. Por ejemplo, los sólidos platónicos vienen en pares duales, con el octaedro dual al cubo, el dodecaedro dual al icosahedro, y el tetraedro dual a sí mismo. La dualidad de poliedro también puede extenderse a la dualidad de politopos dimensionales superiores, pero esta extensión de la dualidad geométrica no tiene conexiones claras a la dualidad gráfica-teorética.

Gráficos autoduales

Se dice que un gráfico plano es autodual si es isomorfo a su gráfico dual. Los gráficos de rueda proporcionan una familia infinita de gráficos autoduales provenientes de poliedros autoduales (las pirámides). Sin embargo, también existen gráficos autoduales que no son poliédricos, como el que se muestra. Servacio y Christopher (1992) describe dos operaciones, adhesión y explosión, que pueden usarse para construir un gráfico autodual que contenga un gráfico plano determinado; por ejemplo, el gráfico autodual que se muestra se puede construir como la adhesión de un tetraedro con su dual.

De la fórmula de Euler se deduce que cada gráfico autodual con n vértices tiene exactamente 2n − 2 aristas. Cada gráfico plano autodual simple contiene al menos cuatro vértices de grado tres, y cada incrustación autodual tiene al menos cuatro caras triangulares.

Propiedades

Muchos conceptos naturales e importantes en la teoría de grafos corresponden a otros conceptos igualmente naturales pero diferentes en la gráfica dual. Debido a que el dual del dual de un gráfico plano conectado es isomorfo al gráfico primario, cada uno de estos pares es bidireccional: if concept X en un gráfico plano corresponde al concepto Y en el gráfico dual, luego al concepto Y en un gráfico plano corresponde al concepto X en el dual.

Gráficos simples y multigráficos

El dual de un gráfico simple no tiene por qué ser simple: puede tener bucles automáticos (una arista con ambos extremos en el mismo vértice) o múltiples aristas que conectan los mismos dos vértices, como ya era evidente en el ejemplo de los multigrafos dipolares. siendo dual para ciclo de gráficos. Como caso especial de la dualidad del ciclo de corte que se analiza a continuación, los puentes de un gráfico plano G están en correspondencia uno a uno con los bucles automáticos del gráfico dual. Por la misma razón, un par de aristas paralelas en un multigrafo dual (es decir, un ciclo de longitud 2) corresponde a un conjunto de corte de 2 aristas en el gráfico primario (un par de aristas cuya eliminación desconecta el gráfico). Por lo tanto, un gráfico plano es simple si y sólo si su dual no tiene conjuntos de cortes de 1 o 2 aristas; es decir, si está conectado a 3 aristas. Los gráficos planos simples cuyos duales son simples son exactamente los gráficos planos simples conectados con 3 aristas. Esta clase de gráficos incluye, pero no es lo mismo, la clase de gráficos planos simples conectados por 3 vértices. Por ejemplo, la figura que muestra un gráfico autodual está conectada por 3 aristas (y por lo tanto su dual es simple) pero no está conectada por 3 vértices.

Singularidad

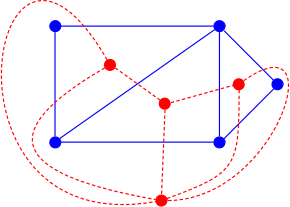
Debido a que el gráfico dual depende de una incrustación particular, el gráfico dual de un gráfico plano no es único, en el sentido de que el mismo gráfico plano puede tener gráficos duales no isomorfos. En la imagen, los gráficos azules son isomórficos pero sus gráficos duales rojos no lo son. El dual rojo superior tiene un vértice con grado 6 (correspondiente a la cara exterior del gráfico azul) mientras que en el gráfico rojo inferior todos los grados son menores que 6.

Hassler Whitney demostró que si el gráfico tiene 3 conexos, entonces la incrustación y, por tanto, el gráfico dual, es único. Según el teorema de Steinitz, estas gráficas son exactamente las gráficas poliédricas, las gráficas de poliedros convexos. Un gráfico plano está conectado a 3 vértices si y solo si su gráfico dual está conectado a 3 vértices. De manera más general, un gráfico plano tiene una incrustación única y, por lo tanto, también un dual único, si y solo si es una subdivisión de un gráfico plano conectado de 3 vértices (un gráfico formado a partir de un gráfico plano conectado de 3 vértices reemplazando algunos de sus bordes por senderos). Para algunos gráficos planos que no están conectados por 3 vértices, como el gráfico bipartito completo K_2,4, la incrustación no es única, pero todas las incrustaciones son isomorfas. Cuando esto sucede, correspondientemente, todos los gráficos duales son isomórficos.

Debido a que diferentes incrustaciones pueden conducir a diferentes gráficos duales, probar si un gráfico es dual de otro (sin conocer ya sus incrustaciones) es un problema algorítmico no trivial. Para gráficos biconectados, se puede resolver en tiempo polinómico utilizando los árboles SPQR de los gráficos para construir una forma canónica para la relación de equivalencia de tener un dual mutuo compartido. Por ejemplo, los dos gráficos rojos de la ilustración son equivalentes según esta relación. Sin embargo, para gráficos planos que no son biconexos, esta relación no es una relación de equivalencia y el problema de probar la dualidad mutua es NP-completo.

Cortes y ciclos

Un conjunto de cortes en un gráfico conectado arbitrario es un subconjunto de aristas definidas a partir de una partición de los vértices en dos subconjuntos, al incluir una arista en el subconjunto cuando tiene un punto final a cada lado de la partición. Eliminar los bordes de un cutset necesariamente divide el gráfico en al menos dos componentes conectados. Un conjunto de cortes mínimo (también llamado enlace) es un conjunto de cortes con la propiedad de que cada subconjunto adecuado del conjunto de cortes no es en sí mismo un corte. Un conjunto de cortes mínimo de un gráfico conectado necesariamente separa su gráfico en exactamente dos componentes y consta del conjunto de aristas que tienen un punto final en cada componente. Un ciclo simple es un subgrafo conexo en el que cada vértice del ciclo incide exactamente en dos aristas del ciclo.

En un gráfico plano conectado G, cada ciclo simple de G corresponde a un cutset mínimo en el dual de G, y viceversa. Esto puede verse como una forma del teorema de la curva de Jordan: cada ciclo simple separa las caras de G en las caras del interior. del ciclo y las caras del exterior del ciclo, y los duales de las aristas del ciclo son exactamente las aristas que cruzan del interior al exterior. La circunferencia de cualquier gráfico plano (el tamaño de su ciclo más pequeño) es igual a la conectividad de bordes de su gráfico dual (el tamaño de su conjunto de corte más pequeño).

Esta dualidad se extiende desde cortes y ciclos individuales hasta espacios vectoriales definidos a partir de ellos. El espacio de ciclo de un gráfico se define como la familia de todos los subgrafos que tienen grados pares en cada vértice; puede verse como un espacio vectorial sobre el campo finito de dos elementos, con la diferencia simétrica de dos conjuntos de aristas actuando como la operación de suma vectorial en el espacio vectorial. De manera similar, el espacio de corte de un gráfico se define como la familia de todos los conjuntos de corte, y la suma de vectores se define de la misma manera. Entonces el espacio de ciclo de cualquier gráfico plano y el espacio de corte de su gráfico dual son isomórficos como espacios vectoriales. Por tanto, el rango de un gráfico plano (la dimensión de su espacio de corte) es igual al número ciclotómico de su dual (la dimensión de su espacio de ciclo) y viceversa. Una base de ciclo de un gráfico es un conjunto de ciclos simples que forman una base del espacio de ciclos (cada subgrafo de grado par se puede formar exactamente de una manera como una diferencia simétrica de algunos de estos ciclos). Para gráficos planos ponderados por bordes (con pesos suficientemente generales como para que no haya dos ciclos que tengan el mismo peso), la base del ciclo de peso mínimo del gráfico es dual al árbol Gomory-Hu del gráfico dual, una colección de cortes anidados que juntos incluyen un corte mínimo que separa cada par de vértices del gráfico. Cada ciclo en la base del ciclo de peso mínimo tiene un conjunto de aristas que son duales a las aristas de uno de los cortes en el árbol Gomory-Hu. Cuando los pesos del ciclo pueden estar vinculados, la base del ciclo de peso mínimo puede no ser única, pero en este caso sigue siendo cierto que el árbol Gomory-Hu del gráfico dual corresponde a una de las bases del ciclo de peso mínimo del gráfico.

En los gráficos planos dirigidos, los ciclos dirigidos simples son cortes duales a dirigidos (divisiones de los vértices en dos subconjuntos de modo que todos los bordes van en una dirección, de un subconjunto al otro). Los gráficos planos fuertemente orientados (gráficos cuyo gráfico subyacente no dirigido está conectado y en los que cada arista pertenece a un ciclo) son gráficos duales a acíclicos dirigidos en los que ninguna arista pertenece a un ciclo. Para decirlo de otra manera, las orientaciones fuertes de un gráfico plano conectado (asignaciones de direcciones a los bordes del gráfico que dan como resultado un gráfico fuertemente conectado) son duales a las orientaciones acíclicas (asignaciones de direcciones que producen un gráfico acíclico dirigido). De la misma manera, los dijoins (conjuntos de aristas que incluyen una arista de cada corte dirigido) son conjuntos de arcos de retroalimentación duales (conjuntos de aristas que incluyen una arista de cada ciclo).

Árboles de expansión

Un árbol de expansión puede definirse como un conjunto de aristas que, junto con todos los vértices del gráfico, forman un subgrafo conectado y acíclico. Pero, por dualidad de ciclo de corte, si un conjunto S de aristas en un gráfico plano G es acíclico (no tiene ciclos), entonces el conjunto de aristas es dual a S no tiene cortes, de lo que se deduce que el conjunto complementario de aristas duales (los duales de las aristas que no están en S) forma un subgrafo conectado. Simétricamente, si S está conectado, entonces las aristas se duplican al complemento de S forma un subgrafo acíclico. Por lo tanto, cuando S tiene ambas propiedades (es conexo y acíclico), lo mismo ocurre con el conjunto complementario en el grafo dual. Es decir, cada árbol de expansión de G es complementario a un árbol de expansión del grafo dual, y viceversa. Por lo tanto, los bordes de cualquier gráfico plano y su dual se pueden dividir juntos (de múltiples maneras diferentes) en dos árboles de expansión, uno en el primario y otro en el dual, que juntos se extienden a todos los vértices y caras del gráfico, pero nunca cruzarse entre sí. En particular, el árbol de expansión mínimo de G es complementario al árbol de expansión máximo del gráfico dual. Sin embargo, esto no funciona para árboles de camino más corto, ni siquiera aproximadamente: existen gráficos planos tales que, por cada par de un árbol de expansión en el gráfico y un árbol de expansión complementario en el gráfico dual, al menos uno de los dos árboles tiene distancias que son significativamente más largas que las distancias en su gráfico.

Un ejemplo de este tipo de descomposición en árboles interdigitados se puede ver en algunos tipos de laberintos simples, con una única entrada y sin componentes desconectados de sus paredes. En este caso, tanto las paredes del laberinto como el espacio entre las paredes toman la forma de un árbol matemático. Si el espacio libre del laberinto se divide en celdas simples (como los cuadrados de una cuadrícula), entonces este sistema de celdas puede verse como una incorporación de un gráfico plano, en el que la estructura de árbol de las paredes forma un árbol de expansión de el gráfico y la estructura de árbol del espacio libre forman un árbol de expansión del gráfico dual. También se pueden ver pares similares de árboles entrelazados en el patrón en forma de árbol de arroyos y ríos dentro de una cuenca de drenaje y en el patrón dual en forma de árbol de las crestas que separan los arroyos.

Esta partición de las aristas y sus duales en dos árboles conduce a una prueba simple de la fórmula de Euler V − E + F = 2 para gráficos planos con V vértices, E aristas y F caras. Cualquier árbol de expansión y su árbol de expansión dual complementario dividen los bordes en dos subconjuntos de V − 1 y F − 1 aristas respectivamente, y sumando los tamaños de los dos subconjuntos se obtiene la ecuación

E =V −1) + (F −1)

que puede reorganizarse para formar la fórmula de Euler. Según Duncan Sommerville, esta demostración de la fórmula de Euler se debe a la Geometrie der Lage de K. G. C. Von Staudt (Núremberg, 1847).

En incrustaciones de superficies no planas, el conjunto de aristas duales complementarias a un árbol de expansión no es un árbol de expansión dual. En cambio, este conjunto de aristas es la unión de un árbol de expansión dual con un pequeño conjunto de aristas adicionales cuyo número está determinado por el género de la superficie en la que está incrustado el gráfico. Los bordes adicionales, en combinación con caminos en los árboles de expansión, se pueden utilizar para generar el grupo fundamental de la superficie.

Propiedades adicionales

Cualquier fórmula de conteo que involucre vértices y caras que sea válida para todos los gráficos planos puede transformarse mediante dualidad plana en una fórmula equivalente en la que se hayan intercambiado los roles de los vértices y las caras. La fórmula de Euler, que es autodual, es un ejemplo. Otro dado por Harary implica el lema del apretón de manos, según el cual la suma de los grados de los vértices de cualquier gráfico es igual al doble del número de aristas. En su forma dual, este lema establece que en un gráfico plano, la suma del número de lados de las caras del gráfico es igual al doble del número de aristas.

La gráfica medial de una gráfica plana es isomorfa a la gráfica medial de su dual. Dos gráficos planos pueden tener gráficos mediales isomórficos sólo si son duales entre sí.

Un gráfico plano con cuatro o más vértices es máximo (no se pueden agregar más aristas mientras se preserva la planaridad) si y solo si su gráfico dual está conectado por 3 vértices y es 3 regular.

Un grafo plano conexo es euleriano (tiene grado par en cada vértice) si y sólo si su grafo dual es bipartito. Un ciclo hamiltoniano en un grafo plano G corresponde a una partición de los vértices del grafo dual en dos subconjuntos (el interior y el exterior). del ciclo) cuyos subgrafos inducidos son ambos árboles. En particular, la conjetura de Barnette sobre la hamiltonicidad de los gráficos poliédricos bipartitos cúbicos es equivalente a la conjetura de que todo gráfico plano máximo euleriano puede dividirse en dos árboles inducidos.

Si un gráfico plano G tiene un polinomio de Tutte T _G(x,y), entonces el polinomio de Tutte de su gráfica dual se obtiene mediante intercambiando x y y . Por esta razón, si algún valor particular del polinomio de Tutte proporciona información sobre ciertos tipos de estructuras en G, entonces intercambiar los argumentos a el polinomio de Tutte dará la información correspondiente para las estructuras duales. Por ejemplo, el número de orientaciones fuertes es T_G(0,2) y el número de orientaciones acíclicas es T_G(2,0). Para gráficos planos sin puente, los colores de los gráficos con colores k corresponden a un módulo de flujos en ninguna parte cero k en el gráfico dual. Por ejemplo, el teorema de los cuatro colores (la existencia de 4 colores para cada gráfico plano) se puede expresar de manera equivalente afirmando que el dual de cada gráfico plano sin puente tiene un flujo 4 en ninguna parte cero. El número de k-coloraciones se cuenta (hasta un factor fácilmente calculable) mediante el valor del polinomio de Tutte T_G(1 − k,0) y dualmente el número de ninguna parte- cero k-flujos se cuentan por T_G(0,1 − k).

Un gráfico st-planar es un gráfico plano conectado junto con una orientación bipolar de ese gráfico, una orientación que lo hace acíclico con una sola fuente y un solo sumidero, los cuales deben estar en la misma cara que cada uno otro. Un gráfico de este tipo se puede convertir en un gráfico fuertemente conectado agregando un borde más, desde el sumidero hasta la fuente, a través de la cara exterior. El dual de este gráfico plano aumentado es en sí mismo el aumento de otro gráfico st-planar.

Variaciones

Gráficos dirigidos

En un gráfico plano dirigido, el gráfico dual también puede hacerse dirigido, orientando cada borde dual con un giro de 90° en el sentido de las agujas del reloj desde el borde primario correspondiente. Estrictamente hablando, esta construcción no es una dualidad de grafos planos dirigidos, porque partir de un grafo G y tomar el dual dos veces no regresa al propio G, pero en su lugar construye un gráfico isomorfo al gráfico transpuesto de G, el gráfico formado a partir de G invirtiendo todos sus bordes. Al tomar el dual cuatro veces se regresa al gráfico original.

Dual débil

El dual débil de un gráfico plano es el subgrafo del gráfico dual cuyos vértices corresponden a las caras acotadas del gráfico primario. Un grafo plano es plano exterior si y sólo si su dual débil es un bosque. Para cualquier gráfico plano G, sea G⁺ sea el multigrafo plano formado agregando un único vértice nuevo v en la cara ilimitada de G y conectando v a cada vértice de la cara exterior (varias veces, si un vértice aparece varias veces en el límite de la cara exterior); entonces, G es el dual débil del dual (plano) de G⁺.

Gráficos y teselados infinitos

El concepto de dualidad se aplica tanto a gráficos infinitos incrustados en el plano como a gráficos finitos. Sin embargo, se necesita cuidado para evitar complicaciones topológicas como puntos del plano que no son parte de una región abierta separada del gráfico ni parte de un borde o vértice del gráfico. Cuando todas las caras son regiones delimitadas rodeadas por un ciclo del gráfico, una incrustación infinita de un gráfico plano también puede verse como una teselación del plano, una cobertura del plano por discos cerrados (los mosaicos de la teselación) cuyos interiores (las caras de la incrustación) son discos abiertos separados. La dualidad plana da lugar a la noción de teselación dual, una teselación formada colocando un vértice en el centro de cada mosaico y conectando los centros de los mosaicos adyacentes.

El concepto de teselación dual también se puede aplicar a particiones del plano en un número finito de regiones. En este caso, está estrechamente relacionado, pero no es exactamente lo mismo, con la dualidad del gráfico plano. Por ejemplo, el diagrama de Voronoi de un conjunto finito de sitios puntuales es una partición del plano en polígonos dentro de los cuales un sitio está más cerca que cualquier otro. Los sitios en el casco convexo de la entrada dan lugar a polígonos de Voronoi ilimitados, dos de cuyos lados son rayos infinitos en lugar de segmentos de recta finitos. El dual de este diagrama es la triangulación de Delaunay de la entrada, un gráfico plano que conecta dos sitios por un borde siempre que exista un círculo que contenga esos dos sitios y ningún otro sitio. Los bordes del casco convexo de la entrada también son bordes de la triangulación de Delaunay, pero corresponden a rayos en lugar de segmentos de línea del diagrama de Voronoi. Esta dualidad entre diagramas de Voronoi y triangulaciones de Delaunay se puede convertir en una dualidad entre gráficos finitos de dos maneras: agregando un vértice artificial en el infinito al diagrama de Voronoi, para que sirva como otro punto final para todos sus rayos, o tratando la parte acotada del diagrama de Voronoi como el dual débil de la triangulación de Delaunay. Aunque el diagrama de Voronoi y la triangulación de Delaunay son duales, su incrustación en el plano puede tener cruces adicionales más allá de los cruces de pares duales de aristas. Cada vértice del triángulo de Delaunay se sitúa dentro de su cara correspondiente del diagrama de Voronoi. Cada vértice del diagrama de Voronoi está situado en el circuncentro del triángulo correspondiente de la triangulación de Delaunay, pero este punto puede estar fuera de su triángulo.

Incrustaciones no planas

K₇ es dual al gráfico Heawood en el torus

K₆ es dual al gráfico Petersen en el plano proyector

El concepto de dualidad se puede ampliar para graficar incrustaciones en variedades bidimensionales distintas del plano. La definición es la misma: hay un vértice dual para cada componente conectado del complemento del gráfico en la variedad, y un borde dual para cada borde del gráfico que conecta los dos vértices duales a cada lado del borde. En la mayoría de las aplicaciones de este concepto, se restringe a incrustaciones con la propiedad de que cada cara es un disco topológico; esta restricción generaliza el requisito de que los gráficos planos sean conectados. Con esta restricción, el dual de cualquier gráfico incrustado en una superficie tiene una incrustación natural en la misma superficie, de modo que el dual del dual es isomórfico y está isomórficamente incrustado en el gráfico original. Por ejemplo, el gráfico completo K₇ es un gráfico toroidal: no es plano pero puede estar incrustado en un toroide. , siendo cada cara de la incrustación un triángulo. Esta incorporación tiene el gráfico de Heawood como gráfico dual.

El mismo concepto funciona igualmente bien para superficies no orientables. Por ejemplo, K₆ puede estar incrustado en el plano proyectivo con diez caras triangulares como el hemiicosaedro, cuyo dual es el gráfico de Petersen incrustado como el hemidodecaedro.

Incluso los gráficos planos pueden tener incorporaciones no planas, con duales derivados de aquellas incorporaciones que difieren de sus duales planos. Por ejemplo, los cuatro polígonos de Petrie de un cubo (hexágonos formados eliminando dos vértices opuestos del cubo) forman las caras hexagonales de una incrustación del cubo en un toro. El gráfico dual de esta incrustación tiene cuatro vértices que forman un gráfico completo K₄ con aristas duplicadas. En la incrustación del toroide de este gráfico dual, las seis aristas incidentes en cada vértice, en orden cíclico alrededor de ese vértice, pasan dos veces por los otros tres vértices. A diferencia de la situación en el plano, esta incrustación del cubo y su dual no es única; el gráfico cúbico tiene varias otras incrustaciones de toros, con diferentes duales.

Muchas de las equivalencias entre las propiedades de los gráficos primarios y duales de los gráficos planos no se generalizan a duales no planos o requieren cuidado adicional en su generalización.

Otra operación en gráficos incrustados en superficies es el dual de Petrie, que utiliza los polígonos de Petrie de la incrustación como las caras de una nueva incrustación. A diferencia del gráfico dual habitual, tiene los mismos vértices que el gráfico original, pero generalmente se encuentra en una superficie diferente. La dualidad de superficie y la dualidad de Petrie son dos de las seis operaciones de Wilson y juntas generan el grupo de estas operaciones.

Matroides y duales algebraicas

Un dual algebraico de un gráfico conexo G es un gráfico G^* tal que G y G^* tienen el mismo conjunto de aristas, cualquier ciclo de G es un corte de G^*, y cualquier corte de G es un ciclo de G^* . Cada gráfico plano tiene un dual algebraico, que en general no es único (cualquier dual definido por una incrustación plana servirá). En realidad, lo contrario es cierto, como lo establece Hassler Whitney en el criterio de planaridad de Whitney:

Un gráfico conectado G es planar si y sólo si tiene un dual algebraico.

El mismo hecho se puede expresar en la teoría de las matroides. Si M es la matriz gráfica de un gráfico G, entonces un gráfico G^* es un dual algebraico de G si y sólo si el matroide gráfico de G^* es la matroide dual de M. Entonces, el criterio de planaridad de Whitney puede reformularse afirmando que la matroide dual de una matroide gráfica M es en sí misma una matroide gráfica. si y sólo si el gráfico subyacente G de M es plano. Si G es plano, la matroide dual es la matroide gráfica del gráfico dual de G. En particular, todos los gráficos duales, para todas las diferentes incrustaciones planas de G, tienen matroides gráficas isomorfas.

Para incrustaciones de superficies no planas, a diferencia de los duales planos, el gráfico dual generalmente no es un dual algebraico del gráfico primario. Y para un gráfico no plano G, la matroide dual de la matroide gráfica de G no es en sí mismo un matroide gráfico. Sin embargo, sigue siendo una matroide cuyos circuitos corresponden a los cortes en G, y en este sentido se puede considerar como un sistema combinatorio. Dual algebraico generalizado de G.

La dualidad entre gráficos planos eulerianos y bipartitos se puede extender a matroides binarias (que incluyen las matroides gráficas derivadas de gráficos planos): una matroide binaria es euleriana si y sólo si su matroide dual es bipartita.

Los dos conceptos duales de circunferencia y conectividad de bordes están unificados en la teoría matroide mediante la circunferencia de matroide: la circunferencia de la matroide gráfica de un gráfico plano es la misma que la circunferencia del gráfico, y la circunferencia de la matroide dual (la matroide gráfica del gráfico dual) es la conectividad de borde del gráfico.

Aplicaciones

Junto con su uso en la teoría de grafos, la dualidad de los gráficos planos tiene aplicaciones en varias otras áreas del estudio matemático y computacional.

En los sistemas de información geográfica, las redes de flujo (como las redes que muestran cómo fluye el agua en un sistema de arroyos y ríos) son duales a las redes celulares que describen divisiones de drenaje. Esta dualidad se puede explicar modelando la red de flujo como un árbol de expansión en un gráfico de cuadrícula de una escala apropiada, y modelando la división de drenaje como el árbol de expansión complementario de las crestas en el gráfico de cuadrícula dual.

En la visión por computadora, las imágenes digitales se dividen en pequeños píxeles cuadrados, cada uno de los cuales tiene su propio color. La gráfica dual de esta subdivisión en cuadrados tiene un vértice por píxel y una arista entre pares de píxeles que comparten una arista; Es útil para aplicaciones que incluyen la agrupación de píxeles en regiones conectadas de colores similares.

En geometría computacional, la dualidad entre los diagramas de Voronoi y las triangulaciones de Delaunay implica que cualquier algoritmo para construir un diagrama de Voronoi puede convertirse inmediatamente en un algoritmo para la triangulación de Delaunay, y viceversa. La misma dualidad también se puede utilizar en la generación de mallas de elementos finitos. El algoritmo de Lloyd, un método basado en diagramas de Voronoi para mover un conjunto de puntos en una superficie a posiciones más uniformemente espaciadas, se usa comúnmente como una forma de suavizar una malla de elementos finitos descrita por la triangulación dual de Delaunay. Este método mejora la malla haciendo que sus triángulos tengan un tamaño y una forma más uniformes.

En la síntesis de circuitos CMOS, la función a sintetizar se representa como una fórmula en álgebra booleana. Luego, esta fórmula se traduce en dos multigrafos en serie-paralelos. Estos gráficos pueden interpretarse como diagramas de circuitos en los que los bordes de los gráficos representan transistores, controlados por las entradas a la función. Un circuito calcula la función en sí y el otro calcula su complemento. Uno de los dos circuitos se obtiene convirtiendo las conjunciones y disyunciones de la fórmula en composiciones de gráficos en serie y en paralelo, respectivamente. El otro circuito invierte esta construcción, convirtiendo las conjunciones y disyunciones de la fórmula en composiciones de gráficos en paralelo y en serie. Estos dos circuitos, aumentados por un borde adicional que conecta la entrada de cada circuito con su salida, son gráficos duales planos.

Historia

La dualidad de los poliedros convexos fue reconocida por Johannes Kepler en su libro de 1619 Harmonices Mundi. Gráficos duales planos reconocibles, fuera del contexto de los poliedros, aparecieron ya en 1725, en la obra publicada póstumamente de Pierre Varignon, Nouvelle Méchanique ou Statique. Esto fue incluso antes del trabajo de Leonhard Euler de 1736 sobre los Siete Puentes de Königsberg, que a menudo se considera el primer trabajo sobre teoría de grafos. Varignon analizó las fuerzas sobre sistemas estáticos de puntales dibujando un gráfico dual a los puntales, con longitudes de borde proporcionales a las fuerzas sobre los puntales; este gráfico dual es un tipo de diagrama de Cremona. En relación con el teorema de los cuatro colores, Alfred Kempe mencionó las gráficas duales de mapas (subdivisiones del plano en regiones) en 1879, y Lothar Heffter las extendió a mapas sobre superficies no planas. "font-size:85%; font-style: normal;"> [de] en 1891. Hassler Whitney introdujo la dualidad como operación en gráficos planos abstractos en 1931.