Gráfico de complemento

En el campo matemático de la teoría de grafos, el complemento o inverso de un gráfico G es un gráfico H en los mismos vértices tal que dos vértices distintos de H son adyacentes si y sólo si no son adyacentes en G. Es decir, para generar el complemento de un gráfico, se completan todos los bordes faltantes necesarios para formar un gráfico completo y se eliminan todos los bordes que estaban allí anteriormente.

El complemento no es el complemento establecido del gráfico; sólo se complementan los bordes.

Definición

Sea G = (V, E) un gráfico simple y sea K consta de todos los subconjuntos de 2 elementos de V. Entonces H = (V, K E) es el complemento de G, donde K E es el complemento relativo de E en K. Para gráficos dirigidos, el complemento se puede definir de la misma manera, como un gráfico dirigido en el mismo conjunto de vértices, utilizando el conjunto de todos los pares ordenados de 2 elementos de V en lugar del conjunto K en la fórmula anterior. En términos de la matriz de adyacencia A del gráfico, si Q es la matriz de adyacencia del gráfico completo del mismo número de vértices (es decir, todas las entradas son la unidad excepto la diagonal entradas que son cero), entonces la matriz de adyacencia del complemento de A es Q-A.

El complemento no está definido para multigrafos. En gráficos que permiten bucles automáticos (pero no adyacencias múltiples), el complemento de G se puede definir agregando un bucle automático a cada vértice que no tenga uno en G, y de lo contrario usando la misma fórmula que arriba. Sin embargo, esta operación es diferente de la de gráficos simples, ya que aplicarla a un gráfico sin bucles automáticos daría como resultado un gráfico con bucles automáticos en todos los vértices.

Aplicaciones y ejemplos

Varios conceptos de la teoría de grafos están relacionados entre sí mediante complementación:

• El complemento de un gráfico sin borde es un gráfico completo y viceversa.
• Cualquier subgrafo inducido del gráfico complementario de un gráfico G es el complemento del subgrafo inducido correspondiente G.
• Un conjunto independiente en un gráfico es una camarilla en el gráfico complementario y viceversa. Este es un caso especial de las dos propiedades anteriores, ya que un conjunto independiente es un subgrafo inducido sin borde y una camarilla es un subgrafo inducido completo.
• El grupo automorfismo de un gráfico es el grupo automorfismo de su complemento.
• El complemento de cada gráfico sin triángulo es un gráfico libre de garras, aunque el reverso no es cierto.

Gráficos y clases de gráficos autocomplementarios

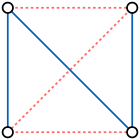
Un grafo autocomplementario es un grafo isomorfo a su propio complemento. Los ejemplos incluyen el gráfico de ruta de cuatro vértices y el gráfico de ciclo de cinco vértices. No existe una caracterización conocida de gráficos autocomplementarios.

Varias clases de gráficos son autocomplementarias, en el sentido de que el complemento de cualquier gráfico en una de estas clases es otro gráfico en la misma clase.

• Los gráficos perfectos son los gráficos en los que, por cada subgrafo inducido, el número cromático equivale al tamaño de la camarilla máxima. El hecho de que el complemento de un gráfico perfecto también es perfecto es el teorema gráfico perfecto de László Lovász.
• Los cógrafos se definen como los gráficos que pueden ser construidos a partir de vértices individuales por operaciones de unión y complementación descomunadas. Forman una familia autocomplementaria de gráficos: el complemento de cualquier cograph es otro cograph diferente. Para los gráficos de más de un vértice, exactamente un gráfico en cada par complementario está conectado, y una definición equivalente de los gráficos es que cada uno de sus subgrafos inducidos conectados tiene un complemento desconectado. Otra definición autocomplementaria es que son los gráficos sin subgrafo inducido en la forma de un camino de cuatro-vertex.
• Otra clase autocomplementaria de gráficos es la clase de gráficos divididos, los gráficos en los que los vértices pueden dividirse en una camarilla y un conjunto independiente. La misma partición da un conjunto independiente y una camarilla en el gráfico de complemento.
• Los gráficos umbral son los gráficos formados por añadir repetidamente un vértice independiente (uno sin vecinos) o un vértice universal (adyacente a todos los vértices previamente añadidos). Estas dos operaciones son complementarias y generan una clase autocomplementaria de gráficos.

Aspectos algorítmicos

En el análisis de algoritmos sobre gráficos, la distinción entre un gráfico y su complemento es importante, porque un gráfico disperso (uno con un número pequeño de aristas en comparación con el número de pares de vértices) en general no tendrá un complemento escaso, por lo que un algoritmo que requiere un tiempo proporcional al número de aristas en un gráfico determinado puede tardar una cantidad de tiempo mucho mayor si el mismo algoritmo se ejecuta en una representación explícita del gráfico de complemento. Por lo tanto, los investigadores han estudiado algoritmos que realizan cálculos gráficos estándar en el complemento de un gráfico de entrada, utilizando una representación gráfica implícita que no requiere la construcción explícita del gráfico complementario. En particular, es posible simular una búsqueda en profundidad o una búsqueda en amplitud en el gráfico complementario, en una cantidad de tiempo que es lineal en el tamaño del gráfico dado, incluso cuando el gráfico complementario puede tener un tamaño mucho mayor.. También es posible utilizar estas simulaciones para calcular otras propiedades relacionadas con la conectividad del gráfico de complemento.