Geomancia
La geomancia es un método de adivinación que interpreta las marcas en el suelo o los patrones formados por puñados de tierra, rocas o arena arrojados. La forma más frecuente de geomancia adivinatoria implica la interpretación de una serie de 16 figuras formadas por un proceso aleatorio que implica la recursividad, seguido de su análisis, a menudo aumentado con interpretaciones astrológicas. Figuras como Ricardo II también pensaron que la geomancia era una disciplina mayor que incluía elementos de filosofía, ciencia y alquimia.
La geomancia era practicada por personas de todas las clases sociales. Fue una de las formas de adivinación más populares en toda África y Europa, particularmente durante la Edad Media y el Renacimiento, aunque en la magia renacentista, la geomancia se clasificaba como una de las siete "artes prohibidas", junto con la nigromancia., hidromancia, aeromancia, piromancia, quiromancia (quiromancia) y escapulimancia.
Historia
La palabra "geomancia", del griego tardío *γεωμαντεία *geōmanteía "adivinación de la tierra", se traduce literalmente como "adivinación de la tierra"; es una traducción en calco del término árabe ‛ilm al-raml, o la "ciencia de la arena". Versiones griegas anteriores de esta palabra tomaron prestada la palabra árabe raml ("arena") directamente, traduciéndola como rhamplion o rabolion. Otros nombres árabes para la geomancia incluyen khatt al-raml y darb al-raml.
Los nombres originales de las figuras en la geomancia del Medio Oriente se dieron tradicionalmente en árabe, excluyendo un origen persa. La referencia en los textos herméticos al mítico Ṭumṭum al-Hindi apunta potencialmente a un origen indio, aunque Stephen Skinner cree que esto es poco probable. Lo más probable es que tenga un origen islámico o árabe, ya que las amplias rutas comerciales de los comerciantes árabes facilitarían el intercambio de cultura y conocimiento.
Académicos y universidades europeos comenzaron a traducir textos y tratados árabes a principios de la Edad Media, incluidos los de geomancia. Isidoro de Sevilla (c. 560 - 636) enumera la geomancia con otros métodos de adivinación, incluida la piromancia, la hidromancia, la aeromancia y la nigromancia, sin describir su aplicación o métodos. Podría ser que Isidoro de Sevilla enumerara métodos de videncia elemental más allá de lo que comúnmente se conoce como geomancia. El poema Experimentarius atribuido a Bernardus Silvestris, que escribió a mediados del siglo XII, fue una traducción en verso de una obra sobre geomancia astrológica. Uno de los primeros discursos sobre geomancia traducido al latín fue el Ars Geomantiae de Hugo de Santalla (fl. principios del siglo XII). En este punto, la geomancia debe haber sido un sistema de adivinación establecido en las áreas de habla árabe de África y el Medio Oriente.
Otros traductores, como Gerardo de Cremona (c. 1114 – 1187), también produjeron nuevas traducciones sobre geomancia que incorporaron elementos y técnicas astrológicas que, hasta ese momento, eran, ignorado. A partir de este momento, más eruditos europeos estudiaron y aplicaron la geomancia, escribiendo muchos tratados en el proceso. Henry Cornelius Agrippa (1486–1535), Christopher Cattan (La Géomancie du Seigneur Christofe de Cattan (1558)) y John Heydon (1629 – c. 1667) produjo tratados sobre geomancia muy citados y bien estudiados, junto con otros filósofos, ocultistas y teólogos hasta el siglo XVII, cuando el interés por el ocultismo y la adivinación comenzó a disminuir debido al surgimiento de la Revolución Científica y la Era de la Ciencia. Razón.
La geomancia experimentó un renacimiento en el siglo XIX, cuando surgió un renovado interés por lo oculto debido a los trabajos de Robert Thomas Cross (1850–1923) y de Edward Bulwer-Lytton (1803–1873). Franz Hartmann publicó su texto, Los principios de la geomancia astrológica, (traducción al inglés: 1889) que estimuló un nuevo interés en el sistema de adivinación. Con base en este y algunos textos más antiguos, la Orden Hermética de la Golden Dawn (fundada en 1887) comenzó la tarea de recopilar conocimientos sobre geomancia junto con otros temas ocultos, con ellos, Aleister Crowley (1875-1947) publicó sus trabajos que integraban varios sistemas ocultos de conocimiento. Sin embargo, debido al poco tiempo que los miembros de Golden Dawn deseaban aprender, practicar y enseñar las antiguas artes ocultas, muchos sistemas elaborados de adivinación y rituales tuvieron que ser comprimidos, perdiendo mucho en el proceso. En efecto, habían reducido la geomancia de un arte complejo de interpretación y habilidad para reconocer patrones a buscar respuestas predefinidas basadas en pares de figuras.
Al igual que otros sistemas de adivinación, la geomancia tiene asociaciones mitológicas. Según un texto árabe hermético, Idris (o Hermes Trismegistus) fue testigo del ángel Jibril en un sueño. Idris pidió iluminación y Jibril procedió a dibujar una figura geomántica. Cuando se le preguntó qué estaba haciendo, Jibril instruyó a Idris en las artes geománticas. Manteniendo este secreto, buscó a Ṭumṭum al-Hindi, un rey indio, quien luego escribió un libro sobre geomancia. Este libro pasó de círculos clandestinos a manos de Khalaf al-Barbarĩ, quien viajó a Medina y fue convertido al Islam por el propio profeta Mahoma. Confesando conocer un arte adivinatorio, explicó que los profetas preislámicos conocían la geomancia, y que aprendiendo geomancia, uno puede "saber todo lo que sabía el profeta".
Otra historia mitológica sobre el origen de la geomancia también involucra a Idris. Después de orar a Dios para que le diera a Idris un medio fácil para ganarse la vida, Idris descansó un día, aburrido y sin trabajo, y comenzó a dibujar figuras ociosamente en la arena. Mientras lo hacía, un extraño apareció ante él y le preguntó qué estaba haciendo. Idris respondió que simplemente se estaba entreteniendo, pero el extraño respondió que estaba haciendo un acto muy serio. Idris se volvió incrédulo y trató de negar esto, pero el extraño le explicó el significado de la figura que dibujó Idris. Luego le ordenó a Idris que dibujara otra figura y, al hacerlo, el extraño explicó el significado y la importancia de esa figura.
La pareja continuó así hasta que Idris descubrió y entendió las dieciséis cifras. Luego, el extraño le enseñó a Idris cómo formar las figuras de manera regular y qué significaban los resultados, enseñándole cómo saber cosas que no se pueden saber solo con los sentidos físicos. Después de probar Idris' nuevos conocimientos y habilidades de geomancia, y revelándose como el ángel Jibril en el proceso, el extraño desapareció. Idris, agradecido a Dios y a Su mensajero por haber aprendido este arte, nunca se lo reveló a nadie. Antes de ser elevado a Dios, escribió un libro describiendo el arte como Jibril le había enseñado y de sus sucesores.
Otras tablillas y registros de la antigüedad identifican a Idris con los profetas Daniel o con Enoc. Esto se hizo para dar a la geomancia una posición legítima como don y habilidad de Dios, especialmente porque uno de los profetas la había practicado. Sin embargo, quienes argumentaron en contra de la geomancia, como Ibn Khaldun en su Muqaddima (1377), respondieron que se trataba de un sistema de conocimiento preislámico y que todas esas epistemologías quedaron obsoletas con la revelación de el Corán.
A lo largo de la evolución y migración de la geomancia, varios cuentos y obras de teatro incorporaron aspectos del arte en sus historias. En una historia de Las mil y una noches, tanto el mago africano como su hermano usan la geomancia para encontrar a Aladino y hacerle daño. La primera mención impresa de la geomancia se produjo en Piers Plowman de William Langland, donde se compara desfavorablemente con el nivel de experiencia que una persona necesita para la astronomía ("gemensye [geomesye] es gynful de speche"). En 1386, Chaucer usó el "Parson's Tale" para burlarse de la geomancia en Cuentos de Canterbury: "¿Qué decimos nosotros de los que creen en divynailes como... geomancia...? También se sabía que Shakespeare y Ben Jonson usaban la geomancia para el alivio cómico. La Divina Comedia de Dante Alighieri (principios del siglo XIV) hace una referencia pasajera a la geomancia. En las dos primeras estrofas del Canto XIX del Purgatorio,
Era la hora cuando el calor diurno
no más puede calentar la frialdad de la luna, vencido por la tierra, o por la peraventura Saturno,
Cuando geomanteles su Fortuna Major ver en el oriente antes del amanecer
levantarse por un camino que permanece largo no...
—Dante Aligheri, referencia a la Gran Fortuna (Fortuna Major) y el Camino ("el camino")
Generando las cartas geománticas
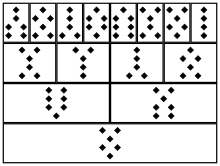
La geomancia requiere que el geomántico cree dieciséis líneas de puntos o marcas sin contar, creando dieciséis números aleatorios. Sin tomar nota del número de puntos logrados, el geomante proporciona el mecanismo aparentemente aleatorio necesario para la mayoría de las formas de adivinación. Una vez que se producen las líneas, el geomante marca los puntos de dos en dos hasta que uno o dos puntos quedan en la línea; matemáticamente, esto es lo mismo que producir dos puntos si el número es par o un punto si el número es impar. Tomando estos puntos sobrantes en grupos de cuatro, forman las primeras cuatro figuras geománticas y forman la base para la generación de las figuras restantes. Una vez hecho esto, el "inspirado" se realiza una parte de la lectura geomántica; lo que queda es el cálculo algorítmico.
Tradicionalmente, la geomancia requiere una superficie de arena y las manos o un palo, pero se puede hacer igualmente bien con una tableta de cera y un lápiz óptico o con un bolígrafo y papel; los objetos ritualizados pueden o no ser deseados para su uso en la adivinación. A menudo, al dibujar marcas o figuras, los geománticos procederán de derecha a izquierda como tradición de los orígenes árabes de la geomancia, aunque esto no es obligatorio. Los métodos modernos de geomancia incluyen, además de las formas tradicionales, generadores de números aleatorios computarizados u objetos arrojadizos; otros métodos, incluido contar los ojos en las papas. Algunos practicantes usan cartas especializadas, en las que cada carta representa una sola figura geomántica; en este caso, solo se extraen cuatro cartas después de barajar. También se han utilizado máquinas especializadas para generar cartas geománticas completas.
Las figuras se ingresan en una tabla especializada, conocida como tabla de escudos, que ilustra los procesos recursivos que recuerdan al conjunto de Cantor que forman las figuras. Las primeras cuatro figuras se denominan matres, o Madres, y forman la base para el resto de las figuras del cuadro; ocupan las primeras cuatro casas en la esquina superior derecha, de modo que la primera Madre está en el extremo derecho, la segunda Madre está en su izquierda, y así sucesivamente (continuando con la tradición de derecha a izquierda).
Las siguientes cuatro figuras, las filiae, o Hijas, se forman reorganizando las líneas utilizadas en las Madres: la primera Hija se forma tomando la primera línea de la primera, segunda, tercera, y cuarta Madres en orden y reorganizándolas para que sean la primera, segunda, tercera y cuarta línea de la primera Hija, respectivamente. El proceso se realiza de manera similar para la segunda Hija usando la segunda línea de las Madres, y así sucesivamente. Las Hijas se colocan en las próximas cuatro casas en orden en la misma fila que las Madres.
Después de formar los ocho matres y filiae, se forman los cuatro nepotes (o sobrinas) sumando aquellas parejas de figuras que descansan sobre las casas de las respectivas sobrinas. Por lo tanto, la primera y la segunda Madre se suman para formar la primera Sobrina, la tercera y la cuarta Madre se suman para formar la segunda Sobrina, y así sucesivamente. Aquí, la suma implica sumar los puntos en las respectivas líneas de los padres: si la suma es un número par, la línea de la figura resultante tendrá dos puntos, y si la suma es impar, la línea tendrá un punto.. Conceptualmente, este es el mismo procedimiento en lógica matemática que el exclusivo o, donde se usa una línea con dos puntos en lugar de "falso" y una línea con un punto en lugar de "verdadero".
De los cuatro nepotes, se forman los dos testículos (o Testigos) de la misma manera que los nepotes: el primero y el segundo Las sobrinas forman el Testigo derecho, y la tercera y cuarta sobrinas forman el Testigo izquierdo. De los Testigos, utilizando el mismo proceso de adición, se forma el iudex, o Juez. También se genera una decimosexta figura, la Reconciliadora o superiudex, al agregar el Juez y la Primera Madre, aunque esto se ha visto como extraño y una "figura de respaldo" en tiempos recientes.
Interpretación de los gráficos
Es muy probable que el gráfico del escudo haya proporcionado una guía visual temprana para generar las figuras, y la respuesta interpretada se centraría en las figuras decimoquinta y decimosexta, el juez y el reconciliador. Los geomantes expertos observan todo el gráfico, interpretando (entre otras cosas) los significados de las cifras según su ubicación en el gráfico, el significado numérico de los puntos totales y las similitudes producidas por las cifras añadidas. Generalmente, el Juez representa la respuesta a la pregunta, el Testigo Derecho describe el lado de la consulta del que consulta, el Testigo Izquierdo representa el lado de la pregunta y el Reconciliador representa el efecto del resultado (o Juez).) sobre el consultante. El geomante hábil puede deducir las causas fundamentales de la situación, las influencias ocultas, el resultado y sus consecuencias, y las tendencias y eventos generales en la vida del consultante a través de la interpretación del gráfico.
Una división de la tabla de escudos para la interpretación involucra trillizos de las figuras llamadas triplicidades. Cada triplicidad contiene dos de las Madres o dos de las Hijas y la Sobrina que de ellas resulta. Pueden interpretarse de manera similar a los Testigos y el Juez, en que el padre derecho representa el pasado, el hijo el presente y el padre izquierdo el futuro; otra forma de interpretar dicho triplete ve al padre derecho como el lado, los aliados, los recursos y las opiniones del consultante, el padre izquierdo como el lado cuestionado y el niño como la interacción de los dos lados.
| Triplicidad | Figures Involved | Interpretación |
|---|---|---|
| Primera Triplicidad | Primera Madre, Segunda Madre, Primera Niza | Salud, disposición, perspectivas y hábitos del aprendiz. Tendencias actuales en la vida del aprendiz. |
| Segunda Triplicidad | Tercera Madre, Cuarta Madre, Segunda Niza | Las influencias en la vida del aprendiz en el momento de la lectura. Factores que dan forma a la vida del aprendiz y a la situación que rodea a la consulta. |
| Tercera Triplicidad | Primera Hija, Segunda Hija, Tercera Niza | Los lugares más frecuentados por el aprendiz, incluyendo el hogar y el lugar de trabajo. Personas y objetos encontrados en esos lugares. Familia, parejas y compañeros de casa de los queren. |
| Cuarta Triplicidad | Tercera Hija, Cuarta Hija, Cuarta Niza | Amigos, asociados, colaboradores, compañeros de trabajo, colegas de los queren, así como personas en autoridad sobre el queren. Situaciones y factores causados por fuentes externas. |
Otro método para evaluar una carta geomántica consiste en tomar la suma total de todos los puntos de 16 cifras dentro de la carta de escudo. Para evaluar qué tan rápido se resolvería la situación cuestionada, Pietro d'Abano sugirió que la suma total se compare con la suma de todos los puntos en las dieciséis figuras geománticas, que es 96. Si la suma del gráfico es 96, entonces la resolución de la consulta será "rápida, y ni lenta ni dudosa;" es decir, que todo lo que pudiera actuarse en la situación descrita por la consulta se resolvería sin demora ni adelanto. Si la suma es inferior a 96, se resolverá rápidamente y en un grado proporcional a la diferencia entre 96 y el total. Por el contrario, si la suma es superior a 96, se resolverá lentamente.
Los geománticos europeos proporcionaron un método alternativo para interpretar las cifras a través del gráfico de casas, que presenta las doce casas astrológicas. Aquí, asignan las cifras del gráfico de escudos a las casas en el gráfico de casas; el orden utilizado difiere entre los diferentes círculos de ocultistas. Si bien los geomantes europeos todavía usaban la carta de escudos para generar las cifras y proporcionar la mayoría de las respuestas, aumentaron la geomancia con técnicas astrológicas en la carta de casas. Según la consulta, podrían proporcionar una visión más profunda de la vida del consultante, los factores que dan forma a la consulta en sí y el alcance de las situaciones involucradas. Tomaron nota cuando varias casas compartían la misma figura; como esta figura pasa de una casa a la siguiente, generalmente indica que la misma situación o evento afecta a cada una de esas casas.
Pietro d'Abano analiza los principales modos de perfección utilizados en las interpretaciones geománticas con significadores en su ensayo sobre geomancia. En la geomancia astrológica, los significadores se eligen en función de la identidad del consultante y la identidad del consultado. Generalmente, excepto cuando el consultante pregunta sobre una situación sobre un tema que no tiene una conexión inmediata consigo mismo, el significador del consultante se ubica en la primera casa (ver Casa Derivada).
El significador consultado se identifica según el enfoque de la consulta: esto se basa en la relación de la consulta con las casas astrológicas. Algunas preguntas requieren más de dos significadores, como en una consulta que involucra varios factores primarios (por ejemplo, dos partes que se pelean por una propiedad). Las consultas que tienen una respuesta de sí o no, o posible-imposible, pueden responderse fácilmente con estos modos de perfección. Si el gráfico es perfecto, la respuesta es "sí". De lo contrario, en el caso de negación de la perfección, "no".
También se debe considerar la naturaleza de las figuras en sí. Si un gráfico se perfecciona con cifras negativas, por ejemplo, el asunto se resolverá, pero es posible que al consultante no le guste el resultado. Por otro lado, si el gráfico no es perfecto pero las cifras son buenas, entonces el asunto no se resolverá aunque el consultante pueda arreglárselas sin él.
| Modo de perfección | Interacción de las cifras | Interpretación |
|---|---|---|
| Ocupación | El significado del querenista y el significado del quesitado son la misma figura. | Una conexión natural entre querent y quesited. El asunto resolverá por su propia naturaleza sin esfuerzo extra. |
| Conjunción | Uno de los significadores se mueve a una casa justo al lado de la casa del otro significador. | Los queren y quesited se encuentran. El significado que se mueve muestra qué partido debe trabajar para alcanzar la resolución: si el interlocutor se mueve a la de los quesiados, entonces el querer tendrá que trabajar para la resolución. De lo contrario, el quesitado resolverá las cosas sin necesidad del aprendiz. |
| Mutación | Los dos significadores aparecen al lado del otro en otro lugar del gráfico. | La resolución vendrá por alguna manera inesperada o inusual. Prueba nuevas avenidas que normalmente no se esperarían. |
| Traducción | La misma figura aparece en casas directamente al lado de las casas de los significadores. | La resolución llegará a través de un tercero. Un mediador ayudará a salvar la brecha entre el queren y el quesitado. |
| Denial | No existe conexión entre los dos significadores. | La falta de perfección en un gráfico. Los queren y los quesiados no pueden alcanzarse. Sin resolución. |
Además de los modos de perfección, los geomantes a menudo tomaban nota de los aspectos entre esas figuras que pasaban a otras casas, y especialmente aquellas que formaban aspectos con los significadores. A menudo, cuando una carta negaba la perfección, los geomantes observaban cómo los significadores se aspectaban entre sí; los aspectos aquí conservan significados similares de la astrología.
Christopher Cattan aboga por utilizar la fuerza de las casas astrológicas para determinar la resolución. Al observar la naturaleza de las figuras (buenas o malas, según la consulta) y en qué tipo de casa caen (angular, sucesiva o cadente), juzga el efecto total de las figuras en la consulta. Las figuras que caen en casas cadentes tienen poco o ningún efecto, las que caen en casas sucesivas tienen un efecto transitorio, y las que caen en casas angulares tienen el efecto más fuerte y duradero sobre la consulta.
Otros ejemplos de técnicas astrológicas utilizadas en la geomancia incluyen la asignación de regencias zodiacales a las figuras geománticas, la vinculación de figuras geománticas a partes del cuerpo según los regentes zodiacales y la asignación de espíritus, inteligencias y genios planetarios a las figuras según sus planetas regentes..
Geomancia y matemáticas
Los cuatro elementos binarios de cada figura permiten 16 combinaciones diferentes, cada una llamada cuadro. Como cada gráfico se genera a partir de las cuatro Madres, hay un número total de 164, o 65 536, gráficos posibles. Debido a las matemáticas de la tabla, solo las figuras que tienen un número par de puntos en total pueden convertirse en Jueces; cada uno de los ocho Jueces tiene entonces 8.192 cartas asociadas. Los practicantes tradicionales de la geomancia utilizan este conocimiento como un tipo de verificación de paridad en el gráfico para asegurarse de que no se hayan cometido errores al calcular las cifras.
En cada cuadro, si se observan las dieciséis figuras (las cuatro Madres, las cuatro Hijas, las cuatro Sobrinas, los Testigos, el Juez y la Reconciliadora), al menos dos de las figuras deben ser iguales. Como el Reconciliador generalmente se denomina una figura opcional, 16 combinaciones de figuras de la Madre pueden producir un gráfico en el que las Madres, las Hijas, las Sobrinas, los Testigos y el Juez son todos únicos.
Populus no puede aparecer en estos gráficos, ya que matemáticamente requiere que dos figuras sean iguales para formarse, o produce una figura duplicada cuando se agrega a otra figura. En tales cartas, el Juez será siempre uno de Conjunctio, Amissio, Carcer o Acquisitio. Las dieciséis combinaciones de Madres, en orden de la Primera a la Cuarta Madre, son
- Puer, Caput Draconis, Tristitia, Albus
- Conjunctio, Puella, Fortuna Major, Tristitia
- Puella, Puer, Tristitia, Albus
- Puella, Cauda Draconis, Tristitia, Albus
- Rubeus, Laetitia, Puella, Puer
- Rubeus, Laetitia, Cauda Draconis, Puella
- Rubeus, Laetitia, Cauda Draconis, Caput Draconis
- Rubeus, Laetitia, Caput Draconis, Puer
- Acquisitio, Puella, Albus, Fortuna Major
- Laetitia, Fortuna Minor, Puer, Conjunctio
- Laetitia, Fortuna Minor, Acquisitio, Cauda Draconis
- Cauda Draconis, Caput Draconis, Tristitia, Albus
- Caput Draconis, Amissio, Fortuna Major, Tristitia
- Caput Draconis, Carcer, Albus, Fortuna Major
- Fortuna Menor, Rubeus, Puer, Amissio
- Fortuna Menor, Rubeus, Carcer, Cauda Draconis
Otras formas de geomancia
La tradición árabe consiste en dibujar dieciséis líneas aleatorias de puntos en la arena. Este mismo proceso sobrevivió prácticamente sin cambios a través de su introducción en Europa en la era medieval, y sobrevive hasta el día de hoy en varios países árabes. Sikidy y otras formas de adivinación africana también siguen técnicas que se han mantenido prácticamente sin cambios.
En África, una forma tradicional de geomancia consiste en arrojar puñados de tierra al aire y observar cómo cae la tierra. También puede involucrar a un ratón como agente del espíritu de la tierra. Ifá, una de las formas más antiguas de geomancia, se originó en África occidental y utiliza las mismas dieciséis figuras geománticas que en la geomancia árabe y occidental con diferentes significados y nombres; el proceso se reduce a usar solo dos cifras. En China, el adivino puede entrar en trance y hacer marcas en el suelo que son interpretadas por un asociado (a menudo un niño pequeño o analfabeto). Formas similares de geomancia incluyen la adivinación que involucra los patrones que se ven en las rocas o el suelo.
La práctica de adivinación china del I Ching tiene varias similitudes sorprendentes con la geomancia. Incluye una serie de trigramas binarios (a diferencia de los tetragramas utilizados en geomancia) que se generan al azar, cuyas figuras resultantes se toman en combinación. Sin embargo, las figuras no se agregan ni se reorganizan como en la geomancia, sino que se toman para formar un solo hexagrama. Mientras que hay 23 u ocho trigramas, hay 26 o 64 hexagramas. Esto produce un conjunto más pequeño de gráficos resultantes que la geomancia.
Vastu shastra es un sistema arquitectónico tradicional de la India que literalmente se traduce como "ciencia de la arquitectura". Estos son textos que se encuentran en el subcontinente indio que describen los principios de diseño, distribución, medidas, preparación del suelo, disposición del espacio y geometría espacial. Vastu Shastras incorpora creencias hindúes tradicionales y, en algunos casos, budistas. Los diseños están destinados a integrar la arquitectura con la naturaleza, las funciones relativas de varias partes de la estructura y las antiguas creencias utilizando patrones geométricos (yantra), simetría y alineaciones direccionales.
Vastu Shastra son la parte textual de Vastu Vidya, siendo este último el conocimiento más amplio sobre arquitectura y teorías de diseño de la antigua India. El conocimiento de Vastu Vidya es una colección de ideas y conceptos, con o sin el apoyo de diagramas de diseño, que no son rígidos. Más bien, estas ideas y conceptos son modelos para la organización del espacio y la forma dentro de un edificio o colección de edificios, en función de sus funciones en relación con los demás, su uso y la estructura general del Vastu. Los principios antiguos de Vastu Shastra incluyen aquellos para el diseño de Mandir (templos hindúes) y los principios para el diseño y distribución de casas, pueblos, ciudades, jardines, caminos, obras hidráulicas, tiendas y otras áreas públicas..
Kumalak es un tipo de geomancia que se practica en Kazajstán, Tuva y otras partes de Asia Central. Kumalak hace uso de una cuadrícula de tres por tres, en la que un chamán colocará ritualmente hasta 41 cuentas. Estos chamanes usan kumalak más para conectarse con sus ancestros y guías espirituales que para obtener información a través de la adivinación. Además, los chamanes que usan kumalak deben ser iniciados y enseñados a realizar correctamente los rituales de kumalak. Según ellos, kumalak es un antiguo sistema de conocimiento que se remonta a las raíces de su civilización.
En Corea, esta tradición fue popularizada en el siglo IX por el monje budista Toson (Doseon). En Corea, la geomancia toma la forma de interpretar la topografía de la tierra para determinar eventos futuros o la fuerza de una dinastía o familia en particular. Por lo tanto, no solo eran importantes la ubicación y las formas del terreno, sino que la topografía podría cambiar y causar desagrado y la necesidad de reubicarse. La idea todavía se acepta en muchas sociedades del sudeste asiático en la actualidad, aunque con fuerza reducida.
En el siglo XIX, los misioneros cristianos en China tradujeron feng shui como "geomancia" debido a sus observaciones de los chamanes y sacerdotes locales que manipulan el flujo y la dirección de la energía en función de la estética, la ubicación y la posición de los objetos y edificios. Aunque proviene de una tradición distinta, el término "geomancia" ahora comúnmente incluye feng shui. De manera similar, la introducción de un sistema indio similar de estética y posicionamiento para armonizar las energías locales, vastu shastra, se conoce con el nombre de "geomancia". Debido a que la definición ha cambiado con el tiempo (junto con la definición reconocida del sufijo -mancy), "geomancy" puede abarcar cualquier práctica espiritual, metafísica o pseudocientífica que esté relacionada con la Tierra. En tiempos recientes, el término se ha aplicado a una amplia gama de otras actividades ocultas y marginales, incluidos los misterios de la Tierra y la introducción de líneas ley y Bau-Biologie.
En la literatura fantástica
En alguna literatura de fantasía, especialmente la que trata sobre los cuatro elementos griegos clásicos (aire, agua, fuego, tierra), la geomancia se refiere a la magia que controla la tierra (y, a veces, el metal y los cristales).
Contenido relacionado
La Última Cena (Leonardo)
Misión San Buenaventura
Críticas a los Testigos de Jehová