Función trigonométrica

Compartir Imprimir Citar

En matemáticas, las funciones trigonométricas (también llamadas funciones circulares, funciones angulares o funciones goniométricas) son funciones reales que relacionan un ángulo de un triángulo rectángulo con las proporciones de las longitudes de dos de sus lados. Son ampliamente utilizados en todas las ciencias que están relacionadas con la geometría, como la navegación, la mecánica de sólidos, la mecánica celeste, la geodesia y muchas otras. Se encuentran entre las funciones periódicas más simples y, como tales, también se utilizan ampliamente para estudiar fenómenos periódicos a través del análisis de Fourier.

Las funciones trigonométricas más utilizadas en las matemáticas modernas son: el seno, el coseno y la tangente. Sus recíprocos son respectivamente la cosecante, la secante y la cotangente, que se usan menos. Cada una de estas seis funciones trigonométricas tiene una función inversa correspondiente y un análogo entre las funciones hiperbólicas.

Seno
Coseno
Tangente
Cosecante
Secante
Cotangente

Las definiciones más antiguas de funciones trigonométricas, relacionadas con triángulos rectángulos, las definen solo para ángulos agudos. Para extender las funciones de seno y coseno a funciones cuyo dominio es toda la línea real, a menudo se usan definiciones geométricas que usan el círculo unitario estándar (es decir, un círculo con radio 1 unidad); entonces el dominio de las otras funciones es la línea real con algunos puntos aislados eliminados. Las definiciones modernas expresan funciones trigonométricas como series infinitas o como soluciones de ecuaciones diferenciales. Esto permite extender el dominio de las funciones seno y coseno a todo el plano complejo, y el dominio de las demás funciones trigonométricas al plano complejo eliminando algunos puntos aislados.

Geometría y función de las funciones de seno, coseno y cotangente

Notación

Tradicionalmente, una abreviatura de tres letras de su nombre se usa como símbolo para representar la función trigonométrica en fórmulas, a saber, "sen", "cos", "tan", "sec", "csc" y "cot" para seno, coseno, tangente, secante, cosecante y cotangente, respectivamente. (En cambio, la función cosecante puede abreviarse como "cosec" de cinco letras). Además, se usa notación funcional, como sin (x). Los paréntesis pueden omitirse cuando no pueda haber confusión; un ejemplo de un caso que requiere corchetes es:

${displaystyle sin x+y}$

Esta expresión es ambigua ya que puede interpretarse como:

${displaystyle sin(x)+y}$ o ${displaystyle sin(x+y).}$

A diferencia de la notación funcional general, un número entero positivo que aparece como un superíndice después del símbolo de la función no denota una potencia bajo la composición de la función sino una multiplicación iterada. Por ejemplo:

$sin ^{2}x$ y ${ estilo de visualización sin ^ {2} (x)}$ denotan:

${ estilo de visualización pecado (x) pecado (x),}$ no ${ estilo de visualización pecado ( pecado x).}$

Sin embargo, el exponente -1 es una notación alternativa para la correspondiente función trigonométrica inversa. Es decir:

${ estilo de visualización pecado ^ {-1} x}$ y $sen^{-1}(x)$ denotan:

${ estilo de visualización arcsen x,}$ (arcoseno).

En este contexto, se podría considerar que el exponente denota una función compuesta o iterada, ya que se puede considerar que una función inversa es la función iterada -1 veces. Sin embargo, la utilización de valores de superíndice para representar niveles de iteración distintos de -1 no parece ser de uso común.

Seno y coseno a lo largo de la circunferencia

HSD

Definiciones de triángulos rectángulos

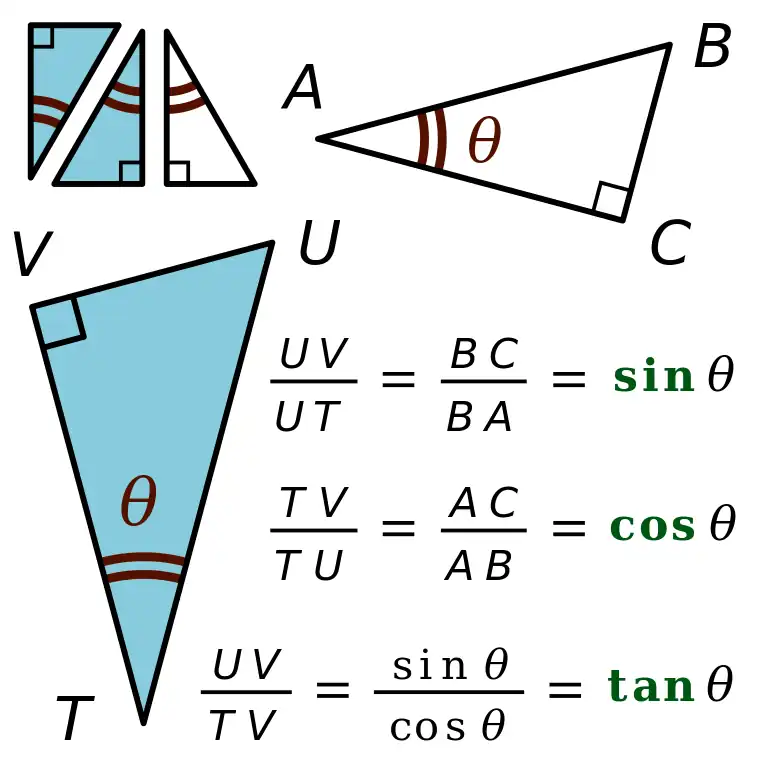
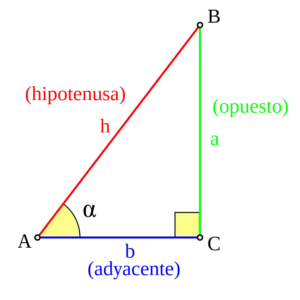
Si se da el ángulo agudo θ, entonces todos los triángulos rectángulos que tienen un ángulo de θ son similares entre sí. Esto significa que la razón de cualquiera de las longitudes de dos lados depende solo de θ. Así, estas seis razones definen seis funciones de θ, que son las funciones trigonométricas. En las siguientes definiciones, la hipotenusa es la longitud del lado opuesto al ángulo recto, opuesto representa el lado opuesto al ángulo dado θ y adyacente representa el lado entre el ángulo θ y el ángulo recto.

{displaystyle sin theta ={frac {mathrm {opuesto} }{mathrm {hipotenusa} }}}

{displaystyle csc theta ={frac {mathrm {hipotenusa} }{mathrm {opuesto} }}}

En un triángulo rectángulo, la suma de los dos ángulos agudos es un ángulo recto, es decir, 90° o π / 2 radianes. Por lo tanto y representan la misma razón, y por lo tanto son iguales. Esta identidad y relaciones análogas entre las otras funciones trigonométricas se resumen en la siguiente tabla. $pecado ( theta)$ ${displaystyle cos(90^{circ }-theta)}$

sin theta =cos left({frac {pi }{2}}-theta right)={frac {1}{csc theta }}

{displaystyle sin x=cos left(90^{circ }-xright)={frac {1}{csc x}}}

Función	Descripción	Relación
seno	opuesto / hipotenusa	$sin theta =cos left({frac {pi }{2}}-theta right)={frac {1}{csc theta }}$	${displaystyle sin x=cos left(90^{circ }-xright)={frac {1}{csc x}}}$
coseno	adyacente / hipotenusa	$cos theta =sin left({frac {pi }{2}}-theta right)={frac {1}{sec theta }},$	${displaystyle cos x=sin left(90^{circ }-xright)={frac {1}{sec x}},}$
tangente	opuesto / adyacente	$tan theta ={frac {sin theta }{cos theta }}=cot left({frac {pi }{2}}-theta right)={frac {1 {cottheta}}$	${displaystyle tan x={frac {sin x}{cos x}}=cot left(90^{circ }-xright)={frac {1}{cot x} }}$
cotangente	adyacente / opuesto	$cot theta ={frac {cos theta }{sin theta }}=tan left({frac {pi }{2}}-theta right)={frac {1 { bronceado theta}}$	${displaystyle cot x={frac {cos x}{sin x}}=tan left(90^{circ }-xright)={frac {1}{tan x} }}$
secante	hipotenusa / adyacente	$sec theta =csc left({frac {pi }{2}}-theta right)={frac {1}{cos theta }}$	${displaystyle sec x=csc left(90^{circ }-xright)={frac {1}{cos x}}}$
cosechar	hipotenusa / opuesto	$csc theta =sec left({frac {pi }{2}}-theta right)={frac {1}{sin theta }}$	${displaystyle csc x=sec left(90^{circ }-xright)={frac {1}{sin x}}}$

Radianes versus grados

En aplicaciones geométricas, el argumento de una función trigonométrica es generalmente la medida de un ángulo. Para este propósito, cualquier unidad angular es conveniente, y los ángulos se miden más comúnmente en unidades convencionales de grados en las que un ángulo recto es de 90° y una vuelta completa es de 360° (particularmente en matemáticas elementales).

Sin embargo, en cálculo y análisis matemático, las funciones trigonométricas generalmente se consideran de manera más abstracta como funciones de números reales o complejos, en lugar de ángulos. De hecho, las funciones sen y cos se pueden definir para todos los números complejos en términos de la función exponencial a través de series de potencias o como soluciones a ecuaciones diferenciales dados valores iniciales particulares (ver más abajo), sin referencia a ninguna noción geométrica. Las otras cuatro funciones trigonométricas (tan, cot, sec, csc) se pueden definir como cocientes y recíprocos de sen y cos, excepto cuando aparece cero en el denominador. Se puede probar, para argumentos reales, que estas definiciones coinciden con definiciones geométricas elementales si el argumento se considera como un ángulo dado en radianes. Además, estas definiciones dan como resultado expresiones simples para las derivadas e integrales indefinidas para las funciones trigonométricas. Por lo tanto, en entornos más allá de la geometría elemental, los radianes se consideran la unidad matemática natural para describir las medidas de los ángulos.

Cuando se emplean radianes (rad), el ángulo se da como la longitud del arco del círculo unitario subtendido por él: el ángulo que subtiende un arco de longitud 1 en el círculo unitario es 1 rad (≈ 57,3°), y un giro completo (360°) es un ángulo de 2 π (≈ 6,28) rad. Para el número real x, las notaciones sen x, cos x, etc. se refieren al valor de las funciones trigonométricas evaluadas en un ángulo de x rad. Si se trata de unidades de grados, el signo de grado debe mostrarse explícitamente (p. ej., sen x°, cos x°, etc.). Usando esta notación estándar, el argumento x para las funciones trigonométricas satisface la relación x = (180x / π)°, de modo que, por ejemplo, sen π = sen 180° cuando tomamos x = π. De esta forma, el símbolo de grado puede considerarse como una constante matemática tal que 1° = π /180 ≈ 0,0175.

Definiciones de círculo unitario

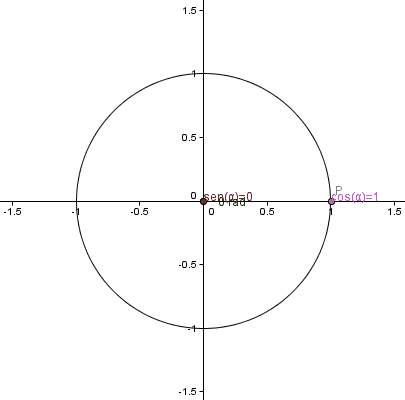
Las seis funciones trigonométricas se pueden definir como valores de coordenadas de puntos en el plano euclidiano que están relacionados con el círculo unitario, que es el círculo de radio uno centrado en el origen O de este sistema de coordenadas. Mientras que las definiciones de triángulos rectángulos permiten la definición de funciones trigonométricas para ángulos entre 0 y ${estilo de texto frac{pi}{2}}$ radianes (90°), las definiciones de círculo unitario permiten que el dominio de las funciones trigonométricas se extienda a todos los números reales positivos y negativos.

Sea $ma matemáticas L$ el rayo obtenido al girar en un ángulo θ la mitad positiva del eje x 0,}"> (rotación en sentido antihorario para y en sentido horario para <img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3da147239edfa6daac2c10f5258d18b41576d214" alt="{ estilo de visualización theta ). Este rayo interseca el círculo unitario en el punto ${displaystyle mathrm {A} =(x_{mathrm {A} },y_{mathrm {A} }).}$ El rayo ${displaystyle {mathcal {L}},}$ extendido a una línea si es necesario, interseca la línea de ecuación $x=1$ en el punto ${displaystyle mathrm {B} =(1,y_{mathrm {B} }),}$ y la línea de ecuación $y=1$ en el punto ${displaystyle mathrm {C} =(x_{mathrm {C} },1).}$ La línea tangente al círculo unitario en el punto A, es perpendicular ${displaystyle {mathcal {L}},}$ e interseca a la Los ejes y y x en los puntos ${displaystyle mathrm {D} =(0,y_{mathrm {D} })}$ y ${displaystyle mathrm {E} =(x_{mathrm {E} },0).}$ Las coordenadas de estos puntos dan los valores de todas las funciones trigonométricas para cualquier valor real arbitrario deθ de la siguiente manera.

Las funciones trigonométricas cos y sin se definen, respectivamente, como los valores de las coordenadas x e y del punto A. Es decir, ${displaystyle cos theta =x_{mathrm {A} }quad }$ y ${displaystyle quad sin theta =y_{mathrm {A} }.}$

En el rango $0 le theta le pi/2$ , esta definición coincide con la definición del triángulo rectángulo, tomando el triángulo rectángulo para tener la unidad de radio OA como hipotenusa. Y dado que la ecuación $x^{2}+y^{2}=1$ se cumple para todos los puntos ${ estilo de visualización mathrm {P} = (x, y)}$ del círculo unitario, esta definición de coseno y seno también satisface la identidad pitagórica. ${displaystyle cos ^{2}theta +sin ^{2}theta =1.}$

Las otras funciones trigonométricas se pueden encontrar a lo largo del círculo unitario como ${displaystyle tan theta =y_{mathrm {B} }quad }$ y ${displaystyle quad cot theta =x_{mathrm {C} },}$ ${displaystyle csc theta =y_{mathrm {D} }quad }$ y ${displaystyle quad sec theta =x_{mathrm {E} }.}$

Al aplicar los métodos de prueba geométrica y de identidad de Pitágoras, se puede demostrar fácilmente que estas definiciones coinciden con las definiciones de tangente, cotangente, secante y cosecante en términos de seno y coseno, es decir ${displaystyle tan theta ={frac {sin theta }{cos theta }},quad cot theta ={frac {cos theta }{sin theta }}, cuádruple sec theta ={frac {1}{cos theta }},quad csc theta ={frac {1}{sin theta }}.}$

Dado que la rotación de un ángulo de ${ estilo de visualización pm 2 pi}$ no cambia la posición o el tamaño de una forma, los puntos A, B, C, D y E son los mismos para dos ángulos cuya diferencia es un múltiplo entero de $2pi$ . Así, las funciones trigonométricas son funciones periódicas con período $2pi$ . Es decir, las igualdades ${displaystyle sin theta =sin left(theta +2kpi right)quad }$ y ${displaystyle quad cos theta =cos left(theta +2kpi right)}$

sostenga para cualquier ángulo θ y cualquier número entero k. Lo mismo es cierto para las otras cuatro funciones trigonométricas. Al observar el signo y la monotonicidad de las funciones seno, coseno, cosecante y secante en los cuatro cuadrantes, se puede demostrar que $2pi$ es el valor más pequeño para el cual son periódicas (es decir, $2pi$ es el período fundamental de estas funciones). Sin embargo, después de una rotación de un ángulo $Pi$ , los puntos B y C ya vuelven a su posición original, por lo que la función tangente y la función cotangente tienen un período fundamental de $Pi$ . Es decir, las igualdades ${displaystyle tan theta =tan(theta +kpi)quad }$ y ${displaystyle quad cot theta =cot(theta +kpi)}$

sostenga para cualquier ángulo θ y cualquier número entero k.

Valores algebraicos

Las expresiones algebraicas para los ángulos más importantes son las siguientes: ${displaystyle sin 0=sin 0^{circ }quad ={frac {sqrt {0}}{2}}=0}$ (ángulo cero) ${displaystyle sin {frac {pi }{6}}=sin 30^{circ }={frac {sqrt {1}}{2}}={frac {1}{2} }}$ ${displaystyle sin {frac {pi }{4}}=sin 45^{circ }={frac {sqrt {2}}{2}}={frac {1}{sqrt {2}}}}$ ${displaystyle sin {frac {pi }{3}}=sin 60^{circ }={frac {sqrt {3}}{2}}}$ ${displaystyle sin {frac {pi }{2}}=sin 90^{circ }={frac {sqrt {4}}{2}}=1}$ (ángulo recto)

Escribir los numeradores como raíces cuadradas de números enteros no negativos consecutivos, con un denominador de 2, brinda una manera fácil de recordar los valores.

Tales expresiones simples generalmente no existen para otros ángulos que son múltiplos racionales de un ángulo recto.

Para un ángulo que, medido en grados, es múltiplo de tres, los valores trigonométricos exactos del seno y el coseno pueden expresarse en términos de raíces cuadradas. Estos valores del seno y el coseno pueden así construirse con regla y compás.
Para un ángulo de un número entero de grados, el seno y el coseno se pueden expresar en términos de raíces cuadradas y la raíz cúbica de un número complejo no real. La teoría de Galois permite demostrar que, si el ángulo no es un múltiplo de 3°, las raíces cúbicas no reales son inevitables.
Para un ángulo que, expresado en grados, es un número racional, el seno y el coseno son números algebraicos, que pueden expresarse en términos de raíces enésimas. Esto resulta del hecho de que los grupos de Galois de los polinomios ciclotómicos son cíclicos.
Para un ángulo que, expresado en grados, no es un número racional, entonces tanto el ángulo como el seno y el coseno son números trascendentales. Este es un corolario del teorema de Baker, demostrado en 1966.

Valores algebraicos simples

La siguiente tabla enumera los senos, cosenos y tangentes de múltiplos de 15 grados de 0 a 90 grados.

θ en radianes	θ en grados	$pecado ( theta)$	$cos(theta)$	$bronceado ( theta)$
${ estilo de visualización 0}$	$0^{círculo}$	${ estilo de visualización 0}$	$1$	${ estilo de visualización 0}$
${ estilo de visualización { frac { pi} {12}}}$	${ estilo de visualización 15 ^ { círculo}}$	${frac {{raíz cuadrada {6}}-{raíz cuadrada {2}}}{4}}$	${frac {{raíz cuadrada {6}}+{raíz cuadrada {2}}}{4}}$	$2-{ sqrt {3}}$
$frac{pi}{6}$	$30^{círculo}$	${ fracción {1}{2}}$	${frac{sqrt {3}}{2}}$	${frac {sqrt {3}}{3}}$
$frac{pi}{4}$	$45^circ$	${frac {sqrt {2}}{2}}$	${frac {sqrt {2}}{2}}$	$1$
${ frac { pi }{3}}$	$60^{círculo}$	${frac{sqrt {3}}{2}}$	${ fracción {1}{2}}$	${ sqrt {3}}$
${ estilo de visualización { frac {5 pi} {12}}}$	${displaystyle 75^{circ}}$	${frac {{raíz cuadrada {6}}+{raíz cuadrada {2}}}{4}}$	${frac {{raíz cuadrada {6}}-{raíz cuadrada {2}}}{4}}$	${ estilo de visualización 2+ { sqrt {3}}}$
${ frac { pi }{2}}$	$90^{círculo}$	$1$	${ estilo de visualización 0}$	indefinido

En calculo

La tendencia moderna en matemáticas es construir geometría a partir del cálculo en lugar de lo contrario. Por lo tanto, excepto en un nivel muy elemental, las funciones trigonométricas se definen utilizando los métodos del cálculo.

Las funciones trigonométricas son diferenciables y analíticas en todos los puntos donde se definen; es decir, en todas partes para el seno y el coseno y, para la tangente, en todas partes excepto en π /2 + k π para todo entero k.

Las funciones trigonométricas son funciones periódicas, y su período primitivo es 2 π para el seno y el coseno, y π para la tangente, que es creciente en cada intervalo abierto (π /2 + k π, π /2 + (k + 1) π). En cada punto final de estos intervalos, la función tangente tiene una asíntota vertical.

En cálculo, hay dos definiciones equivalentes de funciones trigonométricas, ya sea utilizando series de potencias o ecuaciones diferenciales. Estas definiciones son equivalentes, ya que a partir de una de ellas es fácil recuperar la otra como propiedad. Sin embargo, la definición a través de ecuaciones diferenciales es algo más natural, ya que, por ejemplo, la elección de los coeficientes de la serie de potencias puede parecer bastante arbitraria, y la identidad pitagórica es mucho más fácil de deducir a partir de las ecuaciones diferenciales.

Definición por ecuaciones diferenciales

El seno y el coseno se pueden definir como la única solución al problema de valor inicial: ${displaystyle {frac {d}{dx}}sin x=cos x, {frac {d}{dx}}cos x=-sin x, sin(0)=0, \cos(0)=1.}$

Derivando de nuevo, ${textstyle {frac {d^{2}}{dx^{2}}}sin x={frac {d}{dx}}cos x=-sin x}$ y ${textstyle {frac {d^{2}}{dx^{2}}}cos x=-{frac {d}{dx}}sin x=-cos x}$ , por lo que tanto el seno como el coseno son soluciones de la ecuación diferencial ordinaria ${displaystyle y''+y=0.}$

Aplicando la regla del cociente a la tangente ${displaystyle tan x=sin x/cos x}$ , se deriva ${displaystyle {frac {d}{dx}}tan x={frac {cos ^{2}x+sin ^{2}x}{cos ^{2}x}}=1+ bronceado ^{2}x.}$

Expansión de la serie de potencia

Aplicando las ecuaciones diferenciales a series de potencias con coeficientes indeterminados, se pueden deducir relaciones de recurrencia para los coeficientes de la serie de Taylor de las funciones seno y coseno. Estas relaciones de recurrencia son fáciles de resolver y dan desarrollos a la serie ${displaystyle {begin{alineado}sen x&=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots \[6mu]&=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\[8pt]cos x&=1-{frac {x^{2}}{2!}}+{frac {x^{4} {4!}}-{frac {x^{6}}{6!}}+cdots \[6mu]&=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}x^{2n}.end{alineado}}}$

El radio de convergencia de estas series es infinito. Por lo tanto, el seno y el coseno se pueden extender a funciones completas (también llamadas "seno" y "coseno"), que son (por definición) funciones de valores complejos que están definidas y son holomorfas en todo el plano complejo.

Al estar definidas como fracciones de funciones enteras, las demás funciones trigonométricas pueden extenderse a funciones meromórficas, es decir funciones que son holomorfas en todo el plano complejo, excepto en algunos puntos aislados llamados polos. Aquí, los polos son los números de la forma ${estilo de texto (2k+1){frac {pi }{2}}}$ para la tangente y la secante, o ${ estilo de visualización k pi}$ para la cotangente y la cosecante, donde k es un número entero arbitrario.

Las relaciones de recurrencia también se pueden calcular para los coeficientes de la serie de Taylor de las otras funciones trigonométricas. Estas series tienen un radio de convergencia finito. Sus coeficientes tienen una interpretación combinatoria: enumeran permutaciones alternas de conjuntos finitos.

Más precisamente, definirU _n, el n ésimo número arriba/abajo,B _n, el n ésimo número de Bernoulli, yE _n, es el n ésimo número de Euler,

uno tiene las siguientes expansiones de serie:

Expansión de fracciones continuas

Las siguientes expansiones son válidas en todo el plano complejo: ${displaystyle sin x={cfrac {x}{1+{cfrac {x^{2}}{2cdot 3-x^{2}+{cfrac {2cdot 3x^{2} {4cdot 5-x^{2}+{cfrac {4cdot 5x^{2}}{6cdot 7-x^{2}+ddots }}}}}}}}}$ ${displaystyle cos x={cfrac {1}{1+{cfrac {x^{2}}{1cdot 2-x^{2}+{cfrac {1cdot 2x^{2} {3cdot 4-x^{2}+{cfrac {3cdot 4x^{2}}{5cdot 6-x^{2}+ddots }}}}}}}}}$ ${displaystyle tan x={cfrac {x}{1-{cfrac {x^{2}}{3-{cfrac {x^{2}}{5-{cfrac {x^{2 }}{7-ddots }}}}}}}}={cfrac {1}{{cfrac {1}{x}}-{cfrac {1}{{cfrac {3}{x} }-{cfrac {1}{{cfrac {5}{x}}-{cfrac {1}{{cfrac {7}{x}}-ddots }}}}}}}}}$

El último se utilizó en la histórica primera prueba de que π es irracional.

Expansión en fracciones parciales

Hay una representación en serie como expansión en fracciones parciales donde se resumen las funciones recíprocas recién traducidas, de modo que los polos de la función cotangente y las funciones recíprocas coinciden: ${displaystyle pi cot pi x=lim _{Nto infty}sum _{n=-N}^{N}{frac {1}{x+n}}.}$

Esta identidad se puede probar con el truco de Herglotz. Combinando el (– n) th con el n th término se obtiene una serie absolutamente convergente: ${displaystyle pi cot pi x={frac {1}{x}}+2xsum _{n=1}^{infty }{frac {1}{x^{2}-n ^{2}}}.}$

De manera similar, uno puede encontrar una expansión en fracciones parciales para las funciones secante, cosecante y tangente: ${displaystyle pi csc pi x=sum _{n=-infty }^{infty }{frac {(-1)^{n}}{x+n}}={frac { 1}{x}}+2xsum _{n=1}^{infty }{frac {(-1)^{n}}{x^{2}-n^{2}}},}$ ${displaystyle pi ^{2}csc ^{2}pi x=sum _{n=-infty }^{infty }{frac {1}{(x+n)^{2} }},}$ ${displaystyle pi sec pi x=sum _{n=0}^{infty}(-1)^{n}{frac {(2n+1)}{(n+{tfrac {1 {2}})^{2}-x^{2}}},}$ ${displaystyle pi tan pi x=2xsum _{n=0}^{infty}{frac {1}{(n+{tfrac {1}{2}})^{2}- x^{2}}}.}$

Expansión infinita de productos

El siguiente producto infinito por el seno es de gran importancia en el análisis complejo: ${displaystyle sin z=zprod _{n=1}^{infty}left(1-{frac {z^{2}}{n^{2}pi ^{2}}} right),quad zin mathbb {C}.}$

Para la demostración de esta expansión, véase Sine. De esto se puede deducir que ${displaystyle cos z=prod _{n=1}^{infty}left(1-{frac {z^{2}}{(n-1/2)^{2}pi ^ {2}}}right),quad zin mathbb {C}.}$

Relación con la función exponencial (fórmula de Euler)

La fórmula de Euler relaciona el seno y el coseno con la función exponencial: ${displaystyle e^{ix}=cos x+isin x.}$

Esta fórmula se considera comúnmente para valores reales de x, pero sigue siendo válida para todos los valores complejos.

Prueba: Sea ${displaystyle f_{1}(x)=cos x+isin x,}$ y ${displaystyle f_{2}(x)=e^{ix}.}$ Uno tiene ${displaystyle df_{j}(x)/dx=if_{j}(x)}$ para j = 1, 2. La regla del cociente implica así que ${displaystyle d/dx,(f_{1}(x)/f_{2}(x))=0}$ . Por lo tanto, ${displaystyle f_{1}(x)/f_{2}(x)}$ es una función constante, que es igual a1, ya que ${ estilo de visualización f_ {1} (0) = f_ {2} (0) = 1.}$ Esto prueba la fórmula.

Uno tiene ${displaystyle {begin{alineado}e^{ix}&=cos x+isin x\[5pt]e^{-ix}&=cos xisin x.end{alineado}} }$

Resolviendo este sistema lineal en seno y coseno, se pueden expresar en términos de la función exponencial: ${displaystyle {begin{alineado}sin x&={frac {e^{ix}-e^{-ix}}{2i}}\[5pt]cos x&={frac {e^{ ix}+e^{-ix}}{2}}.end{alineado}}}$

Cuando x es real, esto se puede reescribir como ${displaystyle cos x=operatorname {Re} left(e^{ix}right),qquad sin x=operatorname {Im} left(e^{ix}right).}$

La mayoría de las identidades trigonométricas se pueden probar expresando funciones trigonométricas en términos de la función exponencial compleja usando las fórmulas anteriores y luego usando la identidad ${displaystyle e^{a+b}=e^{a}e^{b}}$ para simplificar el resultado.

Definiciones usando ecuaciones funcionales

También se pueden definir las funciones trigonométricas usando varias ecuaciones funcionales.

Por ejemplo, el seno y el coseno forman el único par de funciones continuas que satisfacen la fórmula de diferencia $cos(x-y)=cos xcos y+sin xsin y,$

y la condición añadida<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/63db02f4b47b708e01b5392e6668ddb7efc1ce72" alt="{displaystyle 0<xcos x<sin x<xquad {text{ para }}quad 0<x

En el plano complejo

El seno y el coseno de un número complejo $z=x+iy$ se pueden expresar en términos de senos, cosenos y funciones hiperbólicas reales de la siguiente manera: ${displaystyle {begin{alineado}sin z&=sin xcosh y+icos xsinh y\[5pt]cos z&=cos xcosh yisin xsinh yend {alineado}}}$

Al aprovechar la coloración del dominio, es posible graficar las funciones trigonométricas como funciones de valores complejos. En el gráfico se pueden ver varias características exclusivas de las funciones complejas; por ejemplo, se puede ver que las funciones seno y coseno no están acotadas a medida que la parte imaginaria de $z$ se vuelve más grande (ya que el color blanco representa el infinito), y el hecho de que las funciones contienen ceros o polos simples es evidente por el hecho de que los ciclos de matiz alrededor de cada cero o polo exactamente una vez. La comparación de estos gráficos con los de las funciones hiperbólicas correspondientes resalta las relaciones entre los dos.

Identidades basicas

Muchas identidades interrelacionan las funciones trigonométricas. Esta sección contiene los más básicos; para obtener más identidades, consulte Lista de identidades trigonométricas. Estas identidades pueden probarse geométricamente a partir de las definiciones del círculo unitario o las definiciones del triángulo rectángulo (aunque, para las últimas definiciones, se debe tener cuidado con los ángulos que no están en el intervalo [0, π /2], ver Pruebas de identidades trigonométricas). Para pruebas no geométricas que usan solo herramientas de cálculo, se pueden usar directamente las ecuaciones diferenciales, de una manera similar a la de la prueba anterior de la identidad de Euler. También se puede usar la identidad de Euler para expresar todas las funciones trigonométricas en términos de exponenciales complejas y usar las propiedades de la función exponencial.

Paridad

El coseno y la secante son funciones pares; las otras funciones trigonométricas son funciones impares. Es decir: ${displaystyle {begin{alineado}sin(-x)&=-sin x\cos(-x)&=cos x\tan(-x)&=-tan x\ cot(-x)&=-cot x\csc(-x)&=-csc x\sec(-x)&=sec x.end{alineado}}}$

Períodos

Todas las funciones trigonométricas son funciones periódicas de período 2 π. Este es el período más pequeño, a excepción de la tangente y la cotangente, que tienen π como período más pequeño. Esto significa que, para cada entero k, se tiene ${displaystyle {begin{alineado}sin(x+2kpi)&=sin x\cos(x+2kpi)&=cos x\tan(x+kpi) &=tan x\cot(x+kpi)&=cot x\csc(x+2kpi)&=csc x\sec(x+2kpi)&= sec x.end{alineado}}}$

Identidad pitagórica

La identidad de Pitágoras, es la expresión del teorema de Pitágoras en términos de funciones trigonométricas. Está ${ estilo de visualización pecado ^ {2} x + cos ^ {2} x = 1.}$

Fórmulas de suma y diferencia

Las fórmulas de suma y diferencia permiten expandir el seno, el coseno y la tangente de una suma o diferencia de dos ángulos en términos de senos y cosenos y tangentes de los propios ángulos. Estos se pueden derivar geométricamente, utilizando argumentos que datan de Ptolomeo. También se pueden producir algebraicamente usando la fórmula de Euler.Suma ${displaystyle {begin{aligned}sin left(x+yright)&=sin xcos y+cos xsin y,\[5mu]cos left(x+yright)&=cos xcos y-sin xsin y,\[5mu]tan(x+y)&={frac {tan x+tan y}{1-tan xtan y}}.end{aligned}}}$ Diferencia ${displaystyle {begin{aligned}sin left(x-yright)&=sin xcos y-cos xsin y,\[5mu]cos left(x-yright)&=cos xcos y+sin xsin y,\[5mu]tan(x-y)&={frac {tan x-tan y}{1+tan xtan y}}.end{aligned}}}$

Cuando los dos ángulos son iguales, las fórmulas de suma se reducen a ecuaciones más simples conocidas como fórmulas de doble ángulo. ${displaystyle {begin{alineado}sin 2x&=2sin xcos x={frac {2tan x}{1+tan ^{2}x}},\[5mu]cos 2x&=cos ^{2}x-sin ^{2}x=2cos ^{2}x-1=1-2sin ^{2}x={frac {1-tan ^{ 2}x}{1+tan ^{2}x}},\[5mu]tan 2x&={frac {2tan x}{1-tan ^{2}x}}.end {alineado}}}$

Estas identidades se pueden utilizar para derivar las identidades de producto a suma.

Al establecer ${displaystyle t=tan {tfrac {1}{2}}theta,}$ todas las funciones trigonométricas de $theta$ se pueden expresar como fracciones racionales de $t$ : ${displaystyle {begin{alineado}sin theta &={frac {2t}{1+t^{2}}},\[5mu]cos theta &={frac {1-t ^{2}}{1+t^{2}}},\[5mu]tan theta &={frac {2t}{1-t^{2}}}.end{alineado}} }$

Juntos con ${displaystyle dtheta ={frac {2}{1+t^{2}}},dt,}$

esta es la sustitución del medio ángulo tangente, que reduce el cálculo de integrales y antiderivadas de funciones trigonométricas al de fracciones racionales.

Derivadas y antiderivadas

Las derivadas de funciones trigonométricas resultan de las de seno y coseno aplicando la regla del cociente. Los valores dados para las antiderivadas en la siguiente tabla se pueden verificar al diferenciarlas. El número C es una constante de integración.

$f(x)$	$f'(x)$	${ estilo de texto int f (x) , dx}$
$sin x$	$cos x$	${displaystyle -cos x+C}$
$cos x$	${ estilo de visualización - sen x}$	${ estilo de visualización sen x + C}$
${ estilo de visualización bronceado x}$	${displaystyle sec^{2}x=1+tan^{2}x}$	${displaystyle -ln left\|cos xright\|+C}$
${ estilo de visualización csc x}$	${ estilo de visualización - csc x cot x}$	${displaystyle -ln left\|csc x+cot xright\|+C}$
${ estilo de visualización sec x}$	${ estilo de visualización sec x bronceado x}$	${displaystyle ln left\|sec x+tan xright\|+C}$
${ estilo de visualización cuna x}$	${displaystyle -csc^{2}x=-1-cot^{2}x}$	${displaystyle ln left\|sin xright\|+C}$

Alternativamente, las derivadas de las 'cofunciones' se pueden obtener usando identidades trigonométricas y la regla de la cadena: ${displaystyle {begin{alineado}{frac {dcos x}{dx}}&={frac {d}{dx}}sin(pi /2-x)=-cos( pi /2-x)=-sen x,,\{frac {dcsc x}{dx}}&={frac {d}{dx}}sec(pi /2-x)=-sec(pi /2-x)tan(pi /2-x)=-csc xcot x,,\{frac {dcot x}{dx}}& ={frac {d}{dx}}tan(pi /2-x)=-sec ^{2}(pi /2-x)=-csc ^{2}x,. fin{alineado}}}$

Funciones inversas

Las funciones trigonométricas son periódicas y, por lo tanto, no inyectivas, por lo que estrictamente hablando, no tienen una función inversa. Sin embargo, en cada intervalo en el que una función trigonométrica es monótona, se puede definir una función inversa, y esto define las funciones trigonométricas inversas como funciones multivaluadas. Para definir una función inversa verdadera, se debe restringir el dominio a un intervalo donde la función es monótona y, por lo tanto, es biyectiva desde este intervalo a su imagen por la función. La elección común para este intervalo, llamado conjunto de valores principales, se da en la siguiente tabla. Como de costumbre, las funciones trigonométricas inversas se denotan con el prefijo "arco" antes del nombre o la abreviatura de la función.

Función	Definición	Dominio	Conjunto de valores principales
${displaystyle y=arcsen x}$	${displaystyle sin y=x}$	${ estilo de visualización -1 leq x leq 1}$	${textstyle -{frac {pi }{2}}leq yleq {frac {pi }{2}}}$
${displaystyle y=arccos x}$	${displaystyle cos y=x}$	${ estilo de visualización -1 leq x leq 1}$	${ estilo de texto 0 leq y leq pi }$
${displaystyle y=arctan x}$	${displaystyle tan y=x}$
${displaystyle y=operatorname {arccot} x}$	${displaystyle cot y=x}$
${displaystyle y=operatorname {arcsec} x}$	${ estilo de visualización seg y = x}$		${textstyle 0leq yleq pi,;yneq {frac {pi }{2}}}$
${displaystyle y=operatorname {arccsc} x}$	${ estilo de visualización csc y = x}$

Las notaciones sen, cos, etc. se usan a menudo para arcsen y arccos, etc. Cuando se usa esta notación, las funciones inversas pueden confundirse con inversas multiplicativas. La notación con el prefijo "arco" evita tal confusión, aunque "arcosegundo" para arcosecante puede confundirse con "arcosegundo".

Al igual que el seno y el coseno, las funciones trigonométricas inversas también se pueden expresar en términos de series infinitas. También se pueden expresar en términos de logaritmos complejos.

Aplicaciones

Ángulos y lados de un triángulo

En esta sección A, B, C denotan los tres ángulos (interiores) de un triángulo, y a, b, c denotan las longitudes de los respectivos bordes opuestos. Están relacionados por varias fórmulas, que son nombradas por las funciones trigonométricas que involucran.

Ley de los senos

La ley de los senos establece que para un triángulo arbitrario con lados a, b, y c y ángulos opuestos a esos lados A, B y C:

{displaystyle {frac {sin A}{a}}={frac {sin B}{b}}={frac {sin C}{c}}={frac {2Delta} {a B C}},}

donde Δ es el área del triángulo o, de manera equivalente,

{displaystyle {frac {a}{sin A}}={frac {b}{sin B}}={frac {c}{sin C}}=2R,}

donde R es el circunradio del triángulo.

Se puede probar dividiendo el triángulo en dos rectángulos y usando la definición anterior de seno. La ley de los senos es útil para calcular las longitudes de los lados desconocidos de un triángulo si se conocen dos ángulos y un lado. Esta es una situación común que ocurre en la triangulación, una técnica para determinar distancias desconocidas midiendo dos ángulos y una distancia cerrada accesible.

Ley de los cosenos

La ley de los cosenos (también conocida como fórmula del coseno o regla del coseno) es una extensión del teorema de Pitágoras:

{displaystyle c^{2}=a^{2}+b^{2}-2abcos C,}

o equivalente,

{displaystyle cos C={frac {a^{2}+b^{2}-c^{2}}{2ab}}.}

En esta fórmula, el ángulo en C es opuesto al lado c. Este teorema se puede probar dividiendo el triángulo en dos rectángulos y usando el teorema de Pitágoras.

La ley de los cosenos se puede usar para determinar un lado de un triángulo si se conocen dos lados y el ángulo entre ellos. También se puede usar para encontrar los cosenos de un ángulo (y, en consecuencia, los ángulos mismos) si se conocen las longitudes de todos los lados.

Ley de las tangentes

La ley de las tangentes dice que: ${displaystyle {frac {tan {frac {AB}{2}}}{tan {frac {A+B}{2}}}}={frac {ab}{a+b}} }$ .

Ley de las cotangentes

Si s es el semiperímetro del triángulo, (a + b + c)/2, y r es el radio de la circunferencia inscrita del triángulo, entonces rs es el área del triángulo. Por lo tanto, la fórmula de Heron implica que: ${displaystyle r={sqrt {{frac {1}{s}}(sa)(sb)(sc)}}}$ .

La ley de las cotangentes dice que: ${displaystyle cot {frac {A}{2}}={frac {sa}{r}}}$

Resulta que ${displaystyle {frac {cot {dfrac {A}{2}}}{sa}}={frac {cot {dfrac {B}{2}}}{sb}}={frac {cot {dfrac {C}{2}}}{sc}}={frac {1}{r}}.}$

Funciones periódicas

Las funciones trigonométricas también son importantes en física. Las funciones seno y coseno, por ejemplo, se utilizan para describir el movimiento armónico simple, que modela muchos fenómenos naturales, como el movimiento de una masa unida a un resorte y, para ángulos pequeños, el movimiento pendular de una masa que cuelga de un resorte. cuerda. Las funciones seno y coseno son proyecciones unidimensionales de movimiento circular uniforme.

Las funciones trigonométricas también resultan útiles en el estudio de funciones periódicas generales. Los patrones de onda característicos de las funciones periódicas son útiles para modelar fenómenos recurrentes como el sonido o las ondas de luz.

En condiciones bastante generales, una función periódica f (x) se puede expresar como una suma de ondas sinusoidales o cosenoidales en una serie de Fourier. Denotando las funciones base seno o coseno por φ _k, la expansión de la función periódica f (t) toma la forma:

{displaystyle f(t)=sum_{k=1}^{infty}c_{k}varphi_{k}(t).}

Por ejemplo, la onda cuadrada se puede escribir como la serie de Fourier

{displaystyle f_{text{cuadrado}}(t)={frac {4}{pi }}sum _{k=1}^{infty }{sin {big (}(2k- 1)t{grande)} sobre 2k-1}.}

En la animación de una onda cuadrada en la parte superior derecha se puede ver que unos pocos términos ya producen una aproximación bastante buena. A continuación se muestra la superposición de varios términos en la expansión de una onda de diente de sierra.

Historia

Si bien el estudio temprano de la trigonometría se remonta a la antigüedad, las funciones trigonométricas, tal como se usan hoy en día, se desarrollaron en el período medieval. La función de cuerda fue descubierta por Hiparco de Nicea (180-125 a. C.) y Ptolomeo del Egipto romano (90-165 d. C.). Las funciones de seno y verseno (1 – coseno) se remontan a las funciones jyā y koti-jyā utilizadas en la astronomía india del período Gupta (Aryabhatiya, Surya Siddhanta), a través de la traducción del sánscrito al árabe y luego del árabe al latín. (Consulte la tabla de senos de Aryabhata).

Las seis funciones trigonométricas en uso actual se conocían en las matemáticas islámicas en el siglo IX, al igual que la ley de los senos, utilizada para resolver triángulos. Con la excepción del seno (que fue adoptado de las matemáticas indias), los matemáticos persas y árabes descubrieron las otras cinco funciones trigonométricas modernas, incluyendo el coseno, la tangente, la cotangente, la secante y la cosecante. Al-Khwārizmī (c. 780–850) produjo tablas de senos, cosenos y tangentes. Alrededor del año 830, Habash al-Hasib al-Marwazi descubrió la cotangente y produjo tablas de tangentes y cotangentes. Muhammad ibn Jābir al-Harrānī al-Battānī (853–929) descubrió las funciones recíprocas de secante y cosecante, y produjo la primera tabla de cosecantes para cada grado de 1° a 90°.Las funciones trigonométricas fueron estudiadas más tarde por matemáticos como Omar Khayyám, Bhāskara II, Nasir al-Din al-Tusi, Jamshīd al-Kāshī (siglo XIV), Ulugh Beg (siglo XIV), Regiomontanus (1464), Rheticus y el estudiante de Rheticus. Valentino Otón.

Madhava de Sangamagrama (c. 1400) hizo avances tempranos en el análisis de funciones trigonométricas en términos de series infinitas. (Consulte la serie de Madhava y la tabla de senos de Madhava).

Los términos tangente y secante fueron introducidos por primera vez por el matemático danés Thomas Fincke en su libro Geometria rotundi (1583).

El matemático francés del siglo XVII Albert Girard hizo el primer uso publicado de las abreviaturas sin, cos y tan en su libro Trigonométrie.

En un artículo publicado en 1682, Leibniz demostró que sen x no es una función algebraica de x. Aunque introducidos como proporciones de los lados de un triángulo rectángulo, y por lo tanto parecen ser funciones racionales, el resultado de Leibnitz estableció que en realidad son funciones trascendentales de su argumento. La tarea de asimilar funciones circulares en expresiones algebraicas fue realizada por Euler en su Introducción al Análisis del Infinito (1748). Su método consistía en demostrar que las funciones seno y coseno son series alternas formadas a partir de los términos pares e impares, respectivamente, de la serie exponencial. Presentó la "fórmula de Euler", así como abreviaturas casi modernas (sin., cos.,Espiga. , cuna. , seg. , y cosec. ).

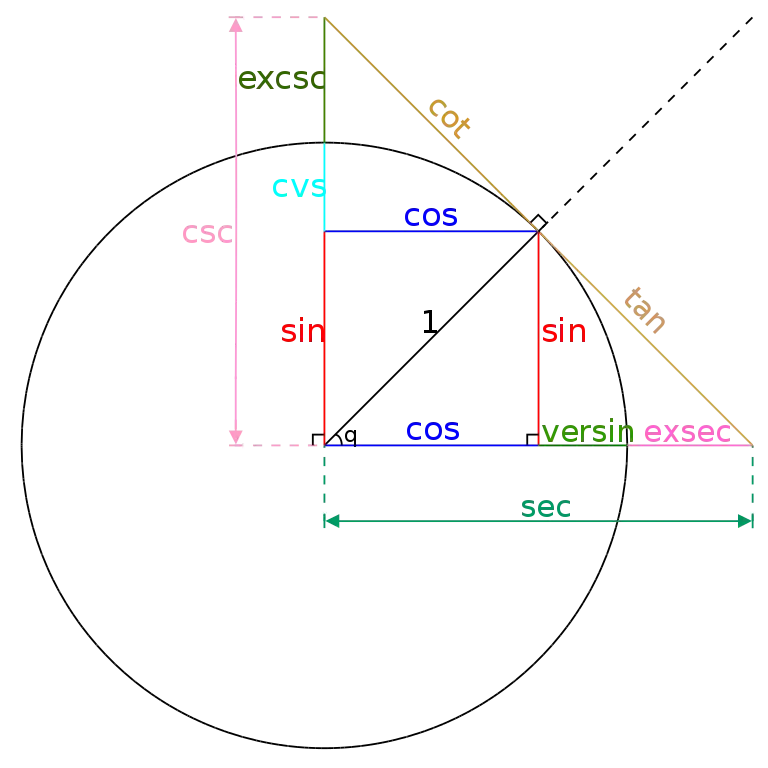
Históricamente, algunas funciones eran comunes, pero ahora rara vez se usan, como el acorde, el versine (que apareció en las primeras tablas), el coversine, el haversine, el exsecant y el excosecant. La lista de identidades trigonométricas muestra más relaciones entre estas funciones.

crd (θ) = 2 sin (θ / 2)
versin (θ) = 1 - cos (θ) = 2 sin (θ / 2)
coberturasin (θ) = 1 - sin (θ) = versión sin (π / 2 - θ)
haversin (θ) = 1/2 versin (θ ) = sin (θ / 2)
exsec(θ) = sec(θ) − 1
excsc (θ) = exsec (π / 2 - θ) = csc (θ) - 1

Etimología

La palabra seno deriva del latín sinus, que significa "curva; bahía", y más concretamente "el pliegue colgante de la parte superior de una toga", "el seno de una prenda", que se eligió como traducción de lo que se interpretó como la palabra árabe jaib, que significa "bolsillo" o "pliegue" en las traducciones del siglo XII de obras de Al-Battani y al-Khwārizmī al latín medieval. La elección se basó en una mala lectura de la forma escrita en árabe jyb (جيب), que a su vez se originó como una transliteración del sánscrito jīvā, que junto con su sinónimo jyā (el término sánscrito estándar para el seno) se traduce como "cuerda de arco", siendo a su vez adoptado del griego antiguo χορδή "cuerda".

La palabra tangente proviene del latín tangens que significa "tocar", ya que la línea toca el círculo de radio unidad, mientras que secante proviene del latín secans -"cortar"- ya que la línea corta al círculo.

El prefijo "co-" (en "coseno", "cotangente", "cosecante") se encuentra en el Canon triangulorum de Edmund Gunter (1620), que define el coseno como una abreviatura del sinus complementi (seno del ángulo complementario) y procede a definir los cotángens de manera similar.

Todas las funciones trigonométricas en un punto de la circunferencia

Te puede interesar
Icosaedro regular
(leer más)
Te puede interesar
Hiperplano
(leer más)
Te puede interesar
Diámetro
En geometría, un diámetro de un círculo es cualquier segmento de línea recta que pasa por el centro del círculo y cuyos extremos se encuentran en el... (leer más)
Más resultados...

seno ${displaystyle sin theta ={frac {mathrm {opuesto} }{mathrm {hipotenusa} }}}$	cosechar ${displaystyle csc theta ={frac {mathrm {hipotenusa} }{mathrm {opuesto} }}}$
coseno ${displaystyle cos theta ={frac {mathrm {adyacente} }{mathrm {hipotenusa} }}}$	secante ${displaystyle sec theta ={frac {mathrm {hipotenusa} }{mathrm {adyacente} }}}$
tangente $mostrar estilo de visualización tan theta = { frac { mathrm {opuesto} { mathrm {adyacente}}$	cotangente ${displaystyle cot theta ={frac {mathrm {adyacente} }{mathrm {opuesto} }}}$

Función	Descripción	Relación
usando radianes	usando grados
seno	opuesto / hipotenusa	$sin theta =cos left({frac {pi }{2}}-theta right)={frac {1}{csc theta }}$	${displaystyle sin x=cos left(90^{circ }-xright)={frac {1}{csc x}}}$
coseno	adyacente / hipotenusa	$cos theta =sin left({frac {pi }{2}}-theta right)={frac {1}{sec theta }},$	${displaystyle cos x=sin left(90^{circ }-xright)={frac {1}{sec x}},}$
tangente	opuesto / adyacente	$tan theta ={frac {sin theta }{cos theta }}=cot left({frac {pi }{2}}-theta right)={frac {1 {cottheta}}$	${displaystyle tan x={frac {sin x}{cos x}}=cot left(90^{circ }-xright)={frac {1}{cot x} }}$
cotangente	adyacente / opuesto	$cot theta ={frac {cos theta }{sin theta }}=tan left({frac {pi }{2}}-theta right)={frac {1 { bronceado theta}}$	${displaystyle cot x={frac {cos x}{sin x}}=tan left(90^{circ }-xright)={frac {1}{tan x} }}$
secante	hipotenusa / adyacente	$sec theta =csc left({frac {pi }{2}}-theta right)={frac {1}{cos theta }}$	${displaystyle sec x=csc left(90^{circ }-xright)={frac {1}{cos x}}}$
cosechar	hipotenusa / opuesto	$csc theta =sec left({frac {pi }{2}}-theta right)={frac {1}{sin theta }}$	${displaystyle csc x=sec left(90^{circ }-xright)={frac {1}{sin x}}}$