Función suave no analítica

En matemáticas, las funciones suaves (también llamadas funciones infinitamente diferenciables) y las funciones analíticas son dos tipos de funciones muy importantes. Se puede demostrar fácilmente que cualquier función analítica de un argumento real es fluida. Lo contrario no es cierto, como lo demuestra el contraejemplo siguiente.

Una de las aplicaciones más importantes de funciones suaves con soporte compacto es la construcción de los llamados suavizadores, que son importantes en teorías de funciones generalizadas, como la teoría de distribuciones de Laurent Schwartz.

La existencia de funciones suaves pero no analíticas representa una de las principales diferencias entre la geometría diferencial y la geometría analítica. En términos de la teoría de la gavilla, esta diferencia se puede expresar de la siguiente manera: la gavilla de funciones diferenciables en una variedad diferenciable está bien, en contraste con el caso analítico.

Las funciones siguientes se utilizan generalmente para construir particiones de unidad en variedades diferenciables.

Una función de ejemplo

Definición de la función

Considere la función

0,\0&{text{if }}xleq 0,end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">f()x)={}e− − 1xsix■0,0six≤ ≤ 0,{displaystyle f(x)={begin{cases}e^{-{frac {1}{x}} {text{if} }xleq 0,end{cases}0,\0&{text{if }}xleq 0,end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f44a0b0073f9c132d735fbdb2d25283158564868" style="vertical-align: -2.671ex; width:24.704ex; height:6.509ex;"/>

definido para cada número real x.

La función es fluida

La función f tiene derivadas continuas de todos los órdenes en cada punto x de la recta real. La fórmula para estas derivadas es

0,\0&{text{if }}xleq 0,end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">f()n)()x)={}pn()x)x2nf()x)six■0,0six≤ ≤ 0,{displaystyle f^{(n)}(x)={begin{cases}displaystyle {frac {frac {p_{n}(x^{2n}},f(x)}{text{if }x {0,}{if }xleq 0,end{cases}}}}}0,\0&{text{if }}xleq 0,end{cases}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/34c75f89d2aa3003732b97bfbbb39adef53f0129" style="vertical-align: -3.671ex; width:34.54ex; height:8.509ex;"/>

donde p_n(x) es un polinomio de grado n − 1 dado recursivamente por p₁(x) = 1 y

pn+1()x)=x2pn.()x)− − ()2nx− − 1)pn()x){displaystyle p_{n+1}(x)=x^{2}p_{n}'(x)-(2nx-1)p_{n}(x)}

para cualquier entero positivo n. A partir de esta fórmula, no queda completamente claro que las derivadas sean continuas en 0; esto se sigue del límite unilateral

limx↘ ↘ 0e− − 1xxm=0{displaystyle lim _{xsearrow ##{frac {e^{frac} {1} {x}}} {x} {}}=0}}} {cH0}}} {cH}}}}}}} {c}}}}}}}} {cH}}}}}}}} {cH}}}}}}}} {c}}}}}} {c}}}}}}}} {}}}}} {}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}} {}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}}}}}} {} {}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}

para cualquier entero no negativo m.

La función no es analítica

Como se vio anteriormente, la función f es suave y todas sus derivadas en el origen son 0. Por lo tanto, la serie de Taylor de f en el origen converge en todas partes a la función cero,

.. n=0JUEGO JUEGO f()n)()0)n!xn=.. n=0JUEGO JUEGO 0n!xn=0,x▪ ▪ R,{displaystyle sum _{n=0} {infty}{frac {f^{(n)} {n}{n}}x^{n}=sum ¿Qué? {0} {n}}x^{n}=0,qquad xin mathbb {R}

y entonces la serie de Taylor no es igual a f(x) para x > 0. En consecuencia, f no es analítico en el origen.

Funciones de transición suave

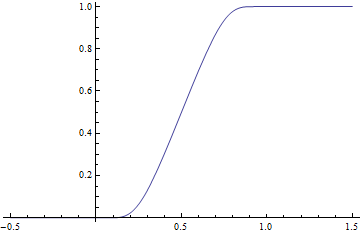
La función

g()x)=f()x)f()x)+f()1− − x),x▪ ▪ R,{displaystyle g(x)={frac {f(x)}{f(x)+f(1-x)}}qquad xin mathbb {R}

tiene un denominador estrictamente positivo en todas partes de la recta real, por lo tanto, g también es suave. Además, g(x) = 0 para x ≤ 0 y g(x) = 1 para x ≥ 1, por lo que proporciona una transición suave del nivel 0 al nivel 1 en el intervalo unitario [0, 1]. Para tener una transición suave en el intervalo real [a, b] con a < b, considere la función

R∋ ∋ x↦ ↦ g()x− − ab− − a).{displaystyle mathbb {R} ni xmapsto g{Bigl (}{frac {x-a}{b-a}{b-a}}{ Más grande.

Para números reales a < b < c < d, la función suave

R∋ ∋ x↦ ↦ g()x− − ab− − a)g()d− − xd− − c){displaystyle mathbb {R} ni xmapsto g{Bigl (}{frac {x-a}{b-a}{b-a}}{ Más grande. Más grande.

es igual a 1 en el intervalo cerrado [b, c] y desaparece fuera del intervalo abierto (a, d), por lo que puede servir como función de impacto.

Una función fluida que no es realmente analítica

Un ejemplo más patológico es una función infinitamente diferenciable que no es analítico en cualquier punto. Se puede construir por medio de una serie Fourier como sigue. Definir para todos x▪ ▪ R{displaystyle xin mathbb {R}

F()x):=.. k▪ ▪ Ne− − 2k#⁡ ⁡ ()2kx).{displaystyle F(x):=sum _{kin mathbb {N}e^{-{sqrt {2}}cos(2^{k}x).}

Desde la serie .. k▪ ▪ Ne− − 2k()2k)n{displaystyle sum _{kin mathbb {fn} {fn} {fn}}}} {fn}}}} {fn}}}}}}} {n}}}}}}} {fn}} {fn} {fn}}}}}}}}}}}}}} {n}}}}}}}}}} {n}} convergencias para todos n▪ ▪ N{displaystyle nin mathbb {N}, esta función se ve fácilmente como de clase C^JUEGO, por una aplicación inductiva estándar de la prueba Weierstrass M para demostrar convergencia uniforme de cada serie de derivados.

Ahora mostramos que F()x){displaystyle F(x)} no es analítico en cualquier múltiplo dyadic racional de π, es decir, en cualquier x:=π π ⋅ ⋅ p⋅ ⋅ 2− − q{displaystyle x:=picdot pcdot 2^{-q} con p▪ ▪ Z{displaystyle pin mathbb {Z} y q▪ ▪ N{displaystyle qin mathbb {N}. Desde la suma de la primera q{displaystyle q} términos es analítico, sólo necesitamos considerar q}(x)}" xmlns="http://www.w3.org/1998/Math/MathML">F■q()x){displaystyle F_{ títuloq}(x)}q}(x)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/73dbdaa6921d9069f12e3370cd1af8c7076e1167" style="vertical-align: -1.005ex; width:6.901ex; height:3.009ex;"/>, la suma de los términos con q}" xmlns="http://www.w3.org/1998/Math/MathML">k■q{displaystyle k]q}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9fdf1b63991086e94e8a7b183f9908eee528cdf8" style="vertical-align: -0.671ex; width:5.379ex; height:2.509ex;"/>. Para todas las órdenes de derivación n=2m{displaystyle n=2^{m} con m▪ ▪ N{displaystyle min mathbb {N}, m≥ ≥ 2{displaystyle mgeq 2} y q/2}" xmlns="http://www.w3.org/1998/Math/MathML">m■q/2{displaystyle m títuloq/2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f71c319c0b1c0a137f311f1aafc98d0b536ca079" style="vertical-align: -0.838ex; width:8.533ex; height:2.843ex;"/> tenemos

q}^{(n)}(x):=sum _{kin mathbb {N} atop k>q}e^{-{sqrt {2^{k}}}}{(2^{k})}^{n}cos(2^{k}x)=sum _{kin mathbb {N} atop k>q}e^{-{sqrt {2^{k}}}}{(2^{k})}^{n}geq e^{-n}n^{2n}quad (mathrm {as} ;nto infty)}" xmlns="http://www.w3.org/1998/Math/MathML">F■q()n)()x):=.. k▪ ▪ Nk■qe− − 2k()2k)n#⁡ ⁡ ()2kx)=.. k▪ ▪ Nk■qe− − 2k()2k)n≥ ≥ e− − nn2n()asn→ → JUEGO JUEGO ){displaystyle F_{fn]}(x):=sum _{kin mathbb {N} {fn} {fn} {fn}}{n}}}}}} {n}cos(2^{k}x)=sum _{kin mathbb {fn} {fn} {fn}} {fn}}} {fn} {fn}}}} {n}}}} {n}}}n}} {n}}} {n}}}} {n}}}}}n} {n}n}n}n}}}}}}}}}}}}}}}}}}}}n}n} {n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}}n}n}n}}n}n}n}n}n}n}n}n}n}n}n}n}n}n}}n}n}n}n}n}n}n}n}n}n}}n}n} e^{-n}n^{2n}quad (mathrm {as} ;nto infty)}q}^{(n)}(x):=sum _{kin mathbb {N} atop k>q}e^{-{sqrt {2^{k}}}}{(2^{k})}^{n}cos(2^{k}x)=sum _{kin mathbb {N} atop k>q}e^{-{sqrt {2^{k}}}}{(2^{k})}^{n}geq e^{-n}n^{2n}quad (mathrm {as} ;nto infty)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c5507e13f317b6cad4b039ba3bc7aa4505f5099d" style="vertical-align: -4.505ex; width:77.366ex; height:7.509ex;"/>

donde usamos el hecho de que #⁡ ⁡ ()2kx)=1{displaystyle cos(2^{k}x)=1} para todos 2^{q}}" xmlns="http://www.w3.org/1998/Math/MathML">2k■2q{displaystyle 2^{k} {q}}2^{q}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9bcab8b1eda10b4b70ea1b21e4e51f86279410df" style="vertical-align: -0.338ex; width:7.501ex; height:2.676ex;"/>, y atado la primera suma de abajo por el término con 2k=22m=n2{displaystyle 2^{k}=2m}=n^{2m}}. Como consecuencia de ello, x▪ ▪ R{displaystyle xin mathbb {R}

q}^{(n)}(x)|}{n!}}right)^{1/n}=+infty ,,}" xmlns="http://www.w3.org/1998/Math/MathML">lim supn→ → JUEGO JUEGO ()SilencioF■q()n)()x)Silencion!)1/n=+JUEGO JUEGO ,{displaystyle limsup _{nto infty }left({frac { imperf_{ Conf}^{(n)}(x)presivo}{n!}}right)^{1/n}=+infty ,}q}^{(n)}(x)|}{n!}}right)^{1/n}=+infty ,,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fa223a7ee95b25044b6688ef303c8e66071f527c" style="vertical-align: -3.505ex; width:32.281ex; height:8.843ex;"/>

para que el radio de convergencia de la serie Taylor q}}" xmlns="http://www.w3.org/1998/Math/MathML">F■q{displaystyle F_{ prendaq}q}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/43f4f7c02ea87dde7617f446874f5dd5bbc1c5c2" style="vertical-align: -1.005ex; width:3.762ex; height:2.843ex;"/> a x{displaystyle x} es 0 por la fórmula Cauchy-Hadamard. Puesto que el conjunto de la analítica de una función es un conjunto abierto, y dado que los racionales dyadicos son densos, concluimos que q}}" xmlns="http://www.w3.org/1998/Math/MathML">F■q{displaystyle F_{ prendaq}q}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/43f4f7c02ea87dde7617f446874f5dd5bbc1c5c2" style="vertical-align: -1.005ex; width:3.762ex; height:2.843ex;"/>, y por lo tanto F{displaystyle F}, no es nada analítico en R{displaystyle mathbb {R}.

Aplicación a la serie de Taylor

Para cada secuencia α₀, α₁, α₂,... de números reales o complejos, la siguiente construcción muestra la existencia de una función suave F sobre la recta real que tiene estos números como derivadas en el origen. En particular, cada secuencia de números puede aparecer como coeficientes de la serie de Taylor de una función suave. Este resultado se conoce como lema de Borel, en honor a Émile Borel.

Con la función de transición suave g como arriba, defina

h()x)=g()2+x)g()2− − x),x▪ ▪ R.{displaystyle h(x)=g(2+x),g(2-x),qquad xin mathbb {R}.}

Esta función h también es fluida; es igual a 1 en el intervalo cerrado [−1,1] y desaparece fuera del intervalo abierto (−2,2). Usando h, defina para cada número natural n (incluido el cero) la función suave

↑ ↑ n()x)=xnh()x),x▪ ▪ R,{displaystyle psi _{n}(x)=x^{n},h(x),qquad xin mathbb {R}

que concuerda con el monomio xⁿ en [−1,1] y desaparece fuera del intervalo (−2,2). Por lo tanto, la k-ésima derivada de ψ_n en el origen satisface

↑ ↑ n()k)()0)={}n!sik=n,0de lo contrario,k,n▪ ▪ N0,{displaystyle psi _{(k)}(0)={begin{cases}n! } k=n, âtext{otherwise,}end{cases}quad k,nin mathbb {N}

y el teorema de acotación implica que ψ_n y cada derivada de ψ_n está acotada. Por lo tanto, las constantes

λ λ n=max{}1,Silencioα α nSilencio,.. ↑ ↑ n.. JUEGO JUEGO ,.. ↑ ↑ n()1).. JUEGO JUEGO ,...... ,.. ↑ ↑ n()n).. JUEGO JUEGO },n▪ ▪ N0,{displaystyle lambda _{n}=max {bigl{}1, soportealpha ¿Qué? {N} _{0},}

que involucran la norma suprema de ψ_n y sus primeras n derivadas, son números reales bien definidos. Definir las funciones escaladas.

fn()x)=α α nn!λ λ nn↑ ↑ n()λ λ nx),n▪ ▪ N0,x▪ ▪ R.{displaystyle f_{n}(x)={frac {fnMicrosoft} ¿Por qué? {N} _{0},;xin mathbb {R}

Mediante la aplicación repetida de la regla de la cadena,

fn()k)()x)=α α nn!λ λ nn− − k↑ ↑ n()k)()λ λ nx),k,n▪ ▪ N0,x▪ ▪ R,{displaystyle f_{(k)}(x)={frac {alpha ¡No! lambda ¿Por qué?

y, usando el resultado anterior para la k-ésima derivada de ψ_n en cero,

fn()k)()0)={}α α nsik=n,0de lo contrario,k,n▪ ▪ N0.{displaystyle f_{(k)}(0)={begin{cases}alpha ################################################################################################################################################################################################################################################################ } k=n, âtext{otherwise,}end{cases}qquad k,nin mathbb No.

Queda por demostrar que la función

F()x)=.. n=0JUEGO JUEGO fn()x),x▪ ▪ R,{displaystyle F(x)=sum _{n=0}{infty }f_{n}(x),qquad xin mathbb {R}

está bien definido y se puede diferenciar término por término infinitas veces. Para ello observe que por cada k

<math alttext="{displaystyle sum _{n=0}^{infty }|f_{n}^{(k)}|_{infty }leq sum _{n=0}^{k+1}{frac {|alpha _{n}|}{n!,lambda _{n}^{n-k}}}|psi _{n}^{(k)}|_{infty }+sum _{n=k+2}^{infty }{frac {1}{n!}}underbrace {frac {1}{lambda _{n}^{n-k-2}}} _{leq ,1}underbrace {frac {|alpha _{n}|}{lambda _{n}}} _{leq ,1}underbrace {frac {|psi _{n}^{(k)}|_{infty }}{lambda _{n}}} _{leq ,1}.. n=0JUEGO JUEGO .. fn()k).. JUEGO JUEGO ≤ ≤ .. n=0k+1Silencioα α nSilencion!λ λ nn− − k.. ↑ ↑ n()k).. JUEGO JUEGO +.. n=k+2JUEGO JUEGO 1n!1λ λ nn− − k− − 2⏟ ⏟ ≤ ≤ 1Silencioα α nSilencioλ λ n⏟ ⏟ ≤ ≤ 1.. ↑ ↑ n()k).. JUEGO JUEGO λ λ n⏟ ⏟ ≤ ≤ 1.JUEGO JUEGO ,{displaystyle sum _{n=0} {infty }f_{n}fn}fn_{infty }leq sum _{n=0}{k+1}{frac {fnMicrosoft Sans Serif} _{n}{n!, lambda _{n} {fn}fn}fn}fnn}fnnnnnnnn}fnnnnnnnnn}nnnnnnnnnnnnn}nnnnnnnnnnnnnnnn}nnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn}\nnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn\\\\\\\ }{frac {1}{n}}underbrace {frac {1}{lambda ¿Qué? ¿Por qué? ¿Por qué? ¿Qué? - ¿Qué?<img alt="sum _{{n=0}}^{infty }|f_{n}^{{(k)}}|_{infty }leq sum _{{n=0}}^{{k+1}}{frac {|alpha _{n}|}{n!,lambda _{n}^{{n-k}}}}|psi _{n}^{{(k)}}|_{infty }+sum _{{n=k+2}}^{infty }{frac 1{n!}}underbrace {{frac 1{lambda _{n}^{{n-k-2}}}}}_{{leq ,1}}underbrace {{frac {|alpha _{n}|}{lambda _{n}}}}_{{leq ,1}}underbrace {{frac {|psi _{n}^{{(k)}}|_{infty }}{lambda _{n}}}}_{{leq ,1}}

donde la serie infinita restante converge según la prueba de razón.

Aplicación a dimensiones superiores

Para cada radio r > 0,

Rn∋ ∋ x↦ ↦ Ψ Ψ r()x)=f()r2− − .. x.. 2){displaystyle mathbb {R} ^{n}ni xmapsto Psi _{r}(x)=f(r^{2}- eternax^{2}

con la norma Euclideanxtención permanente define una función suave en n-dimensional Espacio euclidiano con soporte en la bola de radio r, pero 0}" xmlns="http://www.w3.org/1998/Math/MathML">Ψ Ψ r()0)■0{displaystyle Psi _{r}(0)}0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/42c11d1296dca30609c25b7edd47e77abe51da05" style="vertical-align: -0.838ex; width:10.015ex; height:2.843ex;"/>.

Análisis complejo

Esta patología no puede ocurrir con funciones diferenciables de una variable compleja en lugar de una variable real. De hecho, todas las funciones holomorfas son analíticas, de modo que el hecho de que la función f definida en este artículo no sea analítica a pesar de ser infinitamente diferenciable es una indicación de una de las diferencias más dramáticas entre las funciones holomorfas. análisis de variables y de variables complejas.

Tenga en cuenta que aunque la función f tiene derivadas de todos los órdenes sobre la línea real, la continuación analítica de f de la media línea positiva x > 0 al plano complejo, es decir, la función

C∖ ∖ {}0}∋ ∋ z↦ ↦ e− − 1z▪ ▪ C,{displaystyle mathbb {C} setminus {0}ni zmapsto e^{-{frac {1}{z}}}in mathbb {C}} {} {}}} {}} {}}} {}}} {}}}} {}}}}}} {

tiene una singularidad esencial en el origen y, por lo tanto, ni siquiera es continuo, y mucho menos analítico. Según el gran teorema de Picard, alcanza todos los valores complejos (con excepción de cero) infinitas veces en cada vecindad del origen.