Función de cantor

Ajustar Compartir Imprimir Citar

Función continua que no es absolutamente continua

El gráfico de la función Cantor en el intervalo de unidad

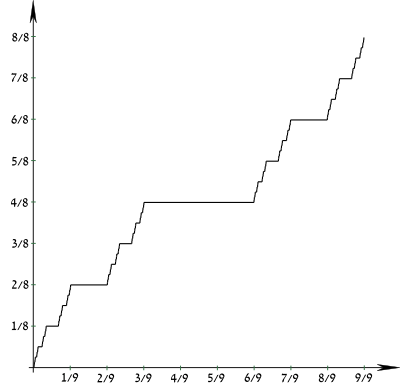
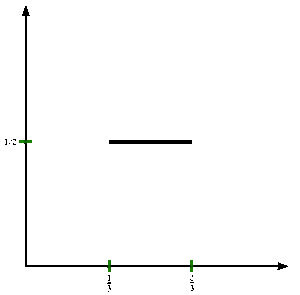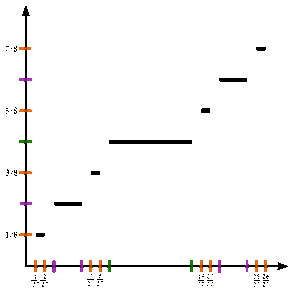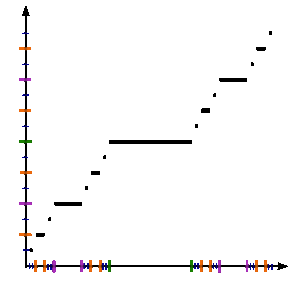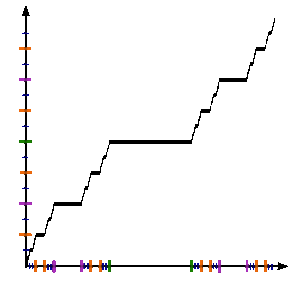
En matemáticas, la función de Cantor es un ejemplo de una función que es continua, pero no absolutamente continua. Es un contraejemplo notorio en el análisis, porque desafía las intuiciones ingenuas sobre la continuidad, la derivada y la medida. Aunque es continua en todas partes y tiene derivada cero en casi todas partes, su valor aún va de 0 a 1 a medida que su argumento va de 0 a 1. Por lo tanto, en un sentido, la función se parece mucho a una constante que no puede crecer, y en otro, de hecho crece monótonamente.

También se le llama la función ternaria de Cantor, la función de Lebesgue, la función singular de Lebesgue, la función de Cantor –Función Vitali, la escalera del diablo, la función escalera de Cantor y la función Cantor–Lebesgue. Georg Cantor (1884) introdujo la función de Cantor y mencionó que Scheeffer señaló que era un contraejemplo de una extensión del teorema fundamental del cálculo planteado por Harnack. La función de Cantor fue discutida y popularizada por Scheeffer (1884), Lebesgue (1904) y Vitali (1905).

Definición

Para definir la función Cantor ${displaystyle c:[0,1]to [0,1]}$ , vamos $x$ ser cualquier número en $[0,1]$ y obtener $c(x)$ por los siguientes pasos:

Express $x$ en la base 3.
Si la representación de base-3 $x$ contiene un 1, reemplazar cada dígito estrictamente después del primero 1 por 0.
Reemplazar los 2s restantes con 1s.
Interpretar el resultado como un número binario. El resultado es $c(x)$ .

Por ejemplo:

${tfrac {1}{4}}$ tiene la representación ternaria 0.02020202... No hay 1s por lo que la siguiente etapa es todavía 0.02020202... Esto es reescrito como 0.01010101... Esta es la representación binaria ${tfrac {1}{3}}$ Así que ${displaystyle c({tfrac {1}{4}})={tfrac {1}{3}}}$ .
${tfrac {1}{5}}$ tiene la representación ternaria 0.01210121... Los dígitos después del primer 1 son reemplazados por 0s para producir 0.01000000... Esto no es reescrito ya que no tiene 2s. Esta es la representación binaria ${tfrac {1}{4}}$ Así que ${displaystyle c({tfrac {1}{5}})={tfrac {1}{4}}}$ .
${displaystyle {tfrac {200}{243}}}$ tiene la representación ternaria 0.21102 (o 0.211012222...). Los dígitos después del primer 1 son reemplazados por 0s para producir 0.21. Esto es reescrito como 0.11. Esta es la representación binaria ${tfrac 34}$ Así que ${displaystyle c({tfrac {200}{243}})={tfrac {3}{4}}}$ .

Equivalentemente, si ${mathcal {C}}$ es el Cantor establecido en [0,1], luego la función Cantor ${displaystyle c:[0,1]to [0,1]}$ puede definirse como

{displaystyle c(x)={begin{cases}sum _{n=1}^{infty }{frac {a_{n}}{2^{n}}},&x=sum _{n=1}^{infty }{frac {2a_{n}}{3^{n}}}in {mathcal {C}} mathrm {for} a_{n}in {0,1};\sup _{yleq x,,yin {mathcal {C}}}c(y),&xin [0,1]smallsetminus {mathcal {C}}.end{cases}}}

Esta fórmula está bien definida, ya que cada miembro del conjunto Cantor tiene un único base 3 representación que sólo contiene los dígitos 0 o 2. (Para algunos miembros de ${mathcal {C}}$ , la expansión ternaria está repitiendo con el seguimiento de 2's y hay una alternativa de expansión no recurrente que termina en 1. Por ejemplo, ${tfrac {1}{3}}$ = 0,1₃ = 0,02222...₃ es miembro del conjunto Cantor). Desde ${displaystyle c(0)=0}$ y ${displaystyle c(1)=1}$ , y $c$ es monotónico en ${mathcal {C}}$ , está claro que ${displaystyle 0leq c(x)leq 1}$ también tiene para todos ${displaystyle xin [0,1]smallsetminus {mathcal {C}}}$ .

Propiedades

La función Cantor desafía intuiciones ingenuas acerca de la continuidad y la medida; aunque es continua en todas partes y tiene cero derivado casi en todas partes, ${textstyle c(x)}$ va de 0 a 1 ${textstyle x}$ va de 0 a 1, y toma cada valor en entre. La función Cantor es el ejemplo más frecuentemente citado de una función real que es uniformemente continua (precisamente, es Hölder continuo de exponente α= log 2/log 3) pero no absolutamente continuo. Es constante en intervalos de la forma (0.x₁x₂x₃...x_n022222..., 0.x₁x₂x₃...x_n200000...), y cada punto no en el conjunto Cantor está en uno de estos intervalos, por lo que su derivado es 0 fuera del conjunto Cantor. Por otro lado, no tiene derivado en ningún punto en un subconjunto incontable del conjunto Cantor que contiene los puntos finales de intervalo descritos anteriormente.

La función Cantor también se puede ver como la función de distribución de probabilidad acumulada de la medida 1/2-1/2-1/2 Bernoulli μ apoyado en el conjunto Cantor: ${textstyle c(x)=mu ([0,x])}$ . Esta distribución de probabilidad, llamada distribución Cantor, no tiene parte discreta. Es decir, la medida correspondiente es atomless. Es por eso que no hay discontinuidades de salto en la función; cualquier salto de este tipo correspondería a un átomo en la medida.

Sin embargo, ninguna parte no constante de la función de Cantor se puede representar como una integral de una función de densidad de probabilidad; la integración de cualquier función de densidad de probabilidad putativa que no sea cero en casi todas partes en cualquier intervalo dará una probabilidad positiva a algún intervalo al que esta distribución asigna probabilidad cero. En particular, como señaló Vitali (1905), la función no es la integral de su derivada, aunque la derivada existe en casi todas partes.

La función de Cantor es el ejemplo estándar de una función singular.

La función Cantor no disminuye, por lo que en particular su gráfico define una curva rectificable. Scheeffer (1884) mostró que la longitud del arco de su gráfico es 2. Tenga en cuenta que el gráfico de cualquier función de nodecreación tal que $f(0)=0$ y $f(1)=1$ tiene longitud no superior a 2. En este sentido, la función Cantor es extremal.

Falta de continuidad absoluta

Debido a que la medida de Lebesgue del conjunto incontablemente infinito de Cantor es 0, para cualquier ε < 1 y δ, existe una secuencia finita de subintervalos separados por parejas con longitud total < δ sobre el cual la función de Cantor aumenta acumulativamente más que ε.

De hecho, para todos δ> 0 hay finitamente muchos intervalos de unión pares (x_k,Sí._k) (1 ≤k≤MCon $<math alttext="{displaystyle sum limits _{k=1}^{M}(y_{k}-x_{k}).. k=1M()Sí.k− − xk).δ δ {displaystyle sum limits ¿Qué? }<img alt="{displaystyle sum limits _{k=1}^{M}(y_{k}-x_{k})$ y ${displaystyle sum limits _{k=1}^{M}(c(y_{k})-c(x_{k}))=1}$ .

Definiciones alternativas

Construcción iterativa

A continuación definimos una secuencia {f_n} de funciones en el intervalo unitario que converge a la función de Cantor.

Sea f₀(x) = x.

Entonces, para cada entero n ≥ 0, la siguiente función f_n+1(x) se definirá en términos de f_n(x) de la siguiente manera:

Sea f_n+1(x) = 1/ 2 × f_n(3x), cuando 0 ≤ x ≤ 1/3 ;

Sea f_n+1(x) = 1/2, cuando 1/3 ≤ x ≤ 2/3 ;

Sea f_n+1(x) = 1/ 2 + 1/2 × f_n(3 x − 2), cuando 2/3 ≤ x ≤ 1.

Las tres definiciones son compatibles en los extremos 1/3 y 2/3, porque f_n(0) = 0 y f_n(1) = 1 para cada n, por inducción. Se puede comprobar que f_n converge puntualmente a la función de Cantor definida anteriormente. Además, la convergencia es uniforme. En efecto, separando en tres casos, según la definición de f_n+1, se ve que

max_{x in [0, 1]} |f_{n+1}(x) - f_n(x)| le frac 1 2 , max_{x in [0, 1]} |f_{n}(x) - f_{n-1}(x)|, quad n ge 1.

Si f denota la función límite, se sigue que, para cada n ≥ 0,

max_{x in [0, 1]} |f(x) - f_n(x)| le 2^{-n+1} , max_{x in [0, 1]} |f_1(x) - f_0(x)|.

Tampoco importa la elección de la función de inicio, siempre que f₀(0) = 0, f₀(1) = 1 y f₀ está acotado.

Volumen fractal

La función Cantor está estrechamente relacionada con el conjunto Cantor. El conjunto Cantor C puede definirse como el conjunto de esos números en el intervalo [0, 1] que no contienen el dígito 1 en su expansión base-3 (trídica), excepto si el 1 es seguido por ceros solamente (en cuyo caso la cola 1000 $ldots$ puede ser reemplazado por 0222 $ldots$ para deshacerse de cualquier 1). Resulta que el conjunto Cantor es un fractal con (incontablemente) infinitamente muchos puntos (volumen dimensional), pero la longitud cero (volumen dimensional). Sólo el D- volumen dimensional $H_D$ (en el sentido de una Medida Hausdorff) toma un valor finito, donde $D = log(2)/log(3)$ es la dimensión fractal de C. Podemos definir la función Cantor alternativamente como la D- volumen dimensional de secciones del conjunto Cantor

f(x)=H_D(C cap (0,x)).

Autosimilitud

La función Cantor posee varias simetrías. Para $0leq xleq 1$ , hay una simetría de reflexión

{displaystyle c(x)=1-c(1-x)}

y un par de aumentos, uno a la izquierda y otro a la derecha:

{displaystyle cleft({frac {x}{3}}right)={frac {c(x)}{2}}}

{displaystyle cleft({frac {x+2}{3}}right)={frac {1+c(x)}{2}}}

Los aumentos se pueden conectar en cascada; generan el monoide diádico. Esto se muestra definiendo varias funciones auxiliares. Definir la reflexión como

{displaystyle r(x)=1-x}

La primera autosimetría se puede expresar como

{displaystyle rcirc c=ccirc r}

donde el símbolo $circ$ denota la composición de la función. Eso es, ${displaystyle (rcirc c)(x)=r(c(x))=1-c(x)}$ y también para los otros casos. Para las magnificaciones izquierda y derecha, escriba los mapas izquierdos

{displaystyle L_{D}(x)={frac {x}{2}}}

{displaystyle L_{C}(x)={frac {x}{3}}}

Entonces la función de Cantor obedece

{displaystyle L_{D}circ c=ccirc L_{C}}

Del mismo modo, defina las asignaciones correctas como

{displaystyle R_{D}(x)={frac {1+x}{2}}}

{displaystyle R_{C}(x)={frac {2+x}{3}}}

Entonces, igualmente,

{displaystyle R_{D}circ c=ccirc R_{C}}

Los dos lados se pueden reflejar uno sobre el otro, en ese

{displaystyle L_{D}circ r=rcirc R_{D}}

y del mismo modo,

{displaystyle L_{C}circ r=rcirc R_{C}}

Estas operaciones pueden apilarse arbitrariamente. Considere, por ejemplo, la secuencia de movimientos de derecha izquierda ${displaystyle LRLLR.}$ Añadiendo los subscriptos C y D, y, para claridad, bajando el operador de composición $circ$ en todos menos algunos lugares, uno tiene:

{displaystyle L_{D}R_{D}L_{D}L_{D}R_{D}circ c=ccirc L_{C}R_{C}L_{C}L_{C}R_{C}}

Arbitrary finite-length strings in the letters L and R correspond to the dyadic rationals, in that every dyadic rational can be written as both ${displaystyle y=n/2^{m}}$ para entero n y m y como longitud finita de bits ${displaystyle y=0.b_{1}b_{2}b_{3}cdots b_{m}}$ con ${displaystyle b_{k}in {0,1}.}$ Así, cada racional dyadico está en correspondencia única con alguna simetría de la función Cantor.

Algunas reorganizaciones notacionales pueden hacer que la anterior sea ligeramente más fácil de expresar. Vamos $g_{0}$ y $g_{1}$ soporte para L y R. La composición de la función extiende esto a un monoide, en que uno puede escribir ${displaystyle g_{010}=g_{0}g_{1}g_{0}}$ y en general, ${displaystyle g_{A}g_{B}=g_{AB}}$ para algunas cadenas binarias de dígitos A, B, donde AB es sólo la concatenación ordinaria de tales cuerdas. El monoide dyadic M es entonces el monoide de todos esos movimientos de izquierda de longitud finita. Escritura ${displaystyle gamma in M}$ como elemento general del monoide, hay una simetría correspondiente de la función Cantor:

{displaystyle gamma _{D}circ c=ccirc gamma _{C}}

El monoide dyadic tiene varias propiedades interesantes. Se puede ver como un número finito de izquierda-derecha se mueve por un árbol binario infinito; las "levas" infinitamente distantes en el árbol corresponden a los puntos en el conjunto de Cantor, y por lo tanto, el monoide también representa las simetrías del conjunto de Cantor. De hecho, una gran clase de fractales comúnmente presentes son descritos por el monoide dyadic; ejemplos adicionales se pueden encontrar en el artículo sobre curvas de Rham. Otros fractales que poseen auto-similaridad se describen con otros tipos de monoides. El monoide dyadic es en sí mismo un submonoide del grupo modular ${displaystyle SL(2,mathbb {Z}).}$

Tenga en cuenta que la función de Cantor tiene más que un parecido pasajero con la función de signo de interrogación de Minkowski. En particular, obedece exactamente a las mismas relaciones de simetría, aunque de forma alterada.

Generalizaciones

Dejar

y=sum_{k=1}^infty b_k 2^{-k}

sea la expansión diádica (binaria) del número real 0 ≤ y ≤ 1 en términos de dígitos binarios b_k ∈ {0,1}. Esta expansión se analiza con mayor detalle en el artículo sobre la transformación diádica. Luego considere la función

C_z(y)=sum_{k=1}^infty b_k z^{k}.

Para z = 1/3, el inverso de la función x = 2 C_1/3 (y) es la función de Cantor. Es decir, y = y(x) es la función de Cantor. En general, para cualquier z < 1/2, C_z(y) se parece a la función de Cantor volteada, con el ancho de los pasos que se ensanchan a medida que z se aproxima a cero.

Como se mencionó anteriormente, la función Cantor es también la función de distribución acumulativa de una medida en el conjunto Cantor. Diferentes funciones Cantor, o las escaleras del diablo, se pueden obtener considerando diferentes medidas de probabilidad sin átomos apoyadas en el conjunto Cantor u otros fractales. Mientras que la función Cantor tiene derivado 0 casi por todas partes, la investigación actual se centra en la cuestión del tamaño del conjunto de puntos donde el derivado derecho superior es distinto del derivado derecho inferior, causando que el derivado no exista. Este análisis de diferenciabilidad generalmente se da en términos de dimensión fractal, con la dimensión Hausdorff la opción más popular. Esta línea de investigación fue iniciada en los años noventa por Darst, quien mostró que la dimensión Hausdorff del conjunto de la no diferenciabilidad de la función Cantor es el cuadrado de la dimensión del conjunto Cantor, ${displaystyle (log 2/log 3)^{2}}$ . Posteriormente Falconer mostró que esta relación escatimadora mantiene para todas las medidas regulares y singulares de Ahlfor, es decir.

{displaystyle dim _{H}left{x:f'(x)=lim _{hto 0^{+}}{frac {mu ([x,x+h])}{h}}{text{ does not exist}}right}=left(dim _{H}operatorname {supp} (mu)right)^{2}}

La función de signo de interrogación de Hermann Minkowski se parece vagamente a la función de Cantor visualmente, aparece como una función "suavizada" forma de este último; se puede construir pasando de una expansión en fracción continua a una expansión binaria, al igual que la función de Cantor se puede construir pasando de una expansión ternaria a una expansión binaria. La función de signo de interrogación tiene la propiedad interesante de tener derivadas que se desvanecen en todos los números racionales.