Función sigmoidea

La curva logística

Parcela de la función de error

Una función sigmoidea es una función matemática que tiene una característica curva en forma de "S" o curva sigmoidea.

Un ejemplo común de una función sigmoidea es la función logística que se muestra en la primera figura y se define mediante la fórmula:

S()x)=11+e− − x=exex+1=1− − S()− − x).{displaystyle S(x)={1}{1+e^{-x}={frac {e^{x}{e^{x}+1}=1-S(-x).}

En la sección de ejemplos se proporcionan otras funciones sigmoideas estándar. En algunos campos, sobre todo en el contexto de las redes neuronales artificiales, el término "función sigmoidea" se utiliza como un alias para la función logística.

Los casos especiales de la función sigmoidea incluyen la curva de Gompertz (utilizada en sistemas de modelado que se saturan con valores grandes de x) y la curva conopial (utilizada en el aliviadero de algunas presas). Las funciones sigmoideas tienen el dominio de todos los números reales, con un valor de retorno (respuesta) que suele aumentar de forma monótona pero podría disminuir. Las funciones sigmoideas suelen mostrar un valor de retorno (eje y) en el rango de 0 a 1. Otro rango de uso común es de −1 a 1.

Se ha utilizado una amplia variedad de funciones sigmoideas, incluidas las funciones de tangente hiperbólica y logística, como función de activación de las neuronas artificiales. Las curvas sigmoideas también son comunes en estadística como funciones de distribución acumulativa (que van de 0 a 1), como las integrales de la densidad logística, la densidad normal y las funciones de densidad de probabilidad t de Student. La función logística sigmoidea es invertible y su inversa es la función logit.

Definición

Una función sigmoidea es una función real diferenciable y acotada que se define para todos los valores de entrada reales y tiene una derivada no negativa en cada punto y exactamente un punto de inflexión. Una "función" sigmoide y una "curva" sigmoidea referirse al mismo objeto.

Propiedades

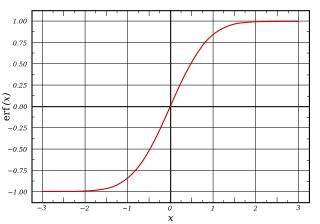
En general, una función sigmoidea es monótona y tiene una primera derivada que tiene forma de campana. Por el contrario, la integral de cualquier función continua, no negativa, en forma de campana (con un máximo local y ningún mínimo local, a menos que degenere) será sigmoidal. Por lo tanto, las funciones de distribución acumulativa para muchas distribuciones de probabilidad comunes son sigmoidales. Un ejemplo de ello es la función de error, que está relacionada con la función de distribución acumulativa de una distribución normal; otra es la función arctan, que está relacionada con la función de distribución acumulativa de una distribución de Cauchy.

Una función sigmoide es limitada por un par de asintotos horizontales como x→ → ± ± JUEGO JUEGO {displaystyle xrightarrow pm infty }.

Una función sigmoidea es convexa para valores menores que un punto en particular, y es cóncava para valores mayores que ese punto: en muchos de los ejemplos aquí, ese punto es 0.

Ejemplos

Se compararon algunas funciones de sigmoide. En el dibujo todas las funciones se normalizan de tal manera que su pendiente en el origen es 1.

• Función logística
  f()x)=11+e− − x{displaystyle f(x)={1+e^{-x}}

  
• Tangente hiperbólico (versión rota y escalada de la función logística, arriba)
  f()x)=Tanh⁡ ⁡ x=ex− − e− − xex+e− − x{displaystyle f(x)=tanh x={frac {e^{x}-e^{-x}{e^{x}+e^{-x}}}}

  
• Función dictaminatoria
  f()x)=arctan⁡ ⁡ x{displaystyle f(x)=arctan x}

  
• Función gudermanniana
  f()x)=gd⁡ ⁡ ()x)=∫ ∫ 0xdtcosh⁡ ⁡ t=2arctan⁡ ⁡ ()Tanh⁡ ⁡ ()x2)){displaystyle f(x)=fnMicroc {fnMicroc {f} {fnMicroc}=2arctanleft(tanhleft({frac {x}right)}}}}}right)}}}}derecho)}

  
• Función de error
  f()x)=er⁡ ⁡ ()x)=2π π ∫ ∫ 0xe− − t2dt{displaystyle f(x)=operatorname {erf} (x)={frac {2}{sqrt {pi}}int} {fn}} {fn}} {fn}} {fn}} {fn}}}} {fn}}} {fn}}} {fn}}}} {f}}}} {f}}}}} {f}}}}}}} { ¿Qué?

  
• Función logística generalizada
  0}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">f()x)=()1+e− − x)− − α α ,α α ■0{displaystyle f(x)=left(1+e^{-x}right)^{-alpha },quad alpha }

  0}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fd1cdd88719b29777a0f156de814f924f7c86e80" style="vertical-align: -1.005ex; width:28.851ex; height:3.509ex;"/>
• Función de movimiento
  f()x)={}()∫ ∫ 01()1− − u2)Ndu)− − 1∫ ∫ 0x()1− − u2)Ndu,SilencioxSilencio≤ ≤ 1Sgn⁡ ⁡ ()x)SilencioxSilencio≥ ≥ 1N▪ ▪ Z≥ ≥ 1{displaystyle f(x)={begin{cases}{displaystyle left(int ¿Por qué? ¿Por qué? Nin mathbb {Z} geq 1}

  
• Algunas funciones algebraicas, por ejemplo
  f()x)=x1+x2{displaystyle f(x)={frac {x}{sqrt {1+x^{2}}}}

  
• y en forma más general
  f()x)=x()1+SilencioxSilenciok)1/k{displaystyle f(x)={frac {x}{left(1+Sobrevivirx^{k}right)^{1/k}}}}

  
• Hasta turnos y escalas, muchos sigmoides son casos especiales de
  f()x)=φ φ ()φ φ ()x,β β ),α α ),{displaystyle f(x)=varphi (varphi (x,beta),alpha),}

  
  Donde
  φ φ ()x,λ λ )={}()1− − λ λ x)1/λ λ λ λ ل ل 0e− − xλ λ =0{displaystyle varphi (x,lambda)={begin{cases}(1-lambda x)^{1/lambda } {lambdaneq 0\e^{-x} limitlambda =0\end{cases}}}}}}}

  
  es el inverso de la transformación negativa de Box–Cox, y <math alttext="{displaystyle alpha α α .1{displaystyle alpha.<img alt="alpha y <math alttext="{displaystyle beta β β .1{displaystyle beta.<img alt="beta son parámetros de forma.
• Interpolación de Smooth normalizada a (-1,1) y n{displaystyle n} es la pendiente a cero:

Aplicaciones

Logística invertida S-curve para modelar la relación entre el rendimiento del trigo y la salinidad del suelo.

Muchos procesos naturales, como los de las curvas de aprendizaje de sistemas complejos, exhiben una progresión desde pequeños comienzos que se acelera y se acerca a un clímax con el tiempo. Cuando falta un modelo matemático específico, a menudo se usa una función sigmoidea.

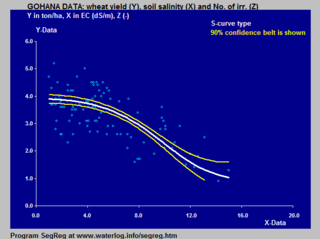
El modelo de van Genuchten-Gupta se basa en una curva S invertida y se aplica a la respuesta del rendimiento de los cultivos a la salinidad del suelo.

Los ejemplos de la aplicación de la curva S logística a la respuesta del rendimiento del cultivo (trigo) tanto a la salinidad del suelo como a la profundidad del nivel freático en el suelo se muestran en el modelado de la respuesta del cultivo en la agricultura.

En las redes neuronales artificiales, a veces se utilizan funciones no uniformes para mejorar la eficiencia; estos se conocen como sigmoides duros.

En el procesamiento de señales de audio, las funciones sigmoideas se utilizan como funciones de transferencia de modelador de ondas para emular el sonido del recorte de circuitos analógicos.

En bioquímica y farmacología, las ecuaciones de Hill y Hill-Langmuir son funciones sigmoideas.

En los gráficos por computadora y la representación en tiempo real, algunas de las funciones sigmoideas se utilizan para combinar colores o geometría entre dos valores, sin problemas y sin costuras ni discontinuidades visibles.

Las curvas de titulación entre ácidos fuertes y bases fuertes tienen forma sigmoidea debido a la naturaleza logarítmica de la escala de pH.

La función logística se puede calcular de manera eficiente utilizando Unums de tipo III.